
| Afaceri | Agricultura | Comunicare | Constructii | Contabilitate | Contracte |
| Economie | Finante | Management | Marketing | Transporturi |
Finante
|
|
Qdidactic » bani & cariera » finante Scurte consideratii asupra factorilor de productie si a functiei de productie |
Scurte consideratii asupra factorilor de productie si a functiei de productie
Scurte consideratii asupra factorilor de productie si a functiei de productie
In mod sintetic,
prin genericul de factori de productie se intelege ansamblul
mijloacelor participante la activitatea productiva. Este evident ca
numarul mijloacelor participante la activitatea de productie este
dependent de complexitatea acestuia. Din acest motiv vom considera in mod
formal ca daca numarul mijloacelor de productie este n,
atunci ansamblul mijloacelor de productie va fi o submultime ![]() . In mod uzual se considera
. In mod uzual se considera ![]() in baza
observatiei ca mijloacele de productie nu pot lua decat valori
negative.
in baza
observatiei ca mijloacele de productie nu pot lua decat valori
negative.
Prin functie
de productie se intelege practic orice functie ![]() care indeplineste
anumite cerinte impuse de specificul activitatii productive:
care indeplineste
anumite cerinte impuse de specificul activitatii productive:
1) Functia de productie este o functie continua
Aceasta
restrictie se refera la faptul ca variatii mici ale
factorilor de productie nu modifica semnificativ volumul
productiei. Din punct de vedere matematic aceasta inseamna ca
daca vom nota ![]() factorii de
productie si cu
factorii de
productie si cu ![]() variatia
acestora, atunci
variatia
acestora, atunci
![]()
cu conditia ca ![]() sa fie suficient
de mici.
sa fie suficient
de mici.
2) Factorii de productie sunt strict necesari
Aceasta
cerinta se refera la faptul ca daca vectorul de
productie ![]() are cel putin o
componenta nula atunci volumul productiei este de asemenea nul.
are cel putin o
componenta nula atunci volumul productiei este de asemenea nul.
De exemplu,
daca ![]() , atunci
, atunci ![]() .
.
3) Functia de productie este monoton crescatoare in raport cu fiecare din factorii de productie
Aceasta proprietate inseamna ca orice variatie pozitiva Dxi a factorului de productie oarecare xi conduce la un volum de productie mai mare, adica
![]()
|
In cazul in care functia de productie Q este derivabila partial, aceasta cerinta se exprima prin inegalitatea urmatoare:
![]() .
.
Aceste ultime inegalitati inseamna din punct de vedere economic ca productivitatile marginale in raport cu fiecare din factorii de productie sunt negative.
4) Productia are randament descrescator (legea randamentelor descrescatoare)
Section 1.01 Matematic aceasta proprietate se exprima prin cerinta:
![]() ,
,
ceea ce din punct de vedere economic inseamna ca o crestere permanenta a unui factor de productie conduce la un spor de productie din ce in ce mai mic.
5) Functia de productie este supraaditiva
Section 1.02
Daca 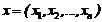 ,
,  sunt doi vectori de
productie oarecare, aceasta proprietare inseamna verificarea
cerintei
sunt doi vectori de
productie oarecare, aceasta proprietare inseamna verificarea
cerintei
![]()
ceea ce din punct de vedere economic inseamna ca efectul sumei a doi factori de productie este totdeauna cel putin egal cu suma efectelor factorilor de productie.
6) Functia de productie este omogena
Aceasta proprietate inseamna
ca daca ![]() este un vector de
productie oarecare, atunci exista un numar natural k (numit grad de omogenitate) asa
incat pentru orice
este un vector de
productie oarecare, atunci exista un numar natural k (numit grad de omogenitate) asa
incat pentru orice ![]() avem indeplinita
egalitatea urmatoare:
avem indeplinita
egalitatea urmatoare:
![]()
Din punct de
vedere economic aceasta proprietate inseamna ca daca
fiecare factor de productie se multiplica de ![]() ori, atunci volumul
productiei se multiplica de
ori, atunci volumul
productiei se multiplica de ![]() ori.
ori.
Observatia 1. Vom prezenta in continuare principalii
indicatori economici ai productiei, pentru comoditate vom considera
ca functia de productie depinde doar de doua variabile,
deci ![]() unde K reprezinta capitalul, iar L reprezinta forta de
munca.
unde K reprezinta capitalul, iar L reprezinta forta de
munca.
Exista urmatoarele categorii de astfel de indicatori:
1) indicatori medii:
a)
productivitatea medie a capitalului se noteaza cu Wk, este data de egalitatea ![]() si
masoara numarul mediu de produse realizate la o unitate de
capital;
si
masoara numarul mediu de produse realizate la o unitate de
capital;
b)
productivitatea medie in raport cu munca se noteaza cu WL, se calculeaza in
baza egalitatii ![]() si
masoara numarul mediu de produse obtinute cu o unitate de
forta de munca;
si
masoara numarul mediu de produse obtinute cu o unitate de
forta de munca;
c)
coeficient de inzestrare tehnica a muncii (inzestrarea muncii) se
noteaza cu k si se
calculeaza in baza egalitatii ![]() .
.
2) indicatori marginali:
Exista trei categorii de astfel de indicatori:
a)
productivitatea marginala a muncii se noteaza cu ![]() si se
calculeaza in baza relatiei
si se
calculeaza in baza relatiei ![]() ;
;
b)
productivitatea marginala a capitalului se noteaza cu ![]() si se
calculeaza cu ajutorul relatiei
si se
calculeaza cu ajutorul relatiei ![]() ;
;
c) rata marginala de substituire a factorilor:
.
rata marginala de substituirea capitalului prin munca se noteaza
cu ![]() si arata cu
cate unitati de capital trebuie inlocuita o unitate de
munca astfel incat productia sa ramana aceeasi.
Se calculeaza in baza egalitatii
si arata cu
cate unitati de capital trebuie inlocuita o unitate de
munca astfel incat productia sa ramana aceeasi.
Se calculeaza in baza egalitatii 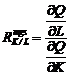 .
.
. rata marginala de substitutie a fortei de
munca prin capital se noteaza cu ![]() si
masoara cu cat trebuie sa creasca numarul de
unitati de forta de munca pentru a inlocui o unitate
de capital astfel incat productia sa ramana constanta.
Se calculeaza in baza egalitatii
si
masoara cu cat trebuie sa creasca numarul de
unitati de forta de munca pentru a inlocui o unitate
de capital astfel incat productia sa ramana constanta.
Se calculeaza in baza egalitatii  .
.
3) indicatori ai elasticitatii
a)
elasticitatea productiei in raport cu capitalul se noteaza ![]() , masoara cu cate procente creste
productia cand capitalul creste cu un procent si se
calculeaza in baza egalitatii
, masoara cu cate procente creste
productia cand capitalul creste cu un procent si se
calculeaza in baza egalitatii 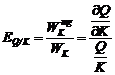 ;
;
b)
elasticitatea productiei in raport cu munca se noteaza ![]() , masoara numarul de procente cu care
creste productia atunci cand forta de munca creste cu
un procent si se calculeaza in baza egalitatii
urmatoare
, masoara numarul de procente cu care
creste productia atunci cand forta de munca creste cu
un procent si se calculeaza in baza egalitatii
urmatoare  .
.
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||
|
|||
Analize pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








