
| Afaceri | Agricultura | Comunicare | Constructii | Contabilitate | Contracte |
| Economie | Finante | Management | Marketing | Transporturi |
Finante
|
|
Qdidactic » bani & cariera » finante Modelul diagonal de selectie a portofoliului |
Modelul diagonal de selectie a portofoliului
MODELUL DIAGONAL DE SELECTIE A PORTOFOLIULUI
1. IPOTEZELE MODELULUI DIAGONAL
In elaborarea modelului sau, Sharpe porneste de la o intuitie fireasca pentru un cercetator atent: ansamblul covariatiilor in general pozitive, din cadrul riscului unui portofoliu poate avea un factor comun de determinare. Acest factor comun poate fi un indicator macroeconomic care influenteaza in mod substantial piata titlurilor financiare (indice bursier, rata de dobanda, PIB, etc.).
Pornind de la aceasta ipoteza, in cea mai mare parte realista (pe o piata financiara activa), putem afirma ca rentabilitatea fiecarui titlu financiar este in mare masura explicata (determinata) de evolutia factorului comun (a indicelui bursier RM, spre exemplu) ca variabila exogena: Ri=f(RM). Toti ceilalti factori care ar mai putea influenta rentabilitatea Ri sunt considerati endogeni si vor determina variatia neexplicata prin RM , respectiv riscul specific al titlului 'i'.
Ne propunem o mica paranteza prin care afirmam importanta capitala a modelului de piata (single index model or one factor model, in engleza). Identificarea acestui model si testarea validitatii corelatiei titlurilor 'i' cu factorul de piata 'M' au permis elaborarea modelului diagonal. La randul lui, modelul diagonal a inspirat constructia unui model celebru (CAPM) de evaluare a activelor financiare ca norma de remunerare de catre piata a investitiei in aceste active. In continuare, CAPM a inspirat un alt, nu mai putin celebru, model multifactorial (APT) de evaluare a activelor financiare. si lantul efectelor de propagare se continua in estimarea costului capitalului, in modelul multiperiodic, ca sa nu amintim decat pe cele mai actuale preocupari.
Putem afirma ca rentabilitatea unui titlu financiar depinde liniar de rentabilitatea de piata RM ecuatia dreptei de regresie putand fi scrisa sub urmatoarea forma
Ri=ai bi*RM+eI
in care, 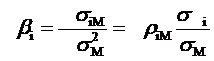
N
unde siM SProbs* Ris- E Ri Rjs-E RM
s=1
unde s = 1,2,3,,N stari posibile ale naturii in perioada de previziune.
Probs= probabilitate asociata fiecarei stari posibile ale naturii.
Aceasta corelatie are anumite proprietati, foarte utile in abordarile ulterioare:
![]()
![]()
![]()
![]()
Factorul rezidual ei ,rezultat prin aplicarea metodei de regresie a celor mai mici patrate, este deci expresia riscului specific (neexplicat prin factorul comun RM). Speranta sa matematica este nula (proprietate dobandita prin metoda celor mai mici patrate), iar dispersia sa se presupune a ramane constanta (aceeasi supozitie ca si constanta de legaturi dintre Ri si RM). Exprimand riscul specific al titluluui 'i' fara nici o legatura cu riscul celorlalte titluri sau cu riscul sistematic (de piata), este admisa cu temei teza independentei factorului ej fata de ceilalti factori ej si fata de cel al pietei (in consecinta, rij riM=0
Inca o ipoteza si trecem la virtutile modelului de piata care l-au facut atat de util in elaborarea modelelor viitoare. Se considera ca toate corelatiile siM (intre Ri, fiecare in parte, si RM ca factor comun) urmeaza o lege normala bivariabila: variatia RM determina, in marimi diferite (specifice fiecarui titlu), variatia sistematica a Ri; la randul ei, variatia Ri va induce o contributie specifica (particulara a titlului 'i') la variatia totala a RM. Ambele variatii ale Ri si RM urmeaza o lege normala (bivariabila, in cazul nostru). Daca toate covariatiile siM se inscriu in aceasta lege de distributie, atunci pentru definirea lor este suficienta cunoasterea urmatoarelor informatii: Ei, si2, EM, sM2, si riM (in total, 3n informatii despre titlurile i si 2 informatii despre factorul comun -indice bursier - , deci 32n+2 strict inferior lui 2n+n(n-1)/2 ).
Exemplu: Daca luam patru titluri (A, B, C, D) vom observa ca fara a introduce acest factor comun identificarea legaturilor dintre rentabilitatile lor se face apel la sase relatii (sAB sAC sAD sBC sBDsCD), iar in modelul Sharpe la numai patru (sAM sBM sCM sDM). Daca mai adaugam un titlu (E) vor fi necesare +4=10 realtii in fara a introduce foctorul comun fata de 4+1=5 relatii in modelul Sharpe .
Reprezentarea legaturilor intre rentabilitatile Ri si RM

2. EXPRIMAREA RISCULUI PORTOFOLIULUI IN MODELUL DIAGONAL
In aceste conditii de simplificare a intercorelatiilor dintre titluri, riscul total al fiecaruia se va defini in raport cu riscul de piata (sM2) si cu riscul specific (s2ei
![]()
![]()
In consecinta, riscul total al titlului i dobandeste, in modelul simplificat, o noua formulare:
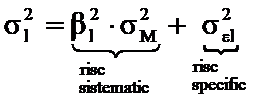
Suntem acum pregatiti sa abordam modelul diagonal de selectie a portofoliului. Deci, mai intai sa redefinim riscul portofoliului si apoi sa urmarim minimizarea lui. In forma sa simplificata, riscul total al portofoliului se va defini in functie de corelatiile titlurilor i cu M si nu cu perechile j
![]()
In care fiecare abatere se rescrie dupa modelul de piata:
![]()
![]()
Deci,
![]()
![]()
![]()
=0 =0 =0
In consecinta, pentru oricare i si j=1,2,..,n:
![]()
Cu aceste expresii noi ale riscului sl2 si ale covariatiilor sij , riscul total al portofoliului (sp2) se rescrie astfel:


|

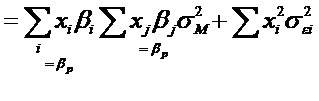
Expresia
riscului total al portofoliului in modelul diagonal evidentiaza cele doua
componente ale riscului: sistematic (![]() ) si specific
) si specific ![]()
![]()
Simplificarea este acum evidenta intrucat primul termen se obtine ca produs intre vectorii coloana xI si bi, pe de o parte; si variabila exogena sM2, iar al doilea termen se obtine ca produs intre vectorii linie si coloana xI si matricea diagonala sel3
Problema de rezolvat in modelul diagonal este urmatoarea:
![]()
stiind ca: ![]()
![]()
![]()
Recurgerea la functia Lagrange si cautarea minimului ei conduce la urmatorul sistem matriceal pentru determinarea frontierei eficiente:
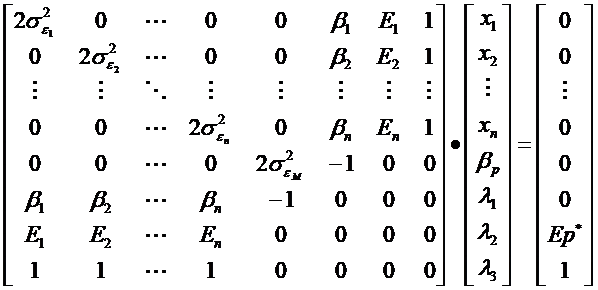
W X K
Compozitia portofoliilor eficiente cu risc minim, la o speranta de rentabilitate data (dorita = E*p), va fi solutia la sistemul matriceal: X=W-1*K.
3. APLICATIE A MODELULUI DIAGONAL
Scopul acestei aplicatii este identificarea procedurii operationale a modelului diagonal si nu economia de informatii necesare. Economia de informatii nu devine evidenta decat la portofolii formate din cel putin 5 titluri. La trei titluri avem nevoie chiar de mai multe informatii decat in modelul de baza .
In exemplu nostru estimarea vom estima un portofoliu de trei titluri (o actiune , o prima dubla , si o obligatiune) prin anticiparea pentru toata perioada viitoare a patru stari ale naturii:avant economic , crestere economica , stabilitate si recesiune.Astfel se dau rentabilitatile estimate ale celor trei titluri corespunzatoare fiecarei stari ale naturii si probabilitatile asociate fiecarei stari a naturii :
|
Stari ale naturii (s) |
Probas |
R1s |
R2s |
R3s |
|
Avant economic |
0,1 |
12 |
8 |
8 |
|
Crestere moderata |
0,4 |
8 |
2 |
2,5 |
|
Stabilitate |
0,4 |
4 |
2 |
5,5 |
|
Recesiune |
0,1 |
0 |
6 |
0 |
La aceste trei titluri initiale asociem valorile rentabilitatii (RM) si riscului (sM2) estimate pe ansamblul pietei financiare (indicele bursier) in aceleasi stari probabile ale naturii. Aceste valori centrale de referinta ne vor permite stabilirea corelatiei titlurilor initiale cu indicele pietei financiare si-n continuare selectia portofoliilor eficiente conform modelului diagonal.
Prin utilizarea modelului de piata vom determina intr-o prima faza parametrii sistemului de ecuatii de regresie liniara (ai si bi
|
Proba s |
RMs |
|
|
|
|
|
|
|
|
|
0,1 |
9,244 |
4,943 |
2,4433 |
6 |
2,9658 |
5 |
2,4715 |
4 |
1,9772 |
|
0,4 |
4,05 |
-0,0251 |
0,0252 |
2 |
-0,2008 |
-1 |
0,1004 |
-1,5 |
0,1506 |
|
0,4 |
3,96 |
-0,391 |
0,06115 |
-2 |
0,3128 |
-1 |
0,1564 |
1,5 |
-0,2346 |
|
0,1 |
1,926 |
-2,375 |
0,56406 |
-6 |
1,425 |
3 |
-0,7125 |
4 |
0,95 |
|
1 |
4,3 |
sM2=3,09 |
s1M=4,5028 |
s2M=2,0158 |
s3M=2,8432 |
||||
|
x |
x |
sM=1,76 |
b1=1,457 |
b2=0,65 |
b3=0,92 |
|
x |
x |
|
a1=-0,265 |
a2=0,205 |
a3=0,044 |
Incercand acum sa estimam rentabilitatile titlurilor
individuale (![]() ) in functie de rentabilitatea pietei pentru fiecare stare a
naturii (
) in functie de rentabilitatea pietei pentru fiecare stare a
naturii (![]() ) vom fi in masura sa determinam riscul specific al
titlurilor (sel2
) vom fi in masura sa determinam riscul specific al
titlurilor (sel2
|
Proba S |
RMs |
R1* |
se12 |
R2* |
se22 |
R3* |
se32 |
|
0,1 |
9,244 |
13,2035 |
0,14484 |
6,2136 |
0,319 |
8,5485 |
0,03 |
|
0,4 |
4,05 |
5,63585 |
2,23568 |
2,8375 |
0,2806 |
3,77 |
0,645 |
|
0,4 |
3,91 |
5,432 |
0,8202 |
2,7465 |
0,223 |
3,6412 |
1,382 |
|
0,1 |
1,926 |
2,5412 |
0,64577 |
1,4569 |
2,064 |
1,8159 |
0,33 |
|
1 |
4,3 |
6 |
3,8465 |
3 |
2,8866 |
4 |
2,387 |
Problema de minimizare a riscului portofoliului in modelul diagonal va avea urmatoarea forma concreta:
Min (x12*3,8465+x22*2,8866+x32*2,387)
+(x1*1,457+x2*0,65+x3*0,92)2*3,09 2
stiind ca:

Utilizarea functiei Lagrange si minimizarea ei conduce la urmatorul sistem matriceal al derivatelor partiale in functie de x1, x2, x3, bp l1 l2 l3

W X K
Matricea inversa W-1 are urmatoarele valori:
|
0,01356 |
0,02712 |
-0,04068 |
-0,00004 |
-0,00025 |
0,35082 |
-1,20884 |
|
0,02712 |
0,05424 |
-0,08135 |
-0,00008 |
-0,00005 |
-0,29836 |
1,58231 |
|
-0,04068 |
-0,08135 |
0,12203 |
0,00012 |
0,00075 |
-0,05245 |
0,62653 |
|
-0,00004 |
-0,00008 |
0,00012 |
0 |
-1 |
0,26895 |
-0,15637 |
|
-0,00025 |
-0,0005 |
0,00075 |
-1 |
-6,18 |
1,662096 |
-0,96639 |
|
0,35082 |
-0,29836 |
-0,05245 |
0,26895 |
1,662096 |
-1,92086 |
6,40472 |
|
-1,20884 |
1,5823 |
0,6265 |
-0,15637 |
-0,96639 |
6,40472 |
-0,27721 |
Cu ajutorul matricei inverse (W-1) putem obtine usor sistemul de ecuatii parametrice pentru determinarea frontierei eficciente si a riscului sistematic al acesteia:
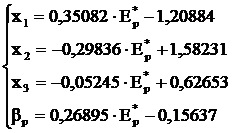
Pentru aceleasi valori dorite ale sperantei Ep* ca si-n exemplul anterior vom obtine urmatoarea compozitie a portofoliilor eficiente corespunzatoare (si care conduc in modelul diagonal la risc minim, a se vedea tabelul 11.3).
|
Ep* |
2,5 |
3 |
3,687 |
4 |
5 |
6 |
EM=4,3 |
|
X1 |
-33,2 |
-15,6 |
8,5 |
19,4 |
54,5 |
89,6 |
30 |
|
X2 |
83,65 |
68,7 |
48,2 |
38,9 |
9,1 |
-20,8 |
29,9 |
|
X3 |
49,55 |
46,9 |
43,3 |
41,7 |
36,4 |
31,2 |
40,1 |
|
|
0,516 |
0,65 |
0,835 |
0,92 |
1,188 |
1,457 |
1 |
|
|
3,03 |
1,98 |
1,146 |
9,997 |
1,483 |
3,445 |
0 |
|
|
|
3,29 |
3,3 |
3,6 |
5,84 |
10 |
3,09 |
Cu cat numarul titlurilor din portofoliu creste cu atat estimarile modelului diagonal se apropie de cele corecte.
O alta sursa a aproximarii o constituie reprezentativitatea
portofoliului de piata pentru titlurile analizate. Daca acest portofoliu nu
reprezinta un substitut perfect in care (![]() ), atunci estimarile in
modelul diagonal vor fi afectate corespunzator erorii de reprezentare a pietei
financiare.
), atunci estimarile in
modelul diagonal vor fi afectate corespunzator erorii de reprezentare a pietei
financiare.
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||
|
|||
Esee pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








