
| Afaceri | Agricultura | Comunicare | Constructii | Contabilitate | Contracte |
| Economie | Finante | Management | Marketing | Transporturi |
Economie
|
|
Qdidactic » bani & cariera » economie Modele econometrice cu ecuatii multiple |
Modele econometrice cu ecuatii multiple
MODELE ECONOMETRICE CU ECUATII MULTIPLE
I.1. Introducere
In modelele econometrice elementare se studiaza dependenta unei variabile endogene de o unica variabila exogena. Astfel de modele contin o singura ecuatie. Pentru studierea unor fenomene economice mai complexe este necesara introducerea in model a unor ecuatii suplimentare. Se obtin astfel modele cu mai multe ecutii, numite modele cu ecuatii multiple sau simultane. Procedurile de estimare vor fi in acest caz mai complicate, dar se bazeaza pe aceleasi principii generale ca si modelele cu o singura ecuatie, studiate in ciclul de licenta.
Cateva exemple:
a. Estimarea unei legi a cererii de bunuri.
In acest caz, modelul va contine trei ecuatii: una pentru cerere, una pentru oferta de bunuri si o ecuatie de echilibru cerere-oferta:

A estima
o lege a cererii inseamna ca, pornind de la observatiile ![]() , t = 1,2,,T sa determinam
parametrii necunoscuti din prima ecuatie. In functie de
dispunerea norului de puncte observate privind cererea de bunuri si
preturile acestora, intalnim urmatoarele situatii:
, t = 1,2,,T sa determinam
parametrii necunoscuti din prima ecuatie. In functie de
dispunerea norului de puncte observate privind cererea de bunuri si
preturile acestora, intalnim urmatoarele situatii:
Stabilitatea curbei cererii si ofertei cand t variaza.

Norul de puncte observate este in vecinatatea intersectiei celor doua curbe, care pot avea deplasari mici, independent una de alta. Nu putem asocia punctele observate uneia sau celeilalte curbe. In acest caz estimarea nu este posibila.
Stabilitatea curbei cererii.

Pentru numeroase produse agricole, de exemplu, cererea scade daca preturile cresc. Aceasta legatura intre pret si cerere depinde de comportamentul consumatorilor. Oferta, dimpotriva, se deplaseaza in sus sau in jos dupa cum a fost recolta. Punctele norului sunt acum dispuse de o parte sau alta a curbei cererii, care poate fi estimata.
Stabilitatea curbei ofertei.

Este posibil ca datorita cresterii veniturilor, de exemplu, curba cererii sa se deplaseze, iar cea a ofertei sa ramana stabila. Se obtine o reprezentare analoga celei dinainte si legea ofertei poate fi estimata in acest caz.
Curba cererii evolueaza in functie de venituri, curba ofertei evolueaza in functie de progresul tehnic si exista o deplasare simultana a celor doua curbe.

In acest caz nu putem estima nici cererea, nici oferta de bunuri. Ajustarea va conduce la curba care trece prin punctele de intersectie, care nu are nicio semnificatie.
Concluzie: Se pot obtine estimatii eronate daca se incearca estimarea parametrilor curbei cererii, fara a tine cont de curba ofertei de bunuri. Este necesar, deci, sa precizam ambele legi prin introducerea in model a unor variabile exogene noi, atat in legea cererii, cat si in legea ofertei.
b. Forma structurala si forma redusa
Forma structurala reproduce legile pietei asa cum sunt ele propuse de teoria economica. In aceasta forma, variabilele endogene si exogene intervin fara ca endogena sa se exprime unic in functie de exogena. Aceasta exclude, dupa cum s-a vazut, orice posibilitate de estimare sub aceasta forma (exista, totusi, o exceptie asupra careia vom reveni).
De exemplu, un sistem de doua ecuatii pentru cerere si oferta sub forma structurala este:

unde Vt este venitul consumatorilor, o variabila exogena care influenteaza cererea de bunuri, alaturi de pret pt, iar xt este o variabila exogena care influenteaza oferta de bunuri. In model, qt si pt sunt variabile endogene.
Forma redusa se obtine pornind de la forma structurala, exprimand fiecare variabila endogena in functie de exogenele modelului. In exemplul precedent, se obtine:

sau scris sub alta forma:
(*)
unde: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(*) este forma redusa a modelului. In aceasta forma nu mai este vorba nici de ecuatia cererii, nici de ecuatia ofertei. O regresie a lui pt si qt asupra Vt si xt este posibila, dar parametrii estimati a a b b nu mai au nicio semnificatie economica. Problema care se pune este, deci, de a determina parametrii formei structurale pornind de la estimatiile obtinute pe forma redusa. Aceasta este problema "identificarii" modelului econometric.
c. Functia consumului in modelul Keynes
Sub forma structurala, un model keynesian elementar este dat de sistemul de ecuatii:
(I) 
unde Ct este consumul menajului t si reprezinta o variabila endogena, Rt este venitul disponibil al menajului, considerat o variabila exogena. Prima relatie exprima consumul menajului ca o functie de venitul disponibil, iar a doua relatie arata ca menajul partajeaza venitul disponibil Rt intre consum Ct si economisire (investitii) It. Forma redusa asociata acestui model este:
(II) 
Inainte de a studia modelele cu ecuatii multiple, vrem sa comparam direct estimatorii obtinuti pe cele doua forme: structurala si redusa.
I.2. Estimarea pe forma structurala
O
regresie prin metoda celor mai mici
patate (MCMMP) pe ecuatia ![]() , conduce la estimatorul
, conduce la estimatorul ![]() :
:
 .
.
Utilizand
forma redusa pentru a calcula ![]() si
si ![]() , putem exprima
, putem exprima ![]() in functie de a. Procedam in felul urmator:
in functie de a. Procedam in felul urmator:
In forma redusa centram variabilele:


Inlocuim in expresia lui ![]() :
:

sau,
notand momentele empirice corespunzatoare cu ![]() ,
, ![]() si
si ![]() rezulta:
rezulta:
 .
.
Dar, pentru T (numar de observatii) suficient de mare:
 ,
, 
tind spre limite finite, in timp ce covarianta empirica:

tinde catre zero pentru ca I si e sunt independente. Atunci, pentru T suficient de mare, si tinand cont ca 0<a<1 (a este inclinatia marginala spre consum, consumatorul este prudent, nu aloca tot venitul pentru consum) se obtine:

insemnand
ca ![]() supraestimeaza pe
a.
supraestimeaza pe
a.
Concluzie
O regresie directa pe forma structurala introduce o deplasare sistematica a estimatorului parametrului a.
La fel
se poate arata ca ![]() obtinut pe forma
structurala subestimeaza pe b.
obtinut pe forma
structurala subestimeaza pe b.
I.3. Estimarea pe forma redusa si trecerea la forma structurala. Regresia indirecta
Notam
cu: ![]() ,
, ![]() ,
, ![]() si forma
redusa (II) se scrie:
si forma
redusa (II) se scrie:
 .
.
Aplicand
MCMMP celor doua ecuatii, se determina estimatorii ![]() si
si ![]() . Se stie (vezi cursul de econometrie din ciclul de
licenta) ca acesti estimatori sunt nedeplasati si
convergenti si se cunoaste distributia lor pentru T suficient de mare (chiar si
atunci cand
. Se stie (vezi cursul de econometrie din ciclul de
licenta) ca acesti estimatori sunt nedeplasati si
convergenti si se cunoaste distributia lor pentru T suficient de mare (chiar si
atunci cand ![]() nu urmeaza o lege
normala).
nu urmeaza o lege
normala).
Rezulta:
 ,
,  cu
cu ![]() si
si ![]() convergenti in
probabilitate catre a si b deoarece
convergenti in
probabilitate catre a si b deoarece ![]() si
si ![]() sunt ei
insisi convergenti. Se spune ca am obtinut
sunt ei
insisi convergenti. Se spune ca am obtinut ![]() si
si ![]() prin "regresie indirecta".
prin "regresie indirecta".
I.3.1. Distributia
limita a estimatorilor ![]() si
si ![]() obtinuti
prin regresie indirecta.
obtinuti
prin regresie indirecta.
Se
stie ca oricare ar fi distributia erorilor ![]() , deci si
, deci si ![]() , expresiile
, expresiile ![]() si
si ![]() au o distributie
limita normala, de medie egala cu zero.
au o distributie
limita normala, de medie egala cu zero. ![]() este un factor de
normalizare care evita, pentru T
suficient de mare, sa avem o distributie degenerata.
este un factor de
normalizare care evita, pentru T
suficient de mare, sa avem o distributie degenerata.
Putem scrie ca:

Pentru T suficient de mare ![]() si
si  .
.
Caracteristicile
distributiei ![]() se deduc, deci, din
cele ale lui
se deduc, deci, din
cele ale lui ![]() .
. ![]() are o distributie limita normala de medie zero
si ecart-tip dedus din cel al lui
are o distributie limita normala de medie zero
si ecart-tip dedus din cel al lui ![]() impartit la
impartit la ![]() . Se arata ca:
. Se arata ca:
 .
.
Concluzie: Corespondenta intre parametrii formei structurale si cei ai formei reduse este foarte rar, daca nu niciodata, asa de simpla ca in exemplul studiat.
Se impune deci, studierea cazului general al unui model cu ecuatii multiple.
I.4. Modele cu ecuatii multiple. Cazul general
Am vazut anterior necesitatea introducerii mai multor ecuatii in modelele econometrice. Cum tratam astfel de modele? Ce probleme apar in legatura cu formularea generala? Raspunsul la astfel de intrebari este dat in continuare.
I.4.1. Modelul general
Consideram n variabile endogene Y1, Y2,, Yn si m variabile exogene X1, X2,, Xm, pentru care se cunosc realizarile lor in decursul a T perioade. La momentul t, vom avea:
(1) 
sau, sub forma matriciala:
![]()
Unde:
 ,
,  ,
,  ,
,  ,
,  .
.
Nu se pot estima matricile B si C sub forma structurala (1), variabilele endogene figurand impreuna cu exogenele in fiecare ecuatie.
Daca vom presupune ca B este inversabila, atunci obtinem:
![]()
sau,
notand ![]() si
si ![]() , atunci:
, atunci:
(2) ![]() .
.
(2) este forma redusa a modelului general cu ecuatii multiple. Sub aceasta forma redusa vom putea estima matricea A, bineinteles cu unele ipoteze ce vor fi precizate. Dar, pentru a avea estimatori cu o semnificatie economica, trebuie sa revenim la matricile B si C.
|
I.4.2. Estimarea matricii A
Presupunem ca dorim sa aplicam MCMMP fiecarei ecuatii din modelul (2). Ipotezele modelului liniar general de regresie vor trebui sa fie indeplinite pentru fiecare ecuatie.
Prezentam
ipotezele referitoare la erorile ![]() (ele vor fi valabile
si pentru erorile
(ele vor fi valabile
si pentru erorile ![]() pentru ca
pentru ca ![]() . Aceste ipoteze sunt:
. Aceste ipoteze sunt:
- erorile in ecuatia i (i=1,,n) sunt independente:
![]() ,
, ![]()
- erorile relative la doua ecuatii i si j si doua momente t si t' sunt independente:
![]()
Altfel spus, presupunem independenta erorilor relative la observatii diferite.
- matricea
de varianta si covarianta a erorilor ![]() , este la momentul t:
, este la momentul t:

Ca si in cazul modelului
liniar general, presupunem ca matricea de varianta si
covarianta empirica a variabilelor exogene tinde catre o
matrice finita cand ![]() .
.
Daca
aceste conditii sunt indeplinite, se poate estima fiecare ecuatie din
modelul sub forma redusa. Estimatorii obtinuti sunt
nedeplasati si au varianta minimala. Obtinem astfel
matricea ![]() care are ca elemente
estimatori nedeplasati ai parametrilor formei reduse si care converg
in probabilitate catre valorile adevarate ale acestor parametri.
care are ca elemente
estimatori nedeplasati ai parametrilor formei reduse si care converg
in probabilitate catre valorile adevarate ale acestor parametri.
I.4.3. Intoarcerea la matricile B si C
Cunoscand
![]() , estimator al lui A,
vrem sa ne intoarcem la matricile B
si C. Dar A are n x m elemente, deci vom avea n x
m relatii intre coeficienti.
, estimator al lui A,
vrem sa ne intoarcem la matricile B
si C. Dar A are n x m elemente, deci vom avea n x
m relatii intre coeficienti.
Matricea B are n2 elemente, iar C are nm elemente. Se obtine un sistem de nxm ecuatii cu n2+nm necunoscute. Aceasta problema nu poate fi rezolvata, in general, decat daca intre parametrii formei structurale exista, apriori, n2 relatii sau restrictii.
Sa remarcam ca impartind succesiv membrul al doilea al fiecarei ecuatii din forma structurala prin b11, b22, ,bnn se obtine matricea B cu diagonala avand doar elemente egale cu 1, ceea ce reduce numarul de restrictii apriori la n2-n=n(n-1). Aceste restrictii pot fi de excludere (unele variabile absente in ecuatiile formei structurale, insemnind ca parametrii corespunzatori sunt nuli) sau de legaturi apriori intre elementele matricilor B si C.
I.4.4. Identificarea
Precizam cateva definitii relative la model in general si la fiecare ecuatie in particular.
a. un model se spune ca este identificat daca se pot estima toti coeficientii din matricile B si C cu ajutorul coeficientilor matricii A.
b. Un model este supra-identificat atunci cand exista restrictii asupra matricii A.
c. O ecuatie a modelului este identificata atunci cand se pot estima toti coeficientii din acea ecuatie.
d. O ecuatie a modelului este supra-identificata cand singurele restrictii care o afecteaza sunt suficiente pentru ca modelul sa fie supra-identificat.
e. O ecuatie supra-identificata este si identificabila in "aproape toate" structurile modelului.
f. Un model supra-identificat poate contine una sau mai multe ecuatii neidentificabile.
I.4.5. Criterii de identificare
Reluam modelul sub forma structurala, cu ipotezele anterioare (vom presupune, intre altele, absenta coliniaritatii variabilelor exogene in fiecare ecuatie). Precizam notiunea de restrictie relativa la o ecuatie din forma structurala.
a. Fiecare restrictie pe forma structurala se traduce printr-o relatie liniara omogena intre coeficientii unei ecuatii.
b. Definim o matrice a restrictiilor Ri relativa la ecuatia a i-a si o matrice de structura S obtinuta prin juxtapunerea matricilor B si C:
S=(BC)
Matricea Ri va fi construita astfel:
- daca Si este a i-a linie a matricii S si Rih este a h-a coloana a matricii Ri (corespunzatoare la a h-a restrictie din ecuatia i), atunci:
SiRih=0.
De exemplu, daca
restrictia consta in excluderea celei de a k-a variabile din ecuatia i
(adica egalitatea cu zero a coeficientului sik), atunci: ![]() , cu
, cu ![]() = 0 daca
= 0 daca ![]() ,
, ![]() = 1 ceea ce inseamna relatia:
= 1 ceea ce inseamna relatia: ![]() .
.
Constructia matricii Ri va fi exemplificata imediat.
Notam cu:
-n1 numarul de ecuatii veritabile din modelul cu ecuatii multiple;
-n2 numarul de identitati din model;
-n = n1 + n2 numarul de variabile endogene;
si enuntam urmatoarele criterii de identificare:
Fie
un model cu ecuatii multiple care satisface ipotezele precedente. A i-a ecuatie este identificata
daca si numai daca rangul matricii ![]() este egal cu n1+n2-1. Aceasta
este o conditie necesara si suficienta pentru identificare
si se numeste "conditia
de rang".
este egal cu n1+n2-1. Aceasta
este o conditie necesara si suficienta pentru identificare
si se numeste "conditia
de rang".
Pentru ca o ecuatie a modelului in forma structurala sa fie identificata trebuie ca numarul restrictiilor apriori la care sunt supusi coeficientii ecuatiei sa fie cel putin n1+n2-1. Aceasta conditie este necesara, dar nu si suficienta, si se numeste "conditia de ordin".
Fie
![]() numarul de
restrictii apriori care afecteaza ecuatia i.
numarul de
restrictii apriori care afecteaza ecuatia i.
a. Daca
![]() , atunci ecuatia a i-a
nu este identificata (se spune si ca este sub-identificata);
, atunci ecuatia a i-a
nu este identificata (se spune si ca este sub-identificata);
b. Daca
![]() atunci
ecuatia i este supra-identificata. Ea este, totodata
identificabila in "aproape toate" structurile modelului.
atunci
ecuatia i este supra-identificata. Ea este, totodata
identificabila in "aproape toate" structurile modelului.
c. Daca
![]() , atunci a i-a ecuatie nu este supra-identificata.
Ea poate fi identificabila in "aproape toate" structurile.
, atunci a i-a ecuatie nu este supra-identificata.
Ea poate fi identificabila in "aproape toate" structurile.
Observatie
Rezulta din definitiile date ca un model este supraidentificat daca exista mai mult de n1+n2-1 restrictii asupra oricarei ecuatii din forma structurala.
Exemple
I. Fie un model cu 3 variabile endogene Y1, Y2, Y3 si doua exogene X1, si X2. La momentul t, avem forma structurala:

Pentru a identifica usor matricile B si C scriem modelul inlocuind variabilele absente cu zero si respectand forma structurala generala (ordinea variabilelor este Y1, Y2, Y3, X1, si X2):
 ,
,
astfel ca matricile coeficientilor sunt:
 ,
,  ,
,
iar matricea de structura S este:
 .
.
Scriem acum matricile R1, R2, R3 ale restrictiilor asociate celor trei ecuatii din model.
Matricea R1 este:
 .
.
Matricile
Ri, i=1,2,3 au atatea coloane cate restrictii asupra
coeficientilor sunt in ecuatia respectiva (![]() ) si atatea linii cate variabile endogene si
exogene sunt in model (in ordinea Y1,
Y2, Y3, X1,
si X2), adica (n+m). Prima coloana din matricea R1 are elementele egale cu 0,
in afara de al doilea element, egal cu 1, care corespunde excluderii
variabilei Y2 din
ecuatia (1) (prima restrictie). A doua coloana are toate
elementele 0, in afara de al treilea, egal cu 1, corespunzand excluderii
variabilei Y3 din
ecuatia (1) (a doua restrictie). La fel, coloana a treia este 0, in
afara elementului al patrulea, egal cu 1, corespunzand excluderii variabilei X1 din ecuatie (a treia
restrictie).
) si atatea linii cate variabile endogene si
exogene sunt in model (in ordinea Y1,
Y2, Y3, X1,
si X2), adica (n+m). Prima coloana din matricea R1 are elementele egale cu 0,
in afara de al doilea element, egal cu 1, care corespunde excluderii
variabilei Y2 din
ecuatia (1) (prima restrictie). A doua coloana are toate
elementele 0, in afara de al treilea, egal cu 1, corespunzand excluderii
variabilei Y3 din
ecuatia (1) (a doua restrictie). La fel, coloana a treia este 0, in
afara elementului al patrulea, egal cu 1, corespunzand excluderii variabilei X1 din ecuatie (a treia
restrictie).
In mod similar se obtin matricile R2 si R3 corespunzatoare restrictiilor asupra coeficientilor din ecuatiile a 2-a si a 3-a.
 ,
,  .
.
Calculam acum matricile R corespunzatoare:
- pentru prima ecuatie:

- pentru a doua ecuatie:

- pentru a treia ecuatie:

Concluzii:
Prima ecuatie: ![]() , n1+n2-1=2
(n2=0, nu avem
identitati in model). Deoarece
, n1+n2-1=2
(n2=0, nu avem
identitati in model). Deoarece ![]() , ecuatia este supra-identificata (si modelul,
de asemenea). Matricea R are rangul
egal cu 2, deci rangR=n1+n2-1.
Ecuatia este identificabila in toate structurile, adica oricare
ar fi valorile atribuite coeficientilor care figureaza in matricea de
structura S;
, ecuatia este supra-identificata (si modelul,
de asemenea). Matricea R are rangul
egal cu 2, deci rangR=n1+n2-1.
Ecuatia este identificabila in toate structurile, adica oricare
ar fi valorile atribuite coeficientilor care figureaza in matricea de
structura S;
A doua ecuatie ![]() , deci
, deci ![]() . Ecuatia a doua poate fi identificata, rangul
matricii R este 2, in afara cazului
cand c12=0. Ea este
identificabila in "aproape toate" structurile (cu exceptia structurii
pentru care c12=0).
. Ecuatia a doua poate fi identificata, rangul
matricii R este 2, in afara cazului
cand c12=0. Ea este
identificabila in "aproape toate" structurile (cu exceptia structurii
pentru care c12=0).
A treia ecuatie: ![]() , deci
, deci ![]() . Dar cum rangul matricii R
este egal cu 1, aceasta ecuatie nu este niciodata identificabila.
Tot modelul, in ansamblu, este neidentificabil, deci, unele elemente ale
matricilor B si C nu vor putea fi niciodata
estimate.
. Dar cum rangul matricii R
este egal cu 1, aceasta ecuatie nu este niciodata identificabila.
Tot modelul, in ansamblu, este neidentificabil, deci, unele elemente ale
matricilor B si C nu vor putea fi niciodata
estimate.
II. Fie urmatoarea forma structurala:
 ,
,
adica un model cu trei
ecuatii, dintre care doua veritabile si ultima, o identitate.
Rescriem modelul pentru a pune in evidenta matricile B si C, introducand o variabila auxiliara ![]() ca factor pentru
fiecare constanta.
ca factor pentru
fiecare constanta.
 .
.
Matricea de structura este:

Matricea restrictiilor referitoare la prima ecuatie este:
 .
.
Singurele restrictii relative la prima ecuatie sunt doua restrictii de excludere. Matricea restrictiilor aferente celei de a doua ecuatii veritabile este:
 .
.
In a doua ecuatie exista trei restrictii: doua de excludere a variabilelor Y1 si X1 si una referitoare la faptul ca variabilele Y3 si X2 au acelasi coeficient (d), cu semne contrare, deci suma celor doi coeficienti este nula. Din acest motiv, pe a doua coloana a matricii R2 apare 1 in dreptul variabilelor Y3 si X2.
Matricile produs SR1 si SR2 sunt:
 ,
,  .
.
- prima
ecuatie: ![]() ;
; ![]() ,
, ![]() , in afara cazului
, in afara cazului![]() . Ecuatia este identificabila in "aproape toate"
structurile;
. Ecuatia este identificabila in "aproape toate"
structurile;
- a doua
ecuatie: ![]() ;
; ![]() ,
, ![]() , in afara cazului a=1.
Aceasta ecuatie este supraidentificata. Ea este identificabila
in aproape toate structurile.
, in afara cazului a=1.
Aceasta ecuatie este supraidentificata. Ea este identificabila
in aproape toate structurile.
Sa remarcam faptul ca a treia relatie in model este o identitate. Ea a fost tratata in matricea de structura S ca o ecuatie. Variabilele absente au fost inlocuite cu 0 in matrice. Putem utiliza aceasta identitate pentru a ajunge la un model cu doua ecuatii si numai doua endogene. Concluziile ar fi fost aceleasi pentru prima ecuatie (ea ramane neschimbata daca eliminam pe y2t, de exemplu).
Adesea este preferabil sa pastram modelul initial, inclusiv identitatea, pentru ca altfel ajungem din nou la combinatii intre coeficientii formei structurale. Ori, in toate cazurile trebuie sa revenim la estimarea coeficientilor formei initiale pornind de la aceste combinatii.
III. UN MODEL ECONOMETRIC AL PIETEI LEGUMELOR
Pentru a studia piata legumelor, vom face ipoteza ca cererea de legume este formata din doua componente: consumul de legume in stare proaspata al menajelor si cererea de legume pentru industrializare (conservare). Consumatorii de legume, indiferent de destinatie, se intilnesc pe aceeasi piata.
Consumul de legume in stare proaspata al menajelor in perioada t, notat cu Cmt, depinde de pretul legumelor (pt) si de venitul disponibil (Vt). Cererea de legume pentru conservare in perioada t, notata cu Cct este functie de pretul legumelor (pt) si de cererea de conserve din perioada precedenta (Ct-1). Oferta de legume in perioada t, notata cu Ot, este functie de pretul legumelor din perioada anterioara (pt-1). Rezulta urmatorul model econometric in forma structurala al pietei legumelor:
Ecuatia ofertei de legume:
![]()
Ecuatia cererii de legume in stare proaspata:
![]()
Ecuatia cererii de legume pentru conservare:
![]()
Ecuatia de echilibru a pietei legumelor:
![]()
unde ai, i=1,2,,8 sunt parametri reali necunoscuti, ce urmeaza a fi estimati, iar ε, ξ, μ sunt variabilele reziduale corespunzatoare. Este convenabil sa reducem numarul ecuatiilor din model prin inlocuirea variabilei "oferta de legume" cu suma cererilor, conform ecuatiei de echilibru. Obtinem astfel modelul:

![]()
Pentru a studia posibilitatile de
identificare ale acestui model econometric al pietei legumelor, este de
preferat o scriere matriciala a modelului. In acest scop introducem o
variabila auxiliara, ![]() . Rezulta urmatoarea forma matriciala a
modelului:
. Rezulta urmatoarea forma matriciala a
modelului:

Utilizind notatiile:

modelul devine:![]() , a carui forma redusa este:
, a carui forma redusa este:

Forma redusa a modelului se poate scrie si astfel:

unde:
 ,
,![]()
![]() ,
, ,
,
![]() ,
, ![]() ,
,![]() ,
, ![]()
 ,
, ![]() ,
,![]() ,
, 
Conditiile de identificare a ecuatiilor formei structurale sunt:
a) conditia de ordin: in acest model avem n=3. Fie ni si mi numarul de variabile endogene, respectiv exogene, absente in ecuatia i. Atunci:
Prima ecuatie: n1=1, m1=2
si ![]()
A doua ecuatie: n2=1, m2=2
si ![]()
A treia ecuatie: n3=1, m3=2
si ![]()
b) conditia de rang: conditiile necesare de identificare fiind indeplinite, trebuie studiata conditia de rang. Aplicarea sa conduce la constatarea ca modelul este supraidentificat, pentru ca cele trei ecuatii ale formei structurale sunt supraidentificate.
Se pot estima cei 12 parametri ai formei reduse. Cu acestia va trebui sa deducem in mod univoc pe cei opt parametri ai formei structurale pentru ca modelul sa fie bine identificat. Dar, relatiile anterioare dintre coeficientii formei reduse si cei ai formei structurale, fac acest lucru imposibil. Cei 12 parametri nu sunt independenti, intre ei exista unele relatii ca:
![]() ,
, ![]() ,
, ![]() , etc.
, etc.
Cei 12 parametri nu pot fi estimati, cu ajutorul metodei celor mai mici patrate, ecuatie cu ecuatie. Este nevoie sa se aplice metoda celor mai mici patrate in doua stadii pentru a estima coeficientii ecuatiilor supraidentificate, lucrind direct pe forma structurala a modelului. Informatiile asupra "sistemului" si a mediului sau sunt supra-abundente. Forma redusa obtinuta corespunde la mai multe forme structurale. Cea retinuta aici nu este decit o formulare particulara a functionarii "sistemului". Alte formulari ar putea conduce la aceeasi forma redusa.
Metodele de estimare utilizate in mod uzual nu se mai aplica la fel pe ecuatiile supraidentificate ale unui model cu ecuatii multiple. Existenta restrictiilor asupra matricii A a formei reduse nu permite determinarea prin MCMMP a unei solutii unice pentru estimatorii coeficientilor. Prin urmare, daca ecuatiile sunt simplu identificabile intoarcerea la coeficientii formei structurale pornind de la estimatiile obtinute pe forma redusa necesita adesea calcule laborioase. Vom vedea in continuare cum estimam astfel de modele.
I.5. Metode de estimare in modele cu ecuatii multiple
Criteriile de identificare aplicate fiecarei ecuatii dintr-un model econometric cu ecuatii multiple permit sa apreciem, inainte de a trece la estimarea modelului, daca toti coeficientii care apar in fiecare ecuatie pot fi determinati.
Vrem sa vedem ce metode de estimare pot fi aplicate in cazul modelelor ce ecuatii multiple.
Se disting patru cazuri:
Modelul este sub-identificat. Nu exista metode de estimare in acest caz. Trebuie construit un nou model care sa fie mai bine specificat.
Modelul este identificabil. In acest caz se poate aplica, printre altele, metoda regresiei indirecte (regresia pe forma redusa a modelului), revenind apoi la coeficientii formei structurale.
Modelul este supra-identificat. In acest caz nu se mai poate aplica regresia indirecta. Pentru aceasta situatie exista alte metode de estimare, ca: MCMMP in doua faze, MCMMP in trei faze, metoda verosimilitatii maxime cu informatie incompleta s.a. Evident, aceste metode pot fi aplicate si in cazul modelelor identificabile.
Pentru unele modele particulare, numite modele recursive, regresia directa pe o ecuatie a formei structurale este o metoda satisfacatoare.
I.5.1. Regresia indirecta
Fie modelul cu ecuatii multiple, in scriere matriciala, sub forma structurala:
![]() .
.
In cazul
in care matricea coeficientilor variabilelor endogene, B, este inversabila, atunci forma
redusa asociata modelului se scrie: ![]() ,
,
unde: ![]() si
si ![]() .
.
In cazul in care fiecare ecuatie din model este identificabila, se pot estima coeficientii matricei A din forma redusa (prin MCMMP) si in baza relatiilor de legatura intre coeficienti se determina estimatorii parametrilor formei structurale. Sub ipotezele precizate anterior estimatorii obtinuti sunt convergenti.
Singurul incovenient este ca determinarea coeficientilor matricilor B si C pornind de la coeficientii estimati in matricea A poate presupune uneori calcule laborioase chiar si pentru modele foarte simple.
Exemplu: Fie modelul cu ecuatii multiple (o varianta a modelului Keynes):

in care Ct si Yt sunt variabile exogene, iar Zt este o exogena. Modelul contine, deci, o singura ecuatie veritabila (n1=1) si o identitate (n2=1). Analizam daca modelul este identificabil aplicand criteriile de identificare din paragraful I.4.5. Matricile B si C din forma structurala generala conduc la matricea de structura:
![]() .
.
In
singura ecuatie veritabila (prima ecuatie) exista o
singura restrictie referitoare la coeficienti (restrictia
de excludere a variabilei exogene Zt).
Prin urmare, ![]() , iar matricea R1
este:
, iar matricea R1
este:
 , rezultand ca matricea
, rezultand ca matricea ![]() are rangul egal cu 1.
are rangul egal cu 1.
Deoarece
![]() , rezulta ca este indeplinita conditia de
rang, iar pentru ca
, rezulta ca este indeplinita conditia de
rang, iar pentru ca ![]() este indeplinita
si conditia de ordin. Modelul este, deci, identificabil si putem
aplica metoda regresiei indirecte.
este indeplinita
si conditia de ordin. Modelul este, deci, identificabil si putem
aplica metoda regresiei indirecte.
Scriem forma redusa a modelului:
 ,
,
unde: ![]() ,
, ![]() ,
, ![]() .
.
Sa presupunem ca dispunem de T=7 observatii anuale:
|
t |
Ct |
Zt |
Yt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Aplicarea MCMMP celei de a doua ecuatii din forma redusa conduce la estimatorii:
 ,
, ![]() .
.
Cu
datele din tabel, obtinem: ![]() ,
, ![]() ,
, ![]() ,
, ![]() si
si ![]() ,
, ![]() .
.
Determinam estimatorii parametrilor din forma structurala, cu ajutorul relatiilor dintre coeficienti:
![]() ,
, ![]()
![]() ,
, ![]() .
.
I.5.2. MCMMP in doua faze
Aceasta metoda se aplica atunci cand ecuatiile sunt supra-identificate. Desigur, daca ecuatia este identificabila, metoda conduce la aceleasi rezultate ca si regresia indirecta.
Reluam
modelul sub forma structurala ![]() si presupunem
ca prima ecuatie este supra-identificata. Aceasta prima
ecuatie poate fi scrisa sub forma:
si presupunem
ca prima ecuatie este supra-identificata. Aceasta prima
ecuatie poate fi scrisa sub forma:
(1) ![]() .
.
Este clar ca datorita restrictiilor care afecteaza aceasta ecuatie, unele variabile endogene si exogene pot lipsi din ecuatie.
Faza intai: Se estimeaza prin MCMMP ecuatiile din forma redusa corespunzatoare variabilelor endogene care figureaza in partea dreapta a ecuatiei (1). Aceste ecuatii se scriu astfel:
 .
.
Dupa efectuarea acestor regresii, obtinem:
(2) 
Faza a doua: Inlocuim variabilele endogene din ecuatia (1) cu expresiile lor date de (2). Obtinem:
(3) ![]() ,
,
unde ![]() ..
..
Aplicam
din nou MCMMP ecuatiei (3) si obtinem estimatorii ![]() ,
, ![]() ,nedeplasati si convergenti pentru
parametri b12, b13
,nedeplasati si convergenti pentru
parametri b12, b13
Pentru exemplificare, aplicam MCMMP in doua faze pe exemplul anterior si aratam ca se obtin aceleasi estimatii ca si prin metoda regresiei indirecte.
Faza
intai: Prima ecuatie a modelului, ![]() contine, in
partea dreapta, variabila endogena Yt. Vom aplica, in aceasta faza, MCMMP pe
ecuatia corespunzatoare lui Yt
din forma redusa, adica
contine, in
partea dreapta, variabila endogena Yt. Vom aplica, in aceasta faza, MCMMP pe
ecuatia corespunzatoare lui Yt
din forma redusa, adica ![]() si obtinem:
si obtinem:
 ,
, ![]() ,
, ![]() , sau
, sau ![]() .
.
Cu
datele din tabel, rezulta ![]() si
si ![]() si se pot calcula
valorile ajustate
si se pot calcula
valorile ajustate ![]() si erorile
si erorile ![]() .
.
Faza
a doua: Inlocuim Yt cu ![]() in ecuatia
in ecuatia ![]() , rezultand:
, rezultand: ![]() , unde
, unde ![]() si aplicam
MCMMP acestei ecuatii, rezultand estimatorii:
si aplicam
MCMMP acestei ecuatii, rezultand estimatorii:
(4)  ,
, ![]() . Dar, tinand cont ca
. Dar, tinand cont ca ![]() si
si ![]() rezulta ca
rezulta ca ![]() , care inlocuita in (4) conduce la:
, care inlocuita in (4) conduce la:
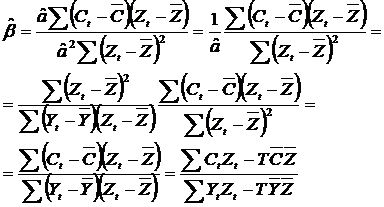
Cu
datele din tabel, avem ca ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() si:
si:
![]() ,
, ![]() , adica am obtinut acelasi rezultat ca si
prin regresie indirecta.
, adica am obtinut acelasi rezultat ca si
prin regresie indirecta.
MCMMP in doua faze evita calculele laborioase de intoarcere la coeficientii formei structurale, pornind de la estimarea formei reduse. Ea conduce la estimatori cu proprietati asimptotice destul de bune, dar pe esantioane mici nu ofera garantii prea mari asupra acestor proprietati.
I.5.3. MCMMP in trei faze
Metoda
celor mai mici patrate in trei faze porneste de la modelul econometric
in forma structurala ![]() a carui
forma redusa este
a carui
forma redusa este ![]() (unde
(unde ![]() si
si ![]() ) si parcurge urmatoarele faze:
) si parcurge urmatoarele faze:
Faza
intai: Se estimeaza prin MCMMP
obisnuita forma redusa, adica se regreseaza fiecare
variabila endogena din model pe toate variabilele exogene si se
obtin estimatiile preliminare ale endogenelor, notate ![]() .
.
Faza
a doua: Cu estimatiile endogenelor ![]() inlocuite in forma
structurala, fiecare ecuatie se poate scrie astfel:
inlocuite in forma
structurala, fiecare ecuatie se poate scrie astfel:
(1) 
Se aplica din nou MCMMP obisnuita acestor ecuatii rezultand estimatorii coeficientilor matricilor B si C. Pana aici s-a procedat exact ca in MCMMP in doua faze.
Faza
a treia: Folosind estimatorii parametrilor (![]() ) determinati in faza anterioara, prin inlocuire in
ecuatiile (1) se obtin noi estimatii ale endogenelor
) determinati in faza anterioara, prin inlocuire in
ecuatiile (1) se obtin noi estimatii ale endogenelor ![]() , care permit si estimarea erorilor
, care permit si estimarea erorilor ![]() , adica:
, adica:

Acest lucru permite obtinerea unei estimatii pentru matricea de varianta si covarianta a erorilor:

Se
aplica acum MCMMP generalizata pe ecuatiile (1). Prima
ecuatie din (1) se scrie sub forma matriciala (facand
sa varieze t de la 1 la T) astfel: ![]() , unde:
, unde:
 ,
,  ,
,  ,
,  .
.
Procedand la fel cu celelalte ecuatii din (1), se obtine sistemul:

care conduce la modelul general:
(2) ![]()
Unde:  ,
,  ,
,  ,
,  si
si  .
.
Aplicarea MCMMP generalizata modelului (2) conduce la estimatorul:
![]() .
.
![]() este estimatorul
obtinut prin MCMMP in trei faze.
este estimatorul
obtinut prin MCMMP in trei faze.
Proprietatile
estimatorilor obtinuti prin MCMMP in trei faze. Sa
remarcam mai intai ca daca erorile relative la doua
ecuatii ale formei structurale ![]() si
si ![]() nu sunt corelate,
acest lucru antreneaza independenta erorilor
nu sunt corelate,
acest lucru antreneaza independenta erorilor ![]() si
si ![]() . Matricea de varianta si covarianta
a erorilor
. Matricea de varianta si covarianta
a erorilor ![]() se reduce la o matrice
diagonala si estimatorii parametrilor obtinuti prin MCMMP
in trei faze coincid cu cei obtinuti prin MCMMP in doua faze.
se reduce la o matrice
diagonala si estimatorii parametrilor obtinuti prin MCMMP
in trei faze coincid cu cei obtinuti prin MCMMP in doua faze.
Proprietatile
estimatorilor ![]() obtinuti
prin MCMMP in trei faze depind de calitatea estimarii matricei de varianta
si covarinata a erorilor
obtinuti
prin MCMMP in trei faze depind de calitatea estimarii matricei de varianta
si covarinata a erorilor ![]() . In general ei poseda bune proprietati
asimptotice (nedeplasare si convergenta).
. In general ei poseda bune proprietati
asimptotice (nedeplasare si convergenta).
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |








