
| Biologie | Botanica | Chimie | Didactica | Fizica | Geografie |
| Gradinita | Literatura | Matematica |
Didactica
|
|
Qdidactic » didactica & scoala » didactica didactic clasa : a-xii a matematica - algebra, grupuri de matrice |
didactic clasa : a-xii a matematica - algebra, grupuri de matrice
Colegiul Tehnic "Transilvania" Baia Mare
PROIECT DIDACTIC
Clasa : a-XII-a A
Obiectul : Matematica - Algebra
Subiectul lectiei : GRUPURI DE MATRICE
Tipul lectiei : Lectie de formare de priceperi si deprinderi de calcul.
Conpetente generale :
1. Identificarea unor date si relatii matematice si corelarea lor in functie de contextul in care au fost definite.
2. Prelucrarea datelor de tip cantitativ, calitativ, structural sau contextual cuprinse in enunturi matematice.
3. Utilizarea algoritmilor si a conceptelor matematice pentru caracterizarea locala sau globala a unei situatii concrete.
4. Analiza si interpretarea caracteristicilor matematice ale unei situatii problema in scopul gasirii de strategii pentru optimizarea solutiilor.
5. Exprimarea caracteristicilor matematice cantitative sau calitative ale unei situatii concrete si a algoritmilor de prelucrare a acestora.
Competente specifice :
1. Recunoasterea structurilor algebrice, a multimilor de numere si de matrice.
2.1 Identificarea unei structuri algebrice, prin verificarea proprietatilor acesteia
2.2 Determinarea si verificarea proprietatilor unei structuri
Strategia didactica: activ-participativa.
1 Metode si procedee didactice: conversatia euristica , exercitiul, demonstratia, munca independenta.
2 Material didactic utilizat : manual clasa a-XII-a , fise de lucru .
3 Tipuri de actitati : frontala si individuala.
4 Procedee de evaluare: analiza raspunsurilor, observarea sistematica a atentiei, verificarea cantitativa si calitativa a temei.
Scenariu didactic:
1. Moment organizatoric: Verificarea prezentei elevilor si notarea absentelor (daca sunt) in catalog;
Asigurarea unei atmosfere adecvate pentru buna desfasurare a orei ;
2. Captarea atentiei: Verificarea temei elevilor prin sondaj folosind dialogul profesor-elev; elev-elev, prin confruntarea rezultatelor (in cazul in care apar diferente se rezolva exercitiile la tabla ).
3. Informarea elevilor asupra obiectivelor lectiei: Se anunta si se scrie pe tabla titlul lectiei: GRUPURI DE MATRICE
GRUPURI DE MATRICE
Fie n N* si Mn (R) multimea matricelor patratice de ordinul n cu elemente numere reale.
Dupa cum se stie, multimea Mn (R) impreuna cu adunarea matricelor formeaza un grup comutativ, iar cu inmultirea matricelor formeaza un monoid necomutativ.
In continuare se vor pune in evidenta cateva submultimi ale multimii Mn (R), care impreuna cu inmultirea matricelor formeaza grupuri.
~Grupul liniar general de grad n~
Fie A Mn (R). Se stie ca matricea A este inversabila in monoidul (Mn (R), ) daca si numai daca det (A) ≠ 0. Multimea unitatilor monoidului (Mn (R), ) se noteaza GLn (R) si avem :
GLn (R) =.
TEOREMA
Perechea ( GLn (R) , ) este grup necomutativ, numit grup liniar general de grad n peste R.
▪ Demonstratie
Fie A, B GLn(R). Rezulta ca det(A·B)=det(A) · det(B) R* , deci AB GLn (R). Asadar, multimea GLn (R) este parte stabila a multimii Mn (R) in raport cu inmultirea matricelor.
Inmultirea matricelor este asociativa si admite elementul neutru In Mn (R). Deoarece det(In) =1 R* , rezulta ca In GLn(R).
In consecinta, inmultirea matricelor pe multimea GLn (R) admite element neutru si anume matricea In.
Daca A GLn(R),
atunci det(A-1) = ![]() R*
si
se obtine ca A-1 GLn(R).
R*
si
se obtine ca A-1 GLn(R).
In concluzie, (GLn(R), .) este grup.
~Grupul matricelor ortogonale~
Fie A Mn (R).
. Definitie Matricea A
Mn (R) se numeste matrice ortogonala daca ![]() = In.
Multimea
matricelor ortogonale de ordinul n se noteaza On (R).
= In.
Multimea
matricelor ortogonale de ordinul n se noteaza On (R).
˝Observatii˝
1.Daca A On (R), atunci det (A)=.
Intr-adevar, din A On
(R) se obtine ca ![]() =In.
(1)
=In.
(1)
Din relatia (1) se obtine succesiv:
1 = det(In)
= det(![]() det(
det(![]() ) · det(A) = (det (A))².
) · det(A) = (det (A))².
|
Asadar, det (A)
2.Exista incluziunea On (R)
![]() GLn (R).
GLn (R).
TEOREMA
Perechea (On(R), ) este un grup necomutativ, numit grupul matricelor ortogonale de ordinul n.
▪ Demonstratie
Fie A, B On (R);
rezulta ca ![]() = In si
= In si ![]() = In.
= In.
Avem: ![]() · (AB)= (
· (AB)= (![]()
![]() ) · (AB)=
) · (AB)= ![]()
![]() ) · B=
) · B=![]() = In.
= In.
Asadar, AB On (R), iar multimea On (R) este parte stabila a multimii Mn (R) in raport cu inmultirea matricelor.
Sa verificam axiomele grupului.
G1) Axioma asociativitatii. Inmultirea matricelor pe multimea On (R) este asociativa, fiind operatie indusa de inmultirea matricelor pe Mn (R) ( proprietate de ereditate a asociativitatii).
G2) Axioma
elementului neutru. Deoarece ![]() In =
In se obtine ca
In =
In se obtine ca ![]() In ·
In = In, deci In On (R). Rezulta ca In este elementul neutru
al inmultirii
matricelor pe multimea On (R).
In ·
In = In, deci In On (R). Rezulta ca In este elementul neutru
al inmultirii
matricelor pe multimea On (R).
(G3) Axioma elementelor simetrizabile.
Fie A On (R).
Din observatia 1 rezulta ca
det(A) = ± 1, deci matricea A este inversabila in monoidul Mn (R). Din relatia ![]() = In se deduce ca A-1
= In se deduce ca A-1 ![]() . Folosind aceasta relatie se
obtine
. Folosind aceasta relatie se
obtine ![]() (A-1) · A-1
=
(A-1) · A-1
=![]()
![]() ) · A-1 = A
· A-1 = In,
deci A-1 On
(R), iar elementul simetric al matricei A in On (R)
este matricea A-1.
) · A-1 = A
· A-1 = In,
deci A-1 On
(R), iar elementul simetric al matricei A in On (R)
este matricea A-1.
Inmultirea matricelor nu este comutativa. In concluzie (On (R), .) este grup necomutativ.
~Exercitii~
1. Se considera matricea 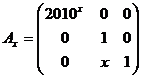 , pentru xR
si
multimea
, pentru xR
si
multimea ![]()
a)
Sa se verifice ca ![]() , unde
, unde 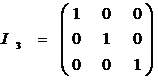
b) Sa se demonstreze
ca ![]()
c) Sa se arate
ca ![]() este grup comutativ.
este grup comutativ.
Rezolvare:
a)
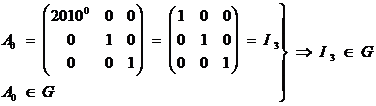
b)
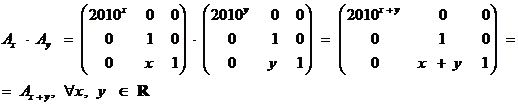
c) Conform punctului b) ![]() G este parte stabila a lui
G este parte stabila a lui ![]() in raport cu "".
in raport cu "".
G1) Asociativitatea . Inmultirea matricelor
pe multimea G este asociativa deoarece este operatie indusa
de inmultirea matricelor pe ![]()
G2)
Comutativitatea: ![]()
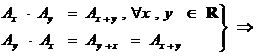 " comutativa.
" comutativa.
G3) Elementul neutru:
![]() astfel incat
astfel incat ![]()
![]() element neutru.
element neutru.
G4) Elementele simetrizabile:
![]() astfel incat
astfel incat ![]()
![]()
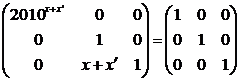
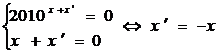
![]() este simetricul lui
este simetricul lui ![]()
2. Fie  . Sa se arate
ca
. Sa se arate
ca ![]() este grup comutativ.
este grup comutativ.
Rezolvare:
Fie  . Calculam puterile matricei A, pentru a determina
multimea M.
. Calculam puterile matricei A, pentru a determina
multimea M.


![]()

![]()
Inmultirea matricelor pe
multimea M este asociativa deoarece este operatie indusa de
inmultirea matricelor pe ![]()
Alcatuim tabla operatiei de inmultire pe M:
|
|
I3 |
A |
A2 |
|
I3 |
I3 |
A |
A2 |
|
A |
A |
A2 |
I3 |
|
A2 |
A2 |
I3 |
A |
Din care deducem ca "" pe M este comutativa, admite elementul neuru I3 si orice element din M este simetrizabil.
In concluzie ![]() este grup comutativ.
este grup comutativ.
3. Fie  . Sa se arate ca
G este grup comutativ in raport cu inmultirea matricelor.
. Sa se arate ca
G este grup comutativ in raport cu inmultirea matricelor.
Rezolvare:

G este parte stabila a lui ![]() in raport cu inmultirea matricelor
in raport cu inmultirea matricelor ![]()
Fie ![]() si
si ![]()
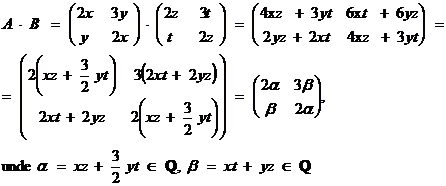
![]()

G1) Asociativitatea .

Inmultirea matricelor pe G este asociativa .
G2) Comutativitatea: "" comutativa ![]()
Fie ![]() si
si ![]()
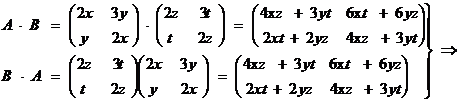
![]()
G3). Elementul neutru
Verificam daca ![]()
![]() si
si ![]()
![]()

![]() astfel incat
astfel incat ![]()
G4). Elementele simetrizabile:
![]() astfel incat
astfel incat ![]()
Fie ![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
4. Fie G=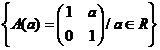 M2 (R)
M2 (R)
Sa se arate ca (G,) este grup abelian
Rezolvare:
G parte stabila a
lui M2 (R) in raport cu "·" ![]()
![]() A(a),A(b) G
A(a),A(b) G ![]() A(a)·A(b) G]
A(a)·A(b) G]
A(a) ·A(b) = ![]()
![]()
![]()
![]() , unde
, unde ![]() = a+b R
= a+b R ![]() G parte stabila.
G parte stabila.
"·" pe G este asociativa fiind operatie indusa de inmultirea matricelor pe M2(R)
"·" comutativa ![]()
![]() A(a), A(b) G, A(a) · A(b)
= A(b) · A(a)
A(a), A(b) G, A(a) · A(b)
= A(b) · A(a)
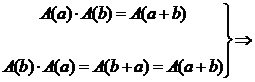 "·"
comutativa
"·"
comutativa
``Elementul neutru ``: A(0) = ![]() = I2
= I2
![]() A(0) G astfel incat A(a) · A(0) = A(0) · A(a) = A(a) ;
A(0) G astfel incat A(a) · A(0) = A(0) · A(a) = A(a) ; ![]() A(a) G
A(a) G
``Elementele simetrizabile``:
![]() A(0) G;
A(0) G; ![]()
![]() Є G astfel incat
A(a) ·
Є G astfel incat
A(a) · ![]()
![]() · A(a) = I2
· A(a) = I2 ![]() A(a+
A(a+![]() ) = A(
) = A(![]() +a) = A(0)
+a) = A(0) ![]()
![]()
![]()
![]() = -a R
= -a R
![]() [A(a)]ˉ¹ =
A(-a) G .
[A(a)]ˉ¹ =
A(-a) G .
5. Consolidarea cunostintelor si asigurarea feed-back-ului : Fiecare elev va primi cate o fisa de lucru . Pe parcursul rezolvarii exercitiilor, profesorul intervine cu intrebari, adresate atat elevilor de la tabla cat si celor din clasa, pentru a se clarifica demersul rezolvarii.
6. Tema pentru acasa Se vor propune spre rezolvare ca tema pentru acasa , exercitiile ramase nerezolvate din fisa .
7. Aprecieri: se noteaza elevii care s-au evidentiat in timpul orei.
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||
|
|||
Documente online pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








