
| Biologie | Botanica | Chimie | Didactica | Fizica | Geografie |
| Gradinita | Literatura | Matematica |
Didactica
|
|
Qdidactic » didactica & scoala » didactica didactic Clasa: a IX-a, matematica, graficul functiei de gradul I |
didactic Clasa: a IX-a, matematica, graficul functiei de gradul I
Proiect didactic
Clasa: a IX-a
Unitatea de invatamant: Colegiul Tehnic Energetic
Obiect: Matematica
Unitatea de invatare: Functii si ecuatii
Tema lectiei: Graficul functiei de gradul I
Tipul lectiei: Dobandire de cunostinte
Scop: reprezentarea grafica a functiei de gradul I
Competente specifice:
1. Recunoasterea unor corespondente care sunt siruri, progresii, functii
2. Calculul valorilor unor functii care modeleaza situatii practice in scopul caracterizarii acestora
2. Reprezentarea in diverse moduri a unor corespondente functii, siruri in scopul caracterzarii acestora
Obiective operationale
sa reprezinte imaginea deometrica a graficului functiei f:R->R , f(x)=ax+b
sa stabileasca monotonia unei functii
Obiective TIC
sa deschida aplicatia Excel
sa introduca date si formule
sarealizeze grafice
Metode si procedee: conversia euristica, explicatia, demonstrarea, exercitiul, munca independenta
Mijloace de invaramant: manual, fise de munca independenta, calculatorul, soft Microsoft Excel
Forme de organizare: frontal, individual
Desfasurarea activitatii
|
MOMENTELE LECTIEI |
OBIECTIVE OPERATIONALE |
DESFASURAREA ACTIVITATII |
METODE SI PROCEDEE |
FORME DE ORGANIZARE |
EVALUARE |
||||
|
1. Moment organizatoric |
|
Se asigura cadrul optim necesar desfasurarii orei |
|
|
|
||||
|
2. Captarea atentiei |
|
|
|
|
|
||||
|
3. Reactualizarea cunostintelor |
|
Profesorul pune intrebari
|
conversatia |
frontal |
|
||||
|
4. Anuntarea scopului si a obiectivelor |
|
- definirea functiei - valoarea unei functii intr-un punct |
|
|
|
||||
|
5. Prezentarea noului continut |
|
|
|
|
|
||||
|
6. Dirijarea invatarii |
|
Exercitii propuse pe calculator |
Exercitiul |
Frontal |
Orala |
||||
|
7. Obtinerea performantei |
|
Elevii realizeaza exercitii din fisa de munca independenta |
Munca independenta |
Individual |
Scrisa |
||||
|
8. Asigurarea transerului cunostintelor |
|
Elevii isi noteaza tema. Se fac aprecieri cu privire la participarea elevilor la lectie |
|
Frontal |
|
Graficul functiei de gradul I
graficul functiei de gradul intai este o dreapta de ecuatie y=ax+b
pentru trasarea unei drepte sunt necesare 2 puncte care apartin graficului ( de cate puncte este deternimata o dreapta ? )
faptul ca M0(x0,y0) apartine graficului se traduce algebric prin egalitatea y0=ax0+b ( se spune: coordonatele punctului verifica ecuatia dreptei )
se aleg doua valori x1Kx2 pentru care se calculeaza f(x1), f(x2)
punctele M1(x1,f(x1)), M2(x2,f(x2)) determina in plan dreapta de ecuatie y=ax+b
in multe din situatii este usor sa luam cele doau puncte, intersectiile graficului cu axele de coordonate M1(0,f(0)=b), M2(-b/a,0)
se propune elevilor trasarea urmatoarelor grafice :
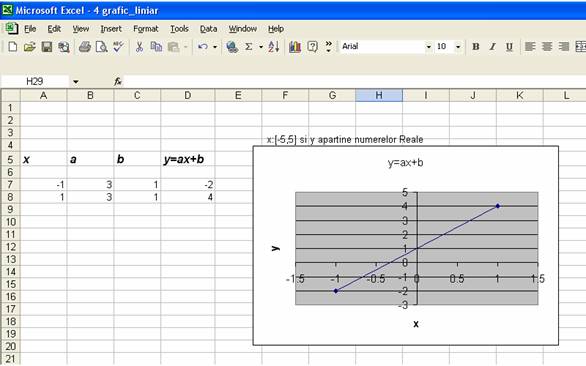
1. f1:R->R ,f1(x)=3x+1
2. f2:R->R ,f2(x)=-3x+1
se completeaza tabelul de valori pentru functia f
|
x |
|
-1 |
1 |
=> A(-1,-2)X Gf1 |
|
f1(x) |
|
-2 |
4 |
B(-2,4)X Gf1 |
|
x |
|
-1 |
1 |
=> A(-1,4)X Gf2 |
|
f2(x) |
|
4 |
-2 |
B(1,-2)X Gf2 |

Ce observati comparand cele 2 grafice reprezentate ?
in cazul graficului f1 acesta urca deci functia este sctrict crescatoare pe o multime
in cazul graficului functiei f2 aceasta coboara deci functia e strict descrescatoare
Concluzia este ca :
pt f:R->R , f(x)=a+b, cu a > 0 , f crescatoare
pt f:R->R , f(x)=ax+b, cu a<0 , f descrescatoare
se cere elevilor sa prezinte grafic alte functii si sa stabileasca monotonia acestora:
f:R->R , f(x)=2x+1 si f(x)=-2x+1
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||
|
|||
Referate pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








