
| Afaceri | Agricultura | Comunicare | Constructii | Contabilitate | Contracte |
| Economie | Finante | Management | Marketing | Transporturi |
Economie
|
|
Qdidactic » bani & cariera » economie Bazele studiului bunastarii: optimul de tip Pareto - conceptul de echitate |
Bazele studiului bunastarii: optimul de tip Pareto - conceptul de echitate
ECONOMIA BUNASTARII
Planul lectiei:
Specificul functiei bunastarii
Bazele studiului bunastarii: optimul de tip Pareto
Obiectivele modelului
Ipoteze si restrictii metodologice
Rationamentul nmodelului
Concluzii
Eficienta in combinarea factorilor
Eficienta in nivelul productiei
Eficienta in consum
Eficienta in productie si consum
Concluzii extinse
Modelul dinamic
Conceptul de echitate
Cateva repere teoretice
Echitate si eficienta in modelul Pareto
Inegalitatea economica
Cauze ale inegalitatii
Studiul inegalitatii
Politici de egalizarea veniturilor
De revazut, in prealabil:
Curentul marginalist (Lectia Introductiva)
Curbe izocuante si izocost, curba de expansiune (Lectia I)
Curbe de indiferenta si linii buget (Lectia II)
Avem de a face, in aceasta lectie, cu o functie calitativ diferita de cele studiate mai sus , cu rezerva ca cunostintele ei se fundamenteaza totusi pe cele deja studiate in cele de mkai sus.
Specificul functiei bunastarii
Trei puncte de vedere individualizeaza acesta noua functie:
(A) Variabilele independente (exogene) - dupa care, in aceeasi ordine ca in cazurile functiilor deja studiate, functia bunastrarii (Sw) apare drept:
Sw = f (Q; D; H; L; P; S; R; Z)
unde:
Q este cantitatea (oferta) totala de bunuri si servicii
D este distribitia sociala a lui Q;
H este gradul de sanatate publica;
L este timpul liber general (social);
P este gradul de poluare a mediului;
S este stabilitatea politica;
R sunt conditiile climatice, fertilitatea naturala a solului etc.
Z sunt, ca si pentru celelalte functii, alti factori de mai mica importanta.
(B) Indivizii sociali - este vorba aici, mai precis, de utilitati individuale (u1, 2, . , n):
Sw = f ( u1, 2, . , n)
considerandu-se si un numar finit de indivizi - intrucatva, functia bunastarii se refera la indivizi, colectivitati si comunitati asemanator functiei cererii.
(C) Static, versus dinamic, respectiv:
folosind formalizarile (A) si (B) de mai sus (static);
avand in vedere si schimbarea acestor date (dinamic), ceea ce:
(a) exemplifica starea economica de tranzitie;
(b) imbunatateste sau dimpotriva starea materiala a indivizilor sociali, ca referinta.
Bazele studiului bunastarii: optimul de tip Pareto
Vilfredo Pareto[2] este notat ca parinte al unor studii dezvoltate pana astazi pe o baza necontrazisa funcamental.
Obiectivele modelului
Regasim in dreptul functiei bunastarii si o alta distinctie - semnificand raportarea subiectiva la realitatea economica (obiectiva) sau realitatea asteptata (din nou subiectiva) de la economie. Functia bunastarii, emanand de la Vilfredo Pareto si marginalisti, isi pastreaza doua obiective (functii-obiectiv): (1) eficienta si (2) echitatea.
Eficienta -- in definitia tipic marginalista, respectiv "eficienta (de tip) Pareto" - este inteleasa drept acea stare economica care nu mai suporta imbunatatiri sau ameliorari. Cu alte cuvinte, oricare redistribuire materiala de la momentul eficientei Pareto nu poate avea decat efect negativ, respectiv acela de pierdere a starii de eficienta Pareto. Eficienta Pareto se va localiza pe trei niveluri, anume:
(a) nivelul combinarii factorilor;
(b) nivelul productiei propriuzise - rezultand bunuri si servicii;
(c) nivelul consumului - acelorasi bunuri si servicii.
Observatie: Cele trei niveluri ale eficientei Pareto pastreaza in comun, doua cate doua:
zona productiei - pentru nivelurile (a) si (b);
categoria bunurilor si serviciilor: (b) si (c).
La randul ei, echitatea - un concept studiat ceva mai tarziu, in literatura economica - va veni, totusi, sa se grefeze pe acelasi model Pareto si va cauta reconcilierea tehnica cu acesta.
Ipoteze si restrictii metodologice
Diagrama IV.1 listeaza ipotezele si restrictiile caracteristice modelului de baza Pareto - in partea urmatoare, concluziile modelului vor fi confruntate si cu inlaturarea (relaxarea) acestor restrictii.
Diagrama IV.1
Modelul eficientei Pareto:
ipoteze si restrictii metodologice
|
|
denumire |
explicatii |
|
|
economia reala |
fara moneda si implicatiile ei, incepand cu cele asupra nivelului preturilor. |
|
|
economia inchisa |
fara fluxuri materiale de intrare/iesire in/din sistem |
|
|
2 bunuri |
x & y (oarecare si substitute) |
|
|
2 factori de productie |
capital (k) & munca (L) |
|
|
2 indivizi sociali |
A & B |
|
|
oferta fixa de bunuri |
|
Rationamentul modelului
Graficele IV.1 figureaza separat productiile pe termen lung (izocuante-izocosturi eficiente si curbe de expansiune eficienta a productiei) ale celor doua bunuri, (x) si (y), presupuse de model.
 kx ky
kx ky
(x3) (y3)
(x2) (y2)
(x1) (y1)
Ox Lx Oy Ly
(a) (b)
Graficele IV.1
Explicatie grafica:
Date fiind cele doua grafice de forma binecunoscruta din Lectia I, urmeaza ca in Graficele IV.2, urmatoare, sa aiba loc mai intai rasturnarea Graficului IV.1 (b) peste Graficul IV.1 (a), cu re-localizarea celor doua perechi de axe rectangulare. Metoda se numeste "Edgeworth-Bowley (EB)", doua nume de autori care au continuat si clarifica demersul inceput de Vilfredo Pareto - Caseta Edgeworth-Bowley (EB) constituie fundamentul de studiu al Graficului IV.2.
 (Ly) LyA Oy
(Ly) LyA Oy
(kx)
kxA A kyA
(ky)
Ox LxA (Lx)
Graficul IV.2 (a)
Comentariu grafic:
Cele doua perechi de axe rectangulare rezulta ca in acest Grafic - de altfel, fundamental si cel mai important din tot demersul:
axele rezulta paralele doua cate doua: ale muncii (L) sunt orizontale; ale capitalului (k) sunt verticale;
rezultatul - sub forma Casetei -- mai este, insa, si "inchiderea" resurselor economiei in studiu, fireste in materiile celor doi factori de productie.
Sunt eludate, deocamdata, curbele izocuante si izocost pentru a clarifica conditia oricarui punct A:
acesta are, nu o singura pereche de coordonate, ci doua, corespunzatoare factorilor atribuiti celor doua productii;
insumarea coordonatelor-munca va totaliza resursele de munca totale ale economiei; idem, pentru coordonatele-capital si totalul resurselor de capital ale economiei:
LxA + LyA = L
KxA + kyA = k
iar acestea se intampla independent de localizarea punctului A in interiorul Casetei si defineste eficienta Pareto a combinarii factorilor de productie: utilizarea integrala a resurselor de factori la dispozitia economiei;
mai rezulta, geometric de astadata, ca oricare dreapta (curba sau functie rectilinie) trecand prin punctul A va forma, cu cele doua perechi de axe, unghiuri corespunzator egale.
 (kx) (Ly) LyA /A' Oy
(kx) (Ly) LyA /A' Oy
kxA' A' kyA'
kxA A kyA
(ky)
Ox LxA/A' (Lx)
Graficul IV.2 (b)
Comentariu grafic:
Exista una si aceeasi curba de expansiune a productiei eficiente, comuna celor doua productii --propozitia are valoare de teorema si rezulta din cele desprinse din Graficul (Caseta) IV.2 (a):
daca, spre exemplu, curba de expansiune proprie productiei (x) nu ar eveni in Oy, atunci unul dintre factorii de productie (k sau L) nu s-ar epuiza, ceea ce ar insemna ineficienta Pareto;
daca si oriunde, in parcursurile lor dintre cele doua origini (Ox si Oy), cele doua curbe de expansiune ar cunoaste itinerarii (pozitionari) diferite, atunci nu am mai avea de a face cu unicitatea punctului A, ca in cazul Graficului IV.2 (a), ci cu puncte A si A' diferite, pentru care resursele de capital (pe Grafic, dar posibil si munca) fie nu ar fi epuizate - ineficienta Pareto -, fie s-ar situa sub necesitatile celor doua productii asociate - contrazicand ipoteza economiei inchise.
 (kx) (Ly) LyA LyA' Oy
(kx) (Ly) LyA LyA' Oy
(y) (x)
kxA' A' kyA'
kxA A kyA
(ky)
Ox LxA LxA' (Lx)
Graficul IV.2 (c)
Comentariu grafic:
Comuniunea curbei de expansiune a celor doua productii eficiente reduce eficienta Pareto - presupusa initial (Graficul a) pe intreaga suprafata a Casetei - la aceasta curba-diagonala. Acum, punctele A si A' apartin acestei curbe si astfel sunt presupuse a fi simultan puncte de eficienta. Totusi, odata cu localizarea diferita a punctelor A si A' se mai observa si localizarea izocuantelor-perechi (x) si (y) semnificand:
folosirea a OxLxA' resurse de munca pentru productia (x), respectiv a LyAOy resurse de munca pentru productia (y);
similar pentru resursele de capital: OxkxA' pentru productia (x) si respectiv OykyA pentru productia (y),
ceea ce inseamna ca asocierea celor doua productii necesita resurse si de munca si de capital peste disponibilitatile economiei:
LxA + LyA > L
KxA + kyA > k
Situatia acestui Grafic este una imposibila - cel putin vizavi de ipotezele-restrictiile modelului (vezi ipoteza-restrictia economiei inchise ( Diagrama IV.1 / 2).
 (kx) (Ly) LyA LyA' Oy
(kx) (Ly) LyA LyA' Oy
(y)
kxA' (x) A' kyA'
kxA A kyA
(ky)
Ox LxA LxA' (Lx)
Graficul IV.2 (d)
Comentariu grafic:
Odata cu localizarea, si aici, diferita a punctelor A si A' si similar a izocuantelor-perechi (x) si (y) rezulta:
folosirea a OxLxA resurse de munca pentru productia (x), respectiv a LyA'Oy resurse de munca pentru productia (y);
similar pentru resursele de capital: OxkxA pentru productia (x) si respectiv OykyA' pentru productia (y),
ceea ce inseamna ca asocierea celor doua productii necesita resurse si de munca si de capital sub disponibilitatile economiei:
LxA + LyA < L
KxA + kyA < k
Situatia acestui Grafic este una posibila, dar de ineficienta Pareto.
 (Ly) LyA Oy
(Ly) LyA Oy
(kx) (y1) (x3)
(x1) (y2) (x2) C
(y3) B
A (Z3)
(Z1) (Z2)
(ky)
Ox LxA (Lx)
Graficul IV.2 (e)
Comentariu grafic:
Eliminarea ultimelor doua ipoteze conduce la unica asociere posibila si eficienta a productiilor si factorilor, ca in acest Grafic:
pentru fiecare punct A, B, C, . in parte, izocuantele (xi) si (yi) se intersecteazi tangent; astfel aceleasi puncte raman la calitatea de eficienta, din doua puncte de vedere:
intai, ele se situeaza pe aceeasi curba de expansiune comuna;
apoi, ele raman sa functioneze individual pentru ambele productii, lasand resursele de factori sa se insumeze la nivelul disponibilului;
intersectia tangenta a celor doua izocuante, in Caseta EB, lasa loc comuniunii izocosturilor eficiente (Z), pentru cele doua productii, respectiv comuniunii ratei marginale de substitutie intre factori, pentru cele doua productii.
Concluziile modelului
|
2.4.1 Eficienta in combinarea factorilor
Eficienta Pareto in combinarea factorilor este data de comuniunea ratelor marginale de substitutie intre factorii de productie, pentru productiile diferitelor bunuri:
Rms (L k) (x) = Rms (L k) (y)
unde, fireste, avem ratele marginale de substitutie (Rms) intre factorii de productie in explicitarile aratate.
Alte observatii:
Am inlocuit in Graficul IV.2(e) perechea de puncte A&A' cu punctele A, B si C, asociate pe cu totul alt principiu: este pentru a arata ca eficienta Pareto in combinarea factorilor este o stare multipla, iar aceasta acopera, de facto, intregul parcurs al curbei comune de expansiune eficienta pentru productiile (x) si (y).
Starea multipla indica si faptul ca o industrie poate ceda alteia factori de productie pastrand eficienta Pareto pe ansamblu,
ca si faptul ca, incluzand cele doua origini (Ox si Oy) in multimea punctelor de eficienta, aceeasi eficienta Pareto se pastreaza si pentru atribuirea unilaterala a factorilor unei productii, pe seama eliminarii alteia.
2.4.2 Eficienta in nivelul productiilor
Graficul IV.3 se cere considerat in corespondenta grafica cu Graficul IV.2(e).
(y)
 Ox A
Ox A
B
C
O Oy (x)
Graficul IV.3
Comentariu grafic:
Punctele A, B si C, data fiind corespondenta grafica enuntata, preiau coordonatele, in materie de factori (k) si (L), punctelor corespunzatoare din Graficul IV.2 (e) - aici este insavorba de coordonatele punctelor (situatiilor) in materia celor doua productii, (x) si (y).
In prelungirea aceleiasi corespondente, regasim cele doua Origini ale Graficelor IV.2 pozitionate si pe acest grafic.
Curba de fata poarta numele de limita productiilor[3] si identifica combinatiile eficiente Pareto ale productiilor (x) si (y). Discutia asupra formei acestei curbe revine ceva mai jos - ea poate fi comparata cu curba de tip izocuanta.
Daca limita productiilor reprezinta proiectia grafica a curbei de expansiune eficienta a productiilor (x) si (y), de facto corespondenta Graficului IV.3 are loc si cu Graficele IV.2 (c) si (d): pe Graficul de fata incap si "zona imposibila" (Graficul IV.2 (c)), si "zona ineficienta" (Graficul IV.2 (d)). Astfel:
zona "combinatiilor imposibile" - care ar necesita intrari de factori din exteriorul economiei -- se regaseste in mult mai larga multime de puncte aflata la dreapta limitei productiilor;
zona "combinatiilor (posibile dar) ineficiente" - care lasa resurse de factori nefolosite - se regaseste in multimea de puncte aflata la stanga limitei productiilor - intre aceasta si originea Graficului.
Observatii:
Multimea punctelor de eficienta nu este una infinita, dar destul de semnificativa teoretic; si limitele sale se fac insa evidente vizavi de multimile punctelor care arata ineficienta si/sau imposibilitatea combinatiilor productiilor.
Eficienta in nivelul productiei este complet determinata de aceea in combinarea factorilor - astfel criteriul eficientei decurge obligatoriu in aceasta ordine.
Odata cu punctele A, B, C si cu totalitatea punctelor de eficienta - in speta cu multimea de coordonate ale acestora pe cele doua Grafice --, incepem sa observam felul in care se defineste - in conceptia functiei bunastarii - ceea ce se numeste o stare economica - am inceput doar cu valori ale celor doi factori si ale celor doua productii, (x) si (y).
Starile economice eficiente include punctele Ox si Oy, respectiv distribuirea integrala a factorilor pe una singura dintre producctii.
Totalitatea punctelor de eficienta inseamna o totalitate de stari eficiente ale economiei - trecerea economiei dintr-un punct in altul (dintr-o stare in alta) va corespunde eficientei Pareto (a productiei) in dinamica, respectiv in tranzitie.
Tocmai de aceea curba limitei productiei este descrescatoare - identificand fondul pastrat constant al factorilor de productie, distribuit intre productii astfel incat, obligatoriu, cresterea uneia are loc pe seama diminuarii celeilalte. In astfel de conditii, limita productiilor nu figureaza cresterea economica, ci restructurarea productiilor.
Limita productiilor este o curba de forma hiperbolic-concava - in comparatie cu izocuanta sau curba de indiferenta, care sunt hiperbolic-convexe - sau "tipic" concava.
CASETA IV.1 "LIMITA PRODUCTIILOR"
Ea rezulta din hiperbola concava de forma matematica implicita:
ax2 + by2 + c = 0
de valorile lui a si b legandu-se cele doua raze (diametre) ale hiperbolei concave complete ca in figura urmatoare.
 y
y
-x OO x
O
-y
Este drept, astfel, ca aceasta curba nu defineste o functie, decat considerata partial - spre exemplu, pentru zona nord-est, in cazul limitei productiilor, pentru valorile pozitive ale celor doua productii.
Curba tipic concava - partea sau zona nord-est a hipebolei concave:
este descrescatoare, aidoma hiperbolei convexe (izocuantei si curbei de indiferenta);
spe deosebire de hiperbola convexa, hiperbola concava intersecteaza obligatoriu axele rectangualre;
din nou in asemanare cu curba tipic convexa, pe nord-est figureaza cel mai apropriat o relatie de substitutie sau altele similare intre variabile;
regula concavitatii exprima inversa convexitatii: variabila care creste, pe seama celeilalte (in contextul pantei descrescatoare), creste mai incet; variabila care scade scade mai intens.
In fine, pentru a studia regula determinanta eficientei Pareto in productie, sa revedem cele ce se intampla la trecerea - tranzitia - intre puncte de eficienta diferite - buninteles, intre punctele ipotetice A si B, si/sau mai departe: la trecerea din A in B, are loc cresterea productiei (x) pe seama productiei (y), iar aceasta pe seama deplasarii corespunzatoare a factorilor de productie dinspre productia (y) spre productia (x).
Concomitent, insa, trebuie tinut seama si de pozitionarea exacta si limitarea numerica a starilor economice eficiente - in speta, starile economice corespunzatoare punctelor A, B etc. sunt unele si aceleasi; ceea ce inseamna, altfel exprimat, ca trecerea din starea A in starea B este echivalenta trecerii inverse, din B in A, in materia cantitativa a factorilor de productie; difera numai semnul algebric, respectiv cresterea, versus descreserea factorilor pentru o productie, vizavi de cealalta.
Trecerea intre stari economice (eficiente) diferite se aseamana atat redistribuirii, cat si substitutiei - se poate exprima, insa, si prin transformarea unei productii in alta productie, la nivelul societatii economice.
Insfarsit, eficienta in nivelul productiei - echivalenta eficientei transformarilor reciproce intre productii - inseamna comuniunea ratelor marginale de substitutie-transformare intre productii:
(2) Rmt (x y) = Rmt (y x) = Rmt
unde Rmt sunt ratele marginale de transformare cu explicitarile aratate intre nivelurile productiilor, astfel ultima Rmt este unica pentru fiecae dintre punctele de pe curba limitei productiilor - corespunzator, pentru fiecare stare economica eficienta.
2.4.3 Eficienta in consum
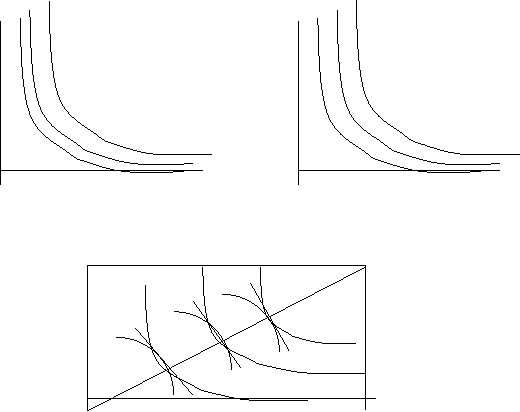
Pana la un punct, eficienta de tip Pareto in zona consumului isi are descriptia aidoma eficientei din zona factorilor si productiei (alti actori, aceeasi piesa / Graficul IV.4). De la utilitatile individuale ale fiecaruia dintre indivizii [A] si [B] se procedeaza la Caseta Edgeworth-Bowley comuna. Tot aidoma rezulta regasirea eficientei multiple de-a lungul diagonalei (Graficele IV.4.b), in punctele exemplificate A, B si, respectiv C - unde, de astadata liniile buget corespunzatoare sunt comune celor doi indivizi. Explicitarea matematica va fi, corespunzator:
(3) Rms (x y) [A]= Rms (x y) [B]
Ceea ce inseamna a treia conditie a eficientei de tip Pareto: eficienta in consum -- egalitatea ratei marginale de substitutie, in consum, intre cei doi indivizi (A si B) si referitor la cele doua bunuri (x si y). Este interesant de observat:
mai intai, ca ecuatia (3) este destul de asemanatoare ecuatiei (1) de mai sus, in sensul definirii substitutiilor corespunzatoare;
mai apoi, ca termenii individuali ai ecuatiei (3) seamana, mai degraba, cu cei din ecuatia (2), a productiilor, in vreme ce descriptia acestei ecuatii este, totusi, alta.
2.4.4 Eficienta in productie si in consum
Ca atare, contextul prezentat aici al functiei bunastarii - limitata deocamdata la obiectivul eficientei Pareto - reclama o coerenta intre productie si consum, care, tot deocamdata, lipseste. Acesta este punctul pana la care demonstratiile din zona productiei si, respectiv, consumului se aseamana. De aici incolo este nevoie de apropierea celor doua substitutii, dar demonstratia din zona consumului va continua intr-o alta ordine.
y y
(a)
(u1A) (u2A) (u3A) (u1B) (u2B) (u3B)
OA x OB x
(b)
x OB
y
A
B
C
y
OA x
Graficele IV.4
Se va considera campul utilitatilor comune (colective) celor doi indivizi (Graficul IV.5), fundamentat pe comuniunea de principiu a substitutiei in consum, definita de ecuatia (3) - o comuniune care priveste deopotriva:
cele doua bunuri (x; y);
cei doi indivizi A; B
 y
y
P
N
M (B3) (u3)
(B2) (u2)
(B1) (u1)
O x
Graficul IV.5
Or, utilitatea comuna (colectiva) isi gaseste, in sfarsit, fundamentarea pe dimensiunile cantitative ale celor doua bunuri (x; y), aidoma limitei productiilor (Graficul IV.3). Poate astfel rezulta comuniunea ratelor marginale de substitutie, atribuite, respectiv, bunurilor (x) si (y), intre productie (limita productiilor) si consum (utilitatea comuna), ca in Graficul IV.6.

y
CE E
(B3) (u3)
(B2) (u2)
(B1) (u1)
O FE x
Graficul IV.6
Comentariu grafic:
Are loc intersectia (inter) tangenta intre limita productiilor (LP) si curba de indiferenta comuna (u3), in punctul E.
Coordonatele acestui punct (xE; yE) asigura cea de a patra si ultima conditie definitorie a eficientei Pareto: eficienta in productie si in consum - echivalenta intre rata marginala de substitutie in consum si rata marginala de transformare intre productii:
(4) Rmt (x y) = Rms (x y [A; B
Explicitarea acestei ultime egalitatieste aceea ca eficienta Pareto reclama - ulterior echivalentei substitutiei factorilor, intre productii, si respectiv substitutiei bunurilor, de o parte in productie, de cealalta in consum - si consonanta productie-consum, in materia ratelor marginale de substitutie.
Tot Graficul IV.6 arata insa o diferenta specifica semnificativa. Descrise (demonstrate) separat, eficienta in productie si cea in consum indicau stari economice multiple. In zona productiei, ar putea fi listata o multitudine de stari economice, definite individual prin cantitati asociate atat ale productiilor celor doua bunuri, cat si ale factorilor implicati (necesitati). In zona consumului, pot fi asociate consumuri ale indivizilor pentru ambele bunuri, in favoarea sau indetrimentul unui si altuia dintre indivizi. In ce priveste eficienta Pareto a productiei si consumului, luate impreuna, aceasta este definita de o singura stare economica - ceea ce echivaleaza:
(i) unui singur nivel al fiecarei productii;
(ii) plus, asocierea de principiu a acestor niveluri;
(iii) unui unic nivel al consumului fiecarui individ in parte;
(iv) iar acesta, in materia fiecarui bun;
(v) consum individual asociat, fireste, productiilor totale individuale;
(vi) unei cantitatidin fiecare factor de productie, implicata in totalitate si pe fiecare productie rezultata.
Observatie. Unicitatea starii economice care ar asigura eficienta Pareto la un moment dat atrage catre modelul Pareto critica, in sensul rigiditatii sale, respectiv neadaptarii la realitate si la nevoia caracterizarii unei economii. Viciul fundamental al gandirii paretiene se localizeaza acolo unde eficienta Pareto exista sau nu exista, lipsind si posibilitatea unei gradualizari, unei evaluari, comparari si, in consecinta, ierarhizari a economiilor si starilor economice de facto. In realitate, rigiditatea eficientei Pareto se prelungeste si in multiplicitatea starilor caracteristice productiei si consumului.
2.4.5 Concluzii extinse
Daca modelul de studiu reducea (initial, metodologic) factorii de productie, productiile (bunurile) si indivizii sociali, la perechi de repere, este acum interesant sa obsevam si ca:
reperele pot fi extinse celelalte la "m" bunuri, "n" indivizi si respectiv "p" factori de productie;
situarile valorice ale lui "m", "n" si "p" pot fi oricae, si mai ales complet independente intre ele,
fara sa fie afectate concluziile modelului de baza, respectiv concluziile extinse ale modelului inseamna ca eficienta de tip Pareto inseamna:
egalitatea ratelor tehnice de substitutie ale celor "p" factori;
egalitatea ratelor marginale de transformare, in productie, pentru cele "m" industrii (bunuri finale);
egalizarea:
(3a) ratelor marginale de substitutie, in consum, ale celor "m" bunuri, pentru cei "n" indivizi;
(3b) la nivelul valorii ratei marginale de transformare, in productie, corespunzatoare.
Observatii:
concluziile extinse ale modelului ies din judecata grafica de baza, devenita imposibila;
aceleasi concluzii finalizeaza, totusi, nu numai o parte a intregului model Pareto, ci chiar o parte din ceea ce priveste eficienta Pareto - am numit modelul static.
Modelul dinamic
Din demersul de mai sus am inteles atat conceptul de stare economica - asociata modelului static --, cat si pe acela de tranzitie - care urmeaza sa capete contur in paragraful de fata. Modelul dinamic priveste, astfel, trecerea (tranzitia) intre doua stari economice date, iar aceasta presupune concomitent doua (alte) criterii (dinamice) de tip Pareto:
(i) imbunatatirea starii cel putin unui individ;
(ii) neafectarea (bineinteles negativa) a starii economice a niciunui individ.
Evolutia gandirii economice, pe partea bunastarii, de la Pareto incoace nu a adus contraziceri principiale ale modelului Pareto, ci numai oarecari critici si adaugiri, n special in zona dinamica a modelului. Nume ca C.K. Lancaster sau R.G. Lipsey flexibilizeaza cele doua restrictii, admitand pastrarea in vizor a bunastarii si in conditiile afectarii partiale a starii economice initiale.
Rezulta astfel asanumita teorie "second best" - noua stare economica este admisa pentru caderea a cel putin o data initiala. Noutatea conceptului este data de ideea de bun simt ca bunastarea nu poate fi considerata complet sau fundamental distrusa de / printr-o simpla perturbare -- oricare tranzitie poate fi acceptata:
si sa produca concomitent imbunatatiri si inrautatiri ale starii economice initiale;
si sa aduca concomitent schimbare, dar si pastrare a datelor starii de baza.
Reusita noii teorii are loc exact acolo unde lipsea complet din conceptia paretiana: aduce oportunitatea de a compara si ierarhiza intre ele doua sau mai multe stari economice diferite.
Observatie: Si odata cu completarea adusa de modelul dinamic ramanem cantonati intr-o parte a studiului bunastarii, am numit functia obiectiv a eficientei - buninteles insuficienta definirii bunastarii. Cealalta functie obiectiv a bunastarii este echitatea.
Conceptul de echitate
Studiul echitatii in economie este relativ nou, adica de varsta postbelica. Daca eficienta raspundea la intrebarile "ce si cum se produce ?", echitatea va raspunde la intrebarea "pentru cine se produce ?".
Cateva repere teoretice
Egalitarismul isi fixeaza drept obiectiv egalizarea bunastarii, si mai intai a veniturilor, parvenind pana la confuzia celor doua. O dificultate normativa consta in complementarea si preliminara evaluare sociala, nu tocmai simplu de realizat. In al doilea rand, afara de faptul (usor de inteles) ca egalitarismul era usor de reperat de catre curentele socialiste de gandire economica, se reproseaza acestei viziuni ceea ce se reproseaza curentului socialist in totalitatea sa: de-motivarea muncii si ridicarii calificarii si performantelor individuale.
Constiinta sociala defineste mobilizarea voluntara la contributia in folosul bunastarii altora - incercandu-se aici diferentierea fata de un principiu operand in aceeasi directie in cadrul politicilor fiscale.
"Under-dog" standard focalizeaza studiul asupra celor mai mici dintre venituri si asupra starii de precaritate economica - aceste venituri sunt raportate concomitent la nevoile elementare si la celelalte venituri obtinute efectiv in economie.
Reperul "inter-generatii" opereaza in zona deciziei politice pentru un alt criteriu indeajuns de rezonabil - repartizarea bunastarii reale (create astazi) intre prezent si viitor, pentru obiectivele profitabilitatii, investitiilor si astfel distribuirea-redistribuirea avutiei pe cele doua directii.
Echitate si eficienta in modelul Pareto
Reluam descriptia de la Graficele IV.4, de mai sus, explicitand prin Caseta Edgeworth-Bowley ecuatia (3) a modelului. Eficienta Pareto se dovedise, in final, punctiforma (Graficul IV.6 si ecuatia 4), in conditiile unei libertati de miscare intre punctele OA si OB (Graficul IV.4) - ceea ce semnifica, de facto, indiferenta criteriului eficientei fata de distribuirea utilitatilor intre cei doi indivizi.
Or, satisfacerea concomitenta a criteriilor eficientei Pareto si echitatii ar presupune - indiferent de criteriul de echitate aplicat - restrangerea la o singura (unica) combinatie distributiva a bunurilor (c) si (f) intre indivizii [A] si [B]. O astfel de probabilitate se restrange la minimum teoretic posibil.
Indiferent de criteriul aplicat, adica intelegand aici abaterea, mai mult sau mai putin, de la principiul (obiectivul) egalitatii (criteriul egalitarist, considerat in paragraful anterior). Cu slte cuvinte, eficienta Pareto poate considera pana si ipostazele in care unul dintre indivizi isi insuseste integral utilitatile existente, nelasandu-i nimic in acest sens celuililalt. Teoretic, chiar o astfel de situatie poate fi adevarata combinatie eficienta de consumuri.
Nu omitem insa ca am asociat aici echitatea unui model al eficientei considerata preliminara, astfel prioritara sau primordiala. In acest model, eficienta porneste de la o arie larga, iar echitatea, aparent, o restrange pe aceasta. Este insa posibil ca, reconsiderand semnificatia Graficului IV.6 (la care astfel revenim), sa re-descoperim si libertatea de miscare a echitatii, vizavi de eficienta Pareto. Cu cat coboram nivelul utilitatii colective, de la u3 la u2 si, respectiv, u1, cu atat:
revenim la stanga limitei productiilor, adica in zona (posibila, dar) ineficienta,
multiplicand, insa, gradual aria echitabila. Avem aici in vedere atat multiplicarea progresiva a lungimii curbelor (u2) si respectiv (u1), la stanga curbei limitei productiilor (LP), in Graficul IV.6, cat si individualizarea consumurilor indivizilor [A] si [B], pe diagonalele Graficelor IV.4, catre fiecare dintre cele doua origini.
Ca atare, modelul Pareto descopera incompatibilitatea dintre eficienta si echitate, drept un principiu dupa care:
reconcilierea lor revine la minimum de probabilitate;
dimpotriva, aria echitatii recastiga teren prin chiar indepartarea graduala (progresiva) de satisfacerea deplina a eficientei Pareto.
Inegalitatea economica
Iesind din aria modelului Pareto, regasim un alt concept nou, de varsta postbelica[4]. Conceptul nu se confunda cu chestiunile legate de echitate - nici macar chestiunile de detaliu, asa cum vom vedea ceva mai jos.
O legatura mai trainica a conceptului de inegalitate economica - decat aceea cu echitatea - este pastrata cu distributia venitului national (Lectia VII)[5] - inegalitatea manifestandu-se prioritar in zona retribuirii factorului munca (salariilor), decat in zonele retribuirii celorlalti factori de productie (renta, profit sau dobanda). Aceasta desi, paradoxal, retribuirea factorului munca pastreaza - in venitul national - o pondere mai mult decat importanta si chiar cu tendinta de crestere, pe perioade indelungate, in detrimentul retribuirii celorlalti factori.
Oricum, manifestarea inegalitatii, ca problema a economiei contemporane - in afara sau chiar impotriva unor gandiri politice --, este data de accentuarea inegalitatilor de venit si prosperitate, ca un alt trend al aceleiasi economii moderne in general.
Cauze ale inegalitatii
Pot fi listate cateva cauze fundamentale, in domeniu, lista putand cntinua si in concretizaarea unor situatii date:
(i) diferentierile in marimea si valorificarea proprietatii (proprietatilor);
(ii) comportamentul pietei factorilor de productie, individualizat de la factor la factor - piata pe care forta de munca prezinta realmente un comportament specific;
(iii) in aceasta din urma zona, mai vorbim si de o diferentiere a capacitatilor, calificarilor si abilitatilor individuale;
(iv) rezultatele diferentiate ale politicilor de crestere economica.
Studiul inegalitatii
Studiul in sine al inegalitatii se dovedeste si el, dintru inceput, o chestiune complexa. R.M. Titmus vorbeste despre o "neadecvare a datelor". Problema de inceput este considerarea bazei de date:
unitatea taxabila;
venitul total taxabil;
legea Pareto - dupa care exista regularitatea atribuirii unui anume venit unui anumit numar de indivizi.
In continuare, studiul cauta (fireste) depistarea gradului general de inegalitate-egalitate sociala, in baza datelor inmagazinate pe categorii - de venit si, respectiv, de indivizi.
Observatii: Sunt eliminate oricare alte referiri ale partajarii populatiei sau criteriilor de partajare sau clasificare intre indivizi.
Reprezentativ pentru studiul inegalitatii economice este instrumentul numit curba Lorenz (Graficul IV.7).
 =venituri cumulate 100%=
=venituri cumulate 100%=
Y A
(0) (a) (b)
O Z = indivizi beneficiari (100%)=
Graficul IV.7
Comentariu grafic:
Abscisa se considera acoperita de indivizii beneficiari ai venitului total din economie, in ordinea crescatoare a veniturilor: primul individ, "asezat" in vecinatatea Originii, are venitul cel mai mic, urmatorul are un venit mai mare si asa mai departe, astfel incat in dreptul punctului A se regasesc veniturile individule cele mai ridicate.
Ordonata este orientativa pentru venitul total -- cumulat, la nivelul societatii - dar venitul. In realitate, insa, venitul se cumuleaza in triunghiurile formate intre punctele O, A si Z -- si vorbim de o multiplicitate de triunghiuri OAZ, pentru ca:
diagonala rectilinie OA departajeaza triunghiul normal, respectiv starea teoretic limita, a egalitatii perfecte intre veniturile individuale - primul individ de pe axa OZ castiga egal cu toti ceilalti "insirati" pe axa, iar numaratoarea oprita la oricare individ (i / i< n ) ar lasa in urma cresterea proportionala a venitului, in raport cu numarul de indivizi;
dimpotriva, "abaterea" diagonale OA prin (a), (b) etc. lasa in spatiul (triunghiurile) din dreapta diagonalei un venit cumulat mai mic pentru primii indivizi si respectiv mai mare pentru urmatorii;
toate diagonalele isi regasesc insa bransarea in punctele O si A - aceasta inseamna considerarea integrala a venitului cumulat, ca raportat la totalitatea (pana la ultimul) a indivizilor.
Diagonala rectilinie OA corespunde inegalitatii cotate zero - egalitatii perfecte a venitului. Dimpotriva, diagonala OaA capata un grad de inegalitate, iar diagonala ObA un grad de inegalitate inca mai mare.
Se poate observa si cu ochiul liber gradul de inegalitate, si chiar compararea diferitelor grade de inegalitate intre ele: el este cu atat mai mare cu cat triunghiul O(a, b, . )AZ revine mai mic, din cauza diagonalei mai curbe. La nivel de specialitate, aria acestor triunghiuri presupune un calcul integral. Finalizarea calculului gradului de inegalitate presupune insa reportarea suprafetei triunghiului considerat la suprafata totala OAZ, corespunzatoare inegalitatii unle (egalitatii perfecte). Rezulta astfel valori subunitare si abstracte, respectiv coeficientii Ginni (Cg):
Cg = ∫ (Oa,b, . AZ) / ∫(OAZ)
care indica un grad de inegalitate cu atat mai mare cu cat valoarea lor este mai mica, deci apropiata de zero. Intervalul valoric al coeficientilor este, astfel, zero, pentru inegalitatea perfecta, si unu, pentru egaliatea perfecta, respectiv inegalitatea zero - in realitate, ceea ce exprima direct coeficientii Ginni, prin valoarea lor, este egalitatea, si indirect inegalitatea economica.
Politici de egalizare a veniturilor
In incheierea si a dezbaterii despre inegalitate economica, si a lectiei noastre despre functia bunastarii, enumeram cateva repere ale politicilor de combatere a inegalitatii - egalizare a veniturilor.
Mai intai, mai uzitata si mai apropiata de realitatea zilei este, in aceasta privinta, fiscalitatea. Aceasta procedeaza la:
impozitarea progresiva pe venituri;
taxa pe valoarea adaugata - impozitarea tipic indirecta - care vizeaza cheltuieli specifice, vizavi de veniturile in care se implica factorii de productie in totalitate;
diferentierea impozitarii intre sectoarele public si privat etc.
In al doilea rand, si, din pacate, tot la indemana exclusiva a statului opereaza cheltuielile guvernamentale, care au drept rezultat alocari si beneficii banesti in primul rand directe, dar si indirecte.
|
Concepte: caseta Edgeworth-Bowley (EB) |
eficienta Pareto (a productiei) in dinamica |
stare economica |
|
cheltuieli guvernamentale |
egalitarism |
teoria "second best" |
|
coeficientii Ginni (Cg) |
fiscalitate |
transformarea unei productii in alta productie |
constiinta sociala "under-dog" standard
|
criterii (dinamice) de tip Pareto |
utilitati comune (colective) |
|
|
curba Lorenz |
functia bunastrarii (Sw) |
|
|
curba tipic concava |
grad de inegalitate |
|
|
echitate |
indivizii sociali |
|
|
eficienta |
inegalitate economica |
|
|
eficienta in consum |
limita productiilor |
|
|
eficienta in nivelul productiei |
modelul static |
|
|
eficienta in productie si in consum |
optimul de tip Pareto |
|
|
eficienta Pareto a combinarii factorilor de productie |
reperul "inter-generatii |
|
Chestiuni:
Explicati substratul definitoriu al functiei bunastarii de tip "Pareto".
Explicati semnificatia economica a unicitatii ratei marginale de substitutie a factorilor de productie pentru o economie:
(2a) cu numai doua productii;
(2b) cu mai mult de doua productii.
Care este corelatia grafica intre (a) eficienta combinarii factorilor si (b) limita productiei ?
Explicati caracterul "limita" al egalitatii intre:
(4a) rata marginala de substitutie, in consum si
(4b) rata marginala de transformare, in productie, pentru mjodelul eficientei de tip Pareto.
ANEXA RECAPITULATIVA
Recapitulare pe exemple grafice
Curbele productiei pe termen scurt
Figura 1 explica cresterea limitata a productiei pe termen scurt, urmare cresterii factorilor variabili ( capitalul variabil, kv, si munca, L).
Notatii:
L - forta de munca angajata
Q - productia (propriuzisa, totala)
Qa - productivitatea medie:
Qa = Q / L
Qm - productivitatea marginala:
Qm = DQ /D L
 (Q; Qa; Qm)
(Q; Qa; Qm)
QB' B'
QA' A' (Q)
A (Qm)
B
(Qa)
O FVA FVB (FV)
Figura 1
Explicatii:
OA' - zona extensiva: crestere accelerata a productiei (Q), determinata de cresterea (panta crescatoare a) productivitatii medii. Intelesul de "extensiv" este insa acela al factorilor variabili (abscisa) carora productia si cresterea ei li se datoreaza in cea mai mare parte.
A'B' - zona intensiva: incetinirea cresterii productiei totale, in legatura cu (determinata de) panta descrescatoare a productivitatii medii. Intelesul de "intensiv" este unul indirect: nu mai avem regula de mai sus a intelesului de "extensiv", in sensul contributiei factorilor variabili.
B'(Q) - zona neeconomica: cresterea productiei s-a oprit, urmare cresterii factorilor variabili, dar si determinat de depasirea, in aceeasi oridine, a maximelor celor doua productivitati, cea marginala si cea medie.
Izocuanta-izocost & curba de indiferenta-linie buget
 k y
k y
(u3)
(u1)
(Q3) (u2)
(Q2)
(Z2) (Z3)
(Q1) (B1) (B2) (B3)
(Z1)
O L O x
(a) (b)
Figura 2
|
Figura 2 (a) arata: (i) substitutia intre cei doi factori de productie, capital (k) si munca (L), pe termen lung, pentru: productie - izocuante; costuri - izocost. (ii) curba de expansiune a productiei, in conditii eficiente (costuri minime). Notatii: (Q1, 2, 3) -- izocuante (Z1, 2, 3) - izocost L - forta de munca k -- capital |
Figura 2(b) arata: (i) substitutia intre doua bunuri (x, y), in consum; (ii) niveluri ale utilitatii celor doua bunuri substitute; (iii) bugetul maxim de afectat fiecarei utilitati aduse de cele doua bunuri substitute. Notatii: (u1, 2, 3) - curbe de indiferenta (B1,2,3) - linii buget x, y - bunuri substitute |
|
Observatii: izocuantele sunt izomorfe si paralele; izocosturile sunt izomorfe, dar nu neaparat paralele intre ele; curba de expansiune nu este, neaparat, rectilinie |
Observatii: curbele de indiferenta sunt izomorfe si paralele liniile buget sunt izomorfe si nu neaparat paralele |
|
izocosturile nu sunt unice, fata de curba izocuanta, ci se distinge izocostul eficient |
linia buget nu este eficienta, ci unica, vizavi de curba de indiferenta. |
|
panta izocostului depinde de raportul de preturi intre factori, pe piata |
panta liniei buget depinde (si ea) de raportul de preturi intre bunuri, pe piata |
Concluzii comune:
Proprietatile curbelor tipic convexe:
(i) caracter descrescator, pe cadranul nord-est (valori pozitive ale variabilelor);
(ii) panta variabila (nu sunt rectilinii);
(iii) referinta la substitutii.
Substitutia este:
(a) pentru curbele tipic convexe (izocuante; curbe de indiferenta):
(i) neomogena (nu sunt rectilinii);
(ii) maxima, la mijlocul curbei, descrescatoare, catre extremitatile curbei;
(b) pentru curbele rectilinii (izocost; linie buget): omogena.
Functiile: cererii & ofertei
 P P
P P
(D) (S)
O Q O Q
Figura 3 Figura 4
Notatii:
P - pretul bunului
Q - cantitatea bunului:
Cantitatea
ceruta (Figura 3) oferita (Figura 4)
Observatie comuna: Determinanta (exogenitatea) apartine (pentru amble functii) pretului bunului asupra cantitatii (de ambele feluri).
|
I |
Comportamentul functiei: |
|
|
|
cererii (D) |
ofertei (S) |
|
A |
Linie: |
|
|
|
curba: Q=Q(P) |
|
|
|
dreapta: Q=aP+b |
|
|
|
descrescatoare -- bunuri ordinare |
crescatoare (exclusiv) |
|
|
crescatoare -- bunuri speciale (Giffen & Veblen) |
|
|
B |
Elasticitate (pe zone): |
|
|
|
inelasticitate perfecta -- Q nu variaza, indiferent de variatia lui P |
|
|
|
(2) inelasticitate -- variatie mai mica (relativ) a elasticitatii fata de variatia pretului |
|
|
|
(3) elasticitate unitara -- variatia in aceeasi masura a cantitatii si a pretului |
|
|
|
(4) elasticitate (propriuzisa) -- variatia lui P induce variatii relativ mai mari ale cantitatii |
|
|
|
(5) inelasticitate perfecta -- Q variaza, indiferent de variatia sau nonvariatia lui P |
|
|
C |
Bunuri speciale: Giffen & Veblen (abatere de la legea cererii) |
Nicio referire la bunuri speciale (nu exista abateri de la respectarea legii ofertei) |
|
II |
Surplusul: |
|
|
|
consumatorului (Sc) |
producatorului (Sp) |
 P P
P P
(Sc) (D) (S)
P1 A P1 B
(Sp)
O Q1 (D) Q O Q1(S) Q
Figura 5 Figura 6
Aria triunghiului:
|
P1PA: |
P1PB: |
|
la stanga curbei |
la stanga curbei |
|
deasupra nivelului pretului considerat |
sub pretul considerat |
Observatie: Cresterea pretului P1 va reduce surplusul consumatorului si va creste surplusul producatorului.
Echilibrul cerere-oferta
 P P
P P
(S)
(D)
E1 E2
(D)
(S)
O Q O Q
Figura 7 Figura 8
stabil (ordinar) nestabil (bunuri Giffen-Veblen)
Recastigarea echilibrului cerere-oferta (modelul "cobweb")
 P
P
(S)
(D)
O Q
Figura 9
Observatie: Convergenta-divergenta miscarii de reechilibrare este determinata de forma-panta curbelor cererii (elastice, pentru convergenta) si ofertei (inelastice, pentru convergenta).
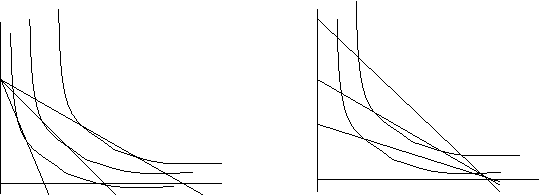
Cererea si utilitatea - compunere grafica
 Qy Qy
Qy Qy
(B3)
(U1) (U3) (a) (U1) (U3)
(B2) C
(U2) (U2)
A B C
(B1) B
(B1) (B2) (B3) A
O QA QB QC Qx O Qc QB QA Qx
 Px Px
Px Px
A (Dx)
B (b)
C A
B
(Dx) C
O QA QB QC Qx O Qc QB QA Qx
Figura 10
|
Reducerea pretului bunului (x), in raport cu pretul bunului (y). |
Cresterea pretului bunului (x), in raport cu pretul bunului (y). |
|
|
|
7. Caseta Edgeworth-Bowley (EB) si curba limitei productiilor
 kx ky
kx ky
(x3) (y3)
(x2) (y2)
(x1) (y1)
Ox Lx Oy Ly
(a) (b)
Figura 11
Doua productii (bunuri), (x) si (y), cu curbele de expansiune, principial diferite.
 (Ly) LyA Oy
(Ly) LyA Oy
(kx) (y1) (x3)
(x1) (y2) (x2) C
(y3) B
A (Z3)
(Z1) (Z2)
(ky)
Ox LxA (Lx)
Figura 12
(1) Caseta EB indica:
(i) economia inchisa - intre cele doua perechi de axe ale factorilor de productie, aferente fiecarei productii in parte;
(ii) comuniunea curbei de expansiune - demonstrata, de la situatia initiala, diferita pe productii;
(iii) aceeasi curba de expansiune comuna drept comuniunea punctelor de eficienta Pareto;
(iv) aceeasi eficienta Pareto pentru comuniunea curbelor izocost eficiente, astfel a ratelor marginale de substitutie inter-factori, pentru cele doua productii, (x) si (y).
Observatie: Caseta EB se poate aidoma construi pentru curbele de indiferenta si liniile buget ale bunurilor (x) si (y), in consum. Va lipsi aici numai curba de expansiune, care nu cunoaste corespondent in zona consumului si utilitatilor.
 (y)
(y)
Ox A
B
C
O Oy (x)
Figura 13
Limita productiilor este proiectia curbei de expansiune comune pe graficul productiilor (x) si (y), fundamentate pe fondul comun al resurselor de factori de productie. Semnificatia acestei curbe este pozitionarea fixa a perechilor de productii care se asociaza, in conditiile utilizarii (consumului productiv al) intregului fond de resurse. De-a lungul curbei, productiile (x) si (y) sunt imaginate a fi restructurate eficient, astfel:
Rmt (x y) = Rmt (y x) = Rmt
unde Rmt este rata marginala de transformare intre productii, la suprafata economiei.
Curba tipic convexa (izocuanta sau curba de indiferenta) si curba tipic concava (limita productiilor)
Originea celor doua curbe este hiperbola:
 y y
y y
-x O x -x O x
-y -y
(a) (b)
Figura 14
|
convexa |
concava |
Redactare matematica (in forma implicita):
|
axy + b = 0 |
ax2+by2+c=0 |
|
Niciuna dintre cele doua variabile nu se anuleaza -- curba nu intersecteaza axele. |
Curba intersecteaza obligatoriu ambele axe. |
|
|
Parametrii (a) si (b) sunt legati de cele doua raze (diametre) ale hiperbolei. |
Caracteristici comune:
Hiperbolele capata valoare de functii prin restrangere la cadranul nord-est (valori superioare ale variabilelor);
pe aceasta zona, ambele functii sunt descrescatoare
si apropriate relatiilor de tip substitutie.
y y

O x O x
(a) (b)
Figura 15
Separarea regulilor dinamice:
Pe fondul comun al pantei descrescatoare:
|
Variabila care creste - pe fondul scaderii celeilalte - creste mai repede decat scade cealalta. |
Variabila care creste - pe fondul scaderii celeilalte - creste mai lent decat scade cealalta. |
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2026 - Toate drepturile rezervate -| |
|
|
|||
|
|||
Referate pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








