
| Biologie | Botanica | Chimie | Didactica | Fizica | Geografie |
| Gradinita | Literatura | Matematica |
Matematica
|
|
Qdidactic » didactica & scoala » matematica Transformari geometrice in plan - translatia, omotetia si simetria - clasa a IX-a, geometrie |
Transformari geometrice in plan - translatia, omotetia si simetria - clasa a IX-a, geometrie
Transformari geometrice in plan - translatia, omotetia si simetria
Clasa a IX-a
Geometrie
Trecerea de la conceptele teoretice la aplicatii practice este intotdeauna greoaie. Mai mult, pentru a implica toti elevii in mod direct la rezolvarea aplicatiilor practice, trebuie lucrat simultan cu acestia. Acest lucru se dovedeste a fi greu realizabil in maniera clasica de lucru.
Utilizarea calculatorului permite crearea unui mediu virtual, un asa numit simulator, in care fiecare elev poate parcurge etapele de rezolvare ale problemei respective, sau poate vizualiza fenomenul respectiv intr-o maniera interactiva existand premisele unei intelegeri mai rapide si mai temeinice a fenomenului respectiv.
In cadrul acestei lectii, elevul va parcurge urmatoarele momente:
momentul m1 :
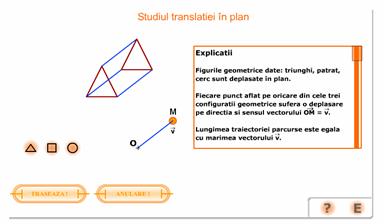
Se arata
ca figurile geometrice triunghi,
patrat, cerc sunt deplasate in plan, pe directia si sensul
vectorului ![]() , lungimea traiectoriei parcurse fiind egala cu
marimea vectorului
, lungimea traiectoriei parcurse fiind egala cu
marimea vectorului ![]() .
.
Se studiaza pentru figurile geometrice date,
translatiile de vectorul ![]() , variabil ca marime, directie si sens. Se
poate studia cazul in care M se confunda
cu O.
, variabil ca marime, directie si sens. Se
poate studia cazul in care M se confunda
cu O.
Se arata ca imaginea unui triunghi printr-o translatie este un triunghi, imaginea unui patrat printr-o translatie este un patrat si imaginea unui cerc printr-o translatie este un cerc.
momentul m2 :
Se arata ca daca intr-un trapez diagonalele sunt congruente, atunci trapezul este isoscel.

momentul m3 :
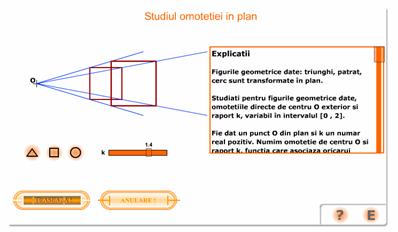
Se arata ca figurile geometrice triunghi, patrat, cerc sunt transformate in plan
|
Se studiaza pentru figurile geometrice date, omotetiile directe de centru O exterior si raport k, variabil in intervalul [0 , 2]
Se arata ca imaginea unui triunghi printr-o omotetie este un triunghi, imaginea unui patrat printr-o omotetie este un patrat si imaginea unui cerc printr-o omotetie este un cerc.
momentul m4 :
Se arata ca figurile geometrice triunghi, patrat, cerc sunt simetrice fata de punctul O, fix in plan.
Se studiaza pentru figurile geometrice date, a caror pozitie in plan este variabila, simetriile fata de punctul fix M.
Se arata ca imaginea unui triunghi printr-o simetrie centrala este un triunghi, imaginea unui patrat printr-o simetrie centrala este un patrat si imaginea unui cerc printr-o simetrie centrala este un cerc.

momentul m5 :
Se arata ca figurile geometrice triunghi, patrat, cerc sunt simetrice fata de dreapta d, fixa in plan.
Se studiaza pentru figurile geometrice date, a caror pozitie in plan este variabila, simetriile fata de simetriile fata de dreapta fixa d.
Se arata ca imaginea unui triunghi printr-o simetrie axiala este un triunghi, imaginea unui patrat printr-o simetrie axiala este un patrat si imaginea unui cerc printr-o simetrie axiala este un cerc.

momentul m6 :
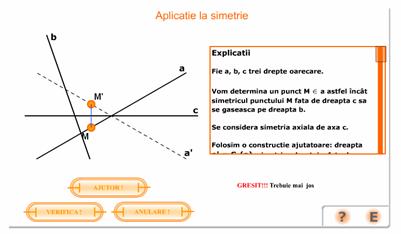
Se considera a, b, c trei drepte oarecare.
Se va determina un
punct ![]() astfel incat
simetricul punctului M fata
de dreapta c sa se
gaseasca pe dreapta b.
astfel incat
simetricul punctului M fata
de dreapta c sa se
gaseasca pe dreapta b.
Comentarii finale
![]()
Se asteapta de la materialul prezentat cu ajutorul calculatorului sa aduca mai degraba un plus de intuitivitate pentru continutul prezentat prin:
introducerea notiunilor in mod vizual si interactiv;
facilitarea descoperirii utilitatii practice a unor notiuni teoretice
manifestarea curiozitatii si a imaginatiei in rezolvarea de probleme
manifestarea tenacitatii, a perseverentei si a unei capacitati de concentrare pe problema
dezvoltarea unei gandiri deschise, creative si a unui spirit de obiectivitate si impartialitate
formarea obisnuintei de a recurge la concepte si metode matematice in abordarea unor situatii cotidiene sau pentru rezolvarea unor probleme practice
formarea motivatiei pentru studierea matematicii ca domeniu relevant pentru viata sociala si profesionala
formularea de sarcini de prelucrare variata a informatiilor in scopul formarii competentelor vizate de programa scolare
alternarea prezentarii continuturilor cu moduri variate de antrenare a gandirii
punerea elevului in situatia ca el insusi sa formuleze sarcini de lucru adecvate
obtinerea de solutii sau interpretari variate pentru aceeasi unitate informationala
folosirea unor metode care sa favorizeze relatia nemijlocita a elevului cu obiectele cunoasterii prin recurgere la modele concrete
insusirea unor metode de informare si de documentare independenta care ofera deschiderea spre autoinstruire si invatare continua
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2026 - Toate drepturile rezervate -| |
|
|
|||
|
|||
|
|||
Proiecte pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








