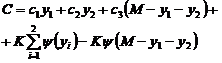| Biologie | Botanica | Chimie | Didactica | Fizica | Geografie |
| Gradinita | Literatura | Matematica |
Matematica
|
|
Qdidactic » didactica & scoala » matematica Test programare liniara |
Test programare liniara
TRUE/FALSE
1.
Exista probleme de programare liniara care sa nu poata fi exprimate in forma standard.
ANS: F
2. Orice problema de minimizare poate fi transformata intr-o problema de maxim.
ANS: T
3.
Orice problema de minimizare poate fi transformata intr-o problema de maxim, pe baza relatiei,
![]()
ANS: T
4.
In exprimarea matriceala, o
problema de programare liniara in forma canonica este descrisa astfel.
Determina vectorul ![]() Rn
care maximizeaza
Rn
care maximizeaza
![]()
cu restrictiile
![]()
![]()
ANS: T
5.
In exprimarea matriceala, o
problema de programare liniara in forma canonica este descrisa astfel.
Determina vectorul ![]() Rn
care maximizeaza
Rn
care maximizeaza
![]()
cu restrictiile
![]()
![]()
ANS: F
6.
Functia obiectiv a unei
probleme de programare liniara este ![]() .
Fie k o constanta. Graficul ecuatiei
.
Fie k o constanta. Graficul ecuatiei
![]()
este un hiperplan.
ANS: T
7. Intersectia unui numar finit de multimi convexe (daca nu este multimea vida) este multime concava.
ANS: F
8. Multimea tuturor combinatiilor convexe definite pe un set finit de puncte din Rn este convexa.
ANS: T
9. Fie o problema de programare liniara in forma canonica in care matricea A are m linii si n+m coloane. Daca rangul matricei A este m, rezulta ca vectorii care formeaza liniile lui A sunt liniar independenti. Rezulta ca sistemul constrangerilor nu contine ecuatii redundante.
ANS: T
10. Fie P problema de programare liniara in forma canonica si S multimea solutiilor admisibile ale lui P. Orice solutie de baza si admisibila a lui P este punct extrem al lui S si, reciproc, orice punct exterm al lui S este solutie de baza si admisibila a lui P.
ANS: T
11. Pasul al doilea al metodei simplex presupune verificarea criteriului de optimalitate.
ANS: T
12. Regula Bland. Alege drept coloana pivotala prima coloana (cea cu indicele minim) cu element nul in linia obiectiv.
ANS: F
13. Fie P problema de programare liniara in forma standard. Problema duala asociata problemei duale a lui P este P.
ANS: T
14.
Fie problema de programare liniara,
maximizeaza ![]()
cu restrictiile,
![]()
![]() nerestrictionat
nerestrictionat
Forma duala este problema de programare liniara,
maximizeaza ![]()
cu restrictiile,
![]()
ANS: F
15.
Fie problema primala de programare liniara,
maximizeaza ![]()
cu restrictiile,
![]()
Pentru fiecare i, ![]() este
interpretat ca stocul maxim disponibil din cea de-a i-a resursa.
este
interpretat ca stocul maxim disponibil din cea de-a i-a resursa.
ANS: T
16. Membrul stang al celei de-a j-a constrangeri a problemei duale semnifica valoarea totala a intrarilor utilizate pentru producerea unei unitati din cea de-a j-a iesire.
ANS: T
17. Daca problema primala/duala are o solutie admisibila si functia obiectiv are o valoare optima finita, atunci problema duala/primala are o solutie admisibila cu aceeasi valoare obiectiv.
ANS: T
18.
Consideram disponibil
istoricul randamentelor procentuale pe m perioade de timp pentru fiecare
actiune dintr-un grup de n actiuni si notam cu ![]() ,
randamentul actiunii i in perioada j;
,
randamentul actiunii i in perioada j; ![]() ,
fractiunea investita in actiunea i, astfel incat
,
fractiunea investita in actiunea i, astfel incat ![]() ;
;![]() ,
varianta actiunii i;
,
varianta actiunii i;![]() ,
covarianta dintre actiunile i si k. Portofoliul este definit de
fractiunile de investitii
,
covarianta dintre actiunile i si k. Portofoliul este definit de
fractiunile de investitii ![]() .
.
Randamentul asteptat al
portofoliului este dat prin ![]()
ANS: T
19.
In general, tehnicile de rezolvare a problemelor de optim (nu neaparat liniare) nu sunt iterative.
ANS: F
20. Tehnicile de cautare directa utilizeaza comparatii ale valorilor functiei de optimizat in puncte de test.
ANS: T
21.
Problema RISCMIN1M (pentru a determina portofoliul optim cu valoarea tinta pentru randament data de Rp) poate fi exprimata in termenii unei probleme de optimizare fara restrictii, astfel
Minimizeaza ![]()
ANS: T
22.
Fie setul de restrictii ale unei probleme de programare liniara,
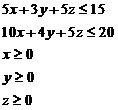
Punctul ![]() apartine
multimii solutiilor admisibile ale problemei.
apartine
multimii solutiilor admisibile ale problemei.
ANS: T
23.
Fie problema de programare liniara in forma canonica,
Maximizeaza ![]()
cu restrictiile
![]()
![]()
si astfel incat ![]() .
.
Determinarea unei solutii
de baza admisibile poate fi realizata prin metoda in doua faze. In prima faza a
metodei, pentru obtinerea unei solutii de baza fezabile, sunt introduse m
variabile artificiale, notate cu ![]() ,
obtinandu-se problema,
,
obtinandu-se problema,
Maximizeaza ![]()
cu restrictiile
![]()
![]()
si astfel incat ![]() .
.
ANS: F
24.
O varianta pentru a determina portofoliul optim este de a fixa o valoare tinta pentru randament, de exemplu de Rp procente, si de a minimiza functia risc. O varianta a acestei probleme, RISCMIN1M poate fi exprimata prin
Minimizeaza ![]()
ANS: T
MULTIPLE CHOICE
1.
Fie problema de programare liniara
maximizeaza ![]()
cu restrictiile
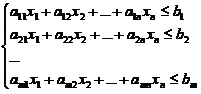
![]()
Problema definita mai sus este
|
a. |
in forma standard |
c. |
in forma oarecare |
|
b. |
in forma canonica |
d. |
nici una din celelalte variante prezentate |
ANS: A
2.
Fie problema de programare liniara
maximizeaza (*) ![]()
cu restrictiile
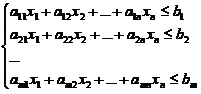
![]()
Functia definita in (*) este numita
|
a. |
functie de selectie |
d. |
functie de dilatare |
|
b. |
functie obiectiv |
e. |
nici una din celelalte variante prezentate |
|
c. |
functie de contractie |
|
|
ANS: B
3.
Fie problema de optimizare
Minimizeaza ![]()
cu restrictiile
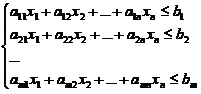
![]()
Problema definita mai sus este
|
a. |
de programare liniara in forma standard |
c. |
nici una din celelalte variante prezentate |
|
b. |
de programare liniara in forma canonica |
|
|
ANS: C
4.
Fie problema de programare liniara
maximizeaza ![]()
cu restrictiile
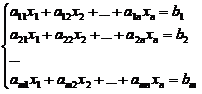
![]()
Problema definita mai sus este
|
a. |
in forma standard |
c. |
in forma oarecare |
|
b. |
in forma canonica |
|
|
ANS: B
5.
Fie problema de optimizare
minimizeaza ![]()
cu restrictiile
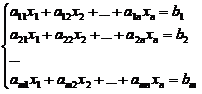
![]()
Problema definita mai sus este
|
a. |
de programare liniara in forma standard |
c. |
nici una din celelalte variante prezentate |
|
b. |
de programare liniara in forma canonica |
|
|
ANS: C
6.
Fie problema de programare liniara,
maximizeaza ![]()
cu restrictiile
![]()
![]()
![]()
Forma standard a problemei de mai sus este
|
a. |
maximizeaza cu restrictiile
|
c. |
maximizeaza cu restrictiile
|
|
b. |
minimizeaza cu restrictiile
|
d. |
maximizeaza cu restrictiile
|
ANS: A
7.
Fie problema de programare liniara,
maximizeaza ![]()
cu restrictiile
![]()
![]()
![]()
Forma standard a problemei de mai sus este
|
a. |
maximizeaza cu restrictiile
|
c. |
maximizeaza cu restrictiile
|
|
b. |
maximizeaza cu restrictiile
|
d. |
problema nu permite reprezentare in forma standard |
ANS: B
8.
Fie problema de programare liniara,
maximizeaza ![]()
cu restrictiile
![]()
![]()
![]()
![]()
Forma standard a problemei de mai sus este
|
a. |
maximizeaza cu restrictiile
|
c. |
maximizeaza cu restrictiile
|
||||
|
b. |
maximizeaza cu restrictiile
|
d. |
problema nu permite reprezentare in forma standard |
ANS: A
9.
Fie problema de programare liniara
maximimeaza ![]()
cu restrictiile
![]()
![]()
![]()
Forma matriceala este
Maximizeaza ![]()
cu restrictiile
![]()
![]()
![]() ,
,![]() R2
R2
Atunci matricea A este,
|
a. |
|
d. |
|
|
b. |
|
e. |
nici una din celelalte variante prezentate |
|
c. |
|
|
|
ANS: C
10.
Relatia
![]()
este echivalenta cu perechea de inegalitati
|
a. |
|
c. |
|
|
b. |
|
d. |
nici una din celelalte variante prezentate |
ANS: C
11. Daca o variabila xj nu este supusa
constrangerii de a fi nenegativa, xj poate fi inlocuita cu
perechea de variabile ![]() ,
unde
,
unde
|
a. |
|
c. |
|
|
b. |
|
d. |
nici una din celelalte variante prezentate |
ANS: A
12.
Fie problema de programare liniara,
maximizeaza![]()
cu restrictiile
![]()
![]()
![]()
Forma standard a problemei de mai sus este,
|
a. |
maximizeaza cu restrictiile
|
c. |
maximizeaza cu restrictiile
|
|
b. |
maximizeaza cu restrictiile
|
|
|
ANS: C
13. Fie restrictia![]() .
Pentru exprimarea acesteia in forma canonica, este considerata o variabila
suplimentara nenegativa,
.
Pentru exprimarea acesteia in forma canonica, este considerata o variabila
suplimentara nenegativa, ![]() ,
astfel incat
,
astfel incat
|
a. |
|
c. |
|
|
b. |
|
d. |
nici una din celelalte variante prezentate |
ANS: B
14.
In exprimarea matriceala, o
problema de programare liniara in forma canonica este descrisa astfel.
Determina vectorul ![]() Rn
care maximizeaza
Rn
care maximizeaza
![]()
cu restrictiile
![]()
![]()
Data A este
|
a. |
vector |
c. |
scalar |
|
b. |
matrice |
|
|
ANS: B
15.
In cazul unei probleme de programare liniara in forma canonica, cea de-a i-a restrictie este definita de,
![]() ,
pentru
,
pentru ![]()
sau, echivalent,
|
a. |
|
d. |
|
|
b. |
|
e. |
nici una din celelalte variante prezentate |
|
c. |
|
|
|
ANS: C
16.
Cea de-a i-a restrictie a problemei,
![]()
este exprimata in forma
vectoriala prin, pentru ![]()
|
a. |
|
c. |
|
|
b. |
|
d. |
nici una din celelalte variante prezentate |
ANS: A
17.
Fie ![]() solutii admisibile ale unei probleme de
programare liniara P. Elementele multimii,
solutii admisibile ale unei probleme de
programare liniara P. Elementele multimii,
![]()
sunt
|
a. |
solutii optimale ale lui P |
c. |
solutii oarecare ale lui P |
|
b. |
solutii admisibile ale lui P |
d. |
nici una din celelalte variante prezentate |
ANS: B
18.
Hiperplanul definit de ![]() ,
,
![]() ,
imparte Rn in doua semispatii inchise,
,
imparte Rn in doua semispatii inchise,
![]()
![]()
cu proprietatile
|
a. |
|
c. |
|
|
b. |
|
d. |
nici una din variantele de mai sus |
ANS: A
19. Multimea solutiilor admisibile ale unei probleme de programare liniara este multime
|
a. |
convexa |
c. |
concava |
|
b. |
nici una din celelalte variante prezentate |
d. |
finita |
ANS: A
20. Fie P o problema de programare liniara. Deoarece multimea solutiilor admisibile ale lui P, F, este intersectia tuturor hiperplanelor inchise definite de setul de restrictii ale lui P, rezulta ca F este
|
a. |
poliedru convex, daca nu este multimea vida |
c. |
poliedru concav, daca nu este multimea vida |
|
b. |
poliedru convex, daca este multimea vida |
d. |
poliedru concav, daca este multimea vida |
ANS: A
21. Multimea solutiilor unui sistem liniar de m ecuatii cu n necunoscute este
|
a. |
convexa |
c. |
concava |
|
b. |
finita |
d. |
nici una din celelalte variante prezentate |
ANS: A
22.
Un punct ![]() se numeste combinatie convexa a punctelor
se numeste combinatie convexa a punctelor ![]()
![]() daca
exista
daca
exista ![]() cu
cu
![]()
![]()
astfel incat
|
a. |
|
c. |
|
|
b. |
|
d. |
nici una din celelalte variante prezentate |
ANS: B
23. Multimea tuturor combinatiilor convexe definite pe un set finit de puncte din Rn este
|
a. |
concava |
c. |
nici una din celelalte variante prezentate |
|
b. |
vida |
|
|
ANS: C
24. Fie S o multime convexa in Rn.
Un element ![]() este
punct extrem daca si numai daca
este
punct extrem daca si numai daca
|
a. |
nu este combinatie convexa a nici unui subset al lui S care contine u |
d. |
este combinatie concava a unui subset unic al lui S care contine u |
|
b. |
este combinatie convexa a unui subset unic al lui S care nu contine u |
e. |
nici una din celelalte variante prezentate |
|
c. |
nu este combinatie convexa a nici unui subset al lui S care nu contine u |
|
|
ANS: C
25. Fie ![]() ;
restrictia
;
restrictia ![]() defineste semispatiul inchis
defineste semispatiul inchis
|
a. |
|
c. |
|
|
b. |
|
d. |
nici una din celelalte variante prezentate |
ANS: B
26. Primul pas al metodei simplex presupune
|
a. |
constructia functiei obiectiv |
c. |
determinarea unei solutii de baza admisibile initiale |
|
b. |
determinarea unei solutii de baza oarecare la momentul initial |
d. |
nici una din celelalte variante prezentate |
ANS: C
27. Cel de-al treilea pas al metodei simplex presupune
|
a. |
verificarea criteriului de optimalitate |
c. |
selectarea tabelului curent |
|
b. |
selectarea coloanei pivotale (variabila de intrare) |
d. |
nici una din celelalte variante prezentate |
ANS: B
28. Cel de-al patrulea pas al metodei simplex presupune
|
a. |
verificarea criteriului de optimalitate |
d. |
selectarea tabelului curent |
|
b. |
selectarea coloanei pivotale (variabila de intrare) |
e. |
nici una din celelalte variante prezentate |
|
c. |
selectarea liniei pivotale (variabila de iesire) |
|
|
ANS: C
29. La cel de-al patrulea pas al metodei simplex, daca nu
exista nici un ![]() raport
nenegativ si nenul, variabila de intrare poate creste oricat si problema de
programare liniara nu are solutie optima finita, caz in care algoritmul
raport
nenegativ si nenul, variabila de intrare poate creste oricat si problema de
programare liniara nu are solutie optima finita, caz in care algoritmul
|
a. |
se opreste |
c. |
continua |
|
b. |
cicleaza |
d. |
nici una din celelalte variante prezentate |
ANS: A
30. Cel de-al cincilea pas al metodei simplex presupune
|
a. |
verificarea criteriului de optimalitate |
d. |
constructia noului tabel |
|
b. |
selectarea coloanei pivotale (variabila de intrare) |
e. |
nici una din celelalte variante prezentate |
|
c. |
selectarea liniei pivotale (variabila de iesire) |
|
|
ANS: D
31.
Fie problema de programare liniara
maximizeaza ![]()
cu restrictiile,
![]()
Problema duala este,
|
a. |
minimizeaza cu restrictiile,
|
c. |
minimizeaza cu restrictiile,
|
|
b. |
maximizeaza cu restrictiile,
|
d. |
nici una din celelalte variante prezentate |
ANS: D
32.
Fie problema primala de programare liniara,
maximizeaza ![]()
cu restrictiile,
![]()
Pentru fiecare j, variabila
![]() este
este
|
a. |
cantitatea (necunoscuta) din cea de-a j-a iesire care trebuie produsa |
d. |
necesarul (cunoscut) din cea de-a j-a resursa care trebuie utilizata |
|
b. |
cantitatea (cunoscuta) din cea de-a j-a iesire care trebuie produsa |
e. |
nici una din celelalte variante prezentate |
|
c. |
necesarul (necunoscut) din cea de-a j-a resursa care trebuie utilizata |
|
|
ANS: A
33. Cea de-a i-a componenta a unei solutii optimale a problemei duale reprezinta
|
a. |
contributia adusa profitului de o unitate din cea de-a i-a iesire |
d. |
contributia adusa costului de o unitate din cea de-a i-a iesire |
|
b. |
contributia adusa profitului de o unitate din cea de-a i-a intrare |
e. |
nici una din celelalte variante prezentate |
|
c. |
contributia adusa costului de o unitate din cea de-a i-a intrare |
|
|
ANS: B
34. Criteriul de optim al metodei simplex poate fi reformulat astfel: tabelul simplex curent reprezinta o solutie optimala daca si numai daca
|
a. |
pentru orice |
d. |
exista |
|
b. |
exista |
e. |
nici una din celelalte variante prezentate |
|
c. |
pentru orice |
|
|
ANS: C
35.
Tentativa de rezolvare a unei probleme de programare liniara are urmatoarele rezultate alternative
1. Nu exista solutii admisibile
2. Exista o solutie optimala finita
3. Exista solutii admisibile, dar functia obiectiv este nemarginita.
|
a. |
1+2 |
d. |
1+2+3 |
|
b. |
1+3 |
e. |
2 |
|
c. |
2+3 |
|
|
ANS: D
36. Daca problema primala are solutii admisibile, dar functia obiectiv este nemarginita, atunci problema duala
|
a. |
nu are solutii fezabile |
c. |
are un numar impar de solutii fezabile |
|
b. |
are o solutie fezabila |
|
|
ANS: A
37.
Fie problema de optimizare neliniara,
Minimizeaza ![]()
cu restrictiile
![]()
unde ![]() constanta
(de obicei cu valoare foarte mare) si functia
constanta
(de obicei cu valoare foarte mare) si functia ![]() este definita prin,
este definita prin,
![]()
Ea este echivalenta cu
|
a. |
Minimizeaza
cu restrictiile
|
c. |
Minimizeaza
cu restrictiile
|
|
b. |
Maximizeaza
cu restrictiile
|
d. |
nici una din celelalte variante prezentate |
ANS: A
38. Consideram disponibil istoricul randamentelor
procentuale pe m perioade de timp pentru fiecare actiune dintr-un grup
de n actiuni si notam cu ![]() ,
randamentul actiunii i in perioada j;
,
randamentul actiunii i in perioada j; ![]() ,
fractiunea investita in actiunea i, astfel incat
,
fractiunea investita in actiunea i, astfel incat ![]() ;
;![]() ,
varianta actiunii i;
,
varianta actiunii i;![]() ,
covarianta dintre actiunile i si k. Portofoliul este definit de
fractiunile de investitii
,
covarianta dintre actiunile i si k. Portofoliul este definit de
fractiunile de investitii ![]() .
Randamentul mediu al fiecarei actiuni
.
Randamentul mediu al fiecarei actiuni ![]() ,
,
![]() ,
este calculat prin,
,
este calculat prin,
|
a. |
|
c. |
|
|
b. |
|
d. |
nici una din celelalte variante prezentate |
ANS: A
39. Problema standard a minimizarii riscului portofoliului
![]() ,
RISCMIN0, poate fi modificata prin eliminarea restrictiei si a variabilei
,
RISCMIN0, poate fi modificata prin eliminarea restrictiei si a variabilei ![]() ,
deoarece
,
deoarece
|
a. |
|
d. |
|
|
b. |
|
e. |
nici una din celelalte variante prezentate |
|
c. |
|
|
|
ANS: D
40.
Metoda secantei are la baza
interpolarea liniara; daca F' este evaluat in punctele ![]() ,
atunci
,
atunci
![]()
este o estimatie a punctului in care F'
|
a. |
se anuleaza |
c. |
este strict negativ |
|
b. |
este strict pozitiv |
d. |
nici una din celelalte variante |
ANS: A
41.
In tabelul urmator este prezentat istoricul randamentelor corespunzatoare actiunilor A1 si A2 pe primele 6 luni ale anului.
|
|
Ianuarie |
Februarie |
Martie |
Aprilie |
Mai |
Iunie |
|
A1 |
1.2 |
1.3 |
1.4 |
1.5 |
1.1 |
1.2 |
|
A2 |
1.3 |
1.0 |
0.8 |
0.9 |
1.4 |
1.3 |
Randamentul mediu al portofoliului este dat de vectorul
|
a. |
|
d. |
|
|
b. |
|
e. |
nici una din celelalte variante prezentate |
|
c. |
|
|
|
ANS: B
42. Pentru rezolvarea problemelor de optim, unele metode necesita si calculul derivatelor partiale de ordinul II, adica a matricei
|
a. |
Hessian |
c. |
nici una din celelalte variante |
|
b. |
Gradient |
|
|
ANS: A
43.
Fie setul de restrictii ale unei probleme de programare liniara,
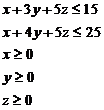
Un punct din cele listate mai jos nu apartine multimii solutiilor admisibile ale problemei.
|
a. |
|
c. |
|
|
b. |
|
d. |
|
ANS: B
44. Matricea simetrica A este pozitiv definita daca
si numai daca, pentru orice ![]() ,
are loc relatia
,
are loc relatia
|
a. |
|
c. |
|
|
b. |
|
d. |
|
ANS: A
45.
Fie problema primara de
minimizare a riscului in cazul unui portofoliu definit de fractiunile de
investitii ![]() ,
RISCMIN0,
,
RISCMIN0,
Minimizeaza ![]()
Problema RISCMIN0 poate fi rezolvata prin abordare analitica, astfel. Deoarece functia gradient este,
![]()
valoarea optimala a lui x este obtinuta prin rezolvarea sistemului liniar,
|
a. |
|
c. |
|
|
b. |
|
d. |
nici una din variantele celelalte |
ANS: A
NUMERIC RESPONSE
1.
Daca ![]() sunt
ultimile m coloane ale lui A (matrice cu n coloane) si
sunt liniar independente si daca
sunt
ultimile m coloane ale lui A (matrice cu n coloane) si
sunt liniar independente si daca
![]()
unde 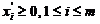 ,
atunci
,
atunci ![]() este punct extrem al lui S, unde
este punct extrem al lui S, unde ![]()
ANS:
0
2. Metodele gradient au avantajul ca permit definirea unui test de convergenta evident, si anume algoritmul este incheiat cand gradientul este apropiat de valoarea
ANS:
0
COMPLETION
1. O problema in care fie functia obiectiv, fie membrul drept al unei constrangeri sunt functii neliniare este problema de programare
ANS: neliniara
2. Orice restrictie de tip egalitate poate fi transformata intr-o pereche de .
ANS: inegalitati
3. Un vector ![]() Rn
care satisface restrictiiile problemei de programare liniara este numit solutie
fezabila sau . a problemei.
Rn
care satisface restrictiiile problemei de programare liniara este numit solutie
fezabila sau . a problemei.
ANS: admisibila
4. O solutie admisibila care optimizeaza functia obiectiv a unei probleme de programare liniara se numeste solutie .
ANS: optimala
5. Variabila suplimentara utilizata pentru exprimarea unei restrictii de tip inegalitate intr-o restrictie de tip egalitate se numeste variabila .
ANS: slack
6.
In cazul unei probleme de programare liniara in forma canonica, cea de-a i-a restrictie este definita de relatia
![]()
Multimea punctelor ![]() Rn
care satisfac relatia de mai sus este un .al lui Rn
Rn
care satisfac relatia de mai sus este un .al lui Rn
ANS: hiperplan
7. Pe baza definitiei solutiei admisibile a problemei de programare liniara, P, rezulta ca multimea solutiilor admisibile ale lui P este tuturor hiperplanelor inchise definite de setul de restrictii ale lui P.
ANS: intersectia
8. Un semispatiu inchis este multime
ANS: convexa
9.
O multime convexa se numeste daca este inclusa intr-un dreptunghi, adica o multime de tipul
![]()
unde ![]() ,
,
![]() R,
R,
![]() .
.
ANS: marginita
10.
Fie S o multime
convexa. Un punct ![]() se
numeste punct.. al lui S daca, pentru orice pereche de
puncte distincte
se
numeste punct.. al lui S daca, pentru orice pereche de
puncte distincte ![]() ,
,
![]()
ANS: extrem
11. Daca ![]() este punct extrem al lui S, atunci
coloanele matricei A care corespund componentelor strict pozitive ale
lui x formeaza un set de vectori liniar in Rm.
este punct extrem al lui S, atunci
coloanele matricei A care corespund componentelor strict pozitive ale
lui x formeaza un set de vectori liniar in Rm.
ANS: independenti
12. Fie S multimea solutiilor admisibile ale unei probleme de programare liniara P. Daca S este nevida si marginita, atunci exista o solutie optimala a problemei P si aceasta este punct . al lui S.
ANS: extrem
13.
Fie ![]() solutii admisibile ale unei probleme de
programare liniara P. Elementele multimii,
solutii admisibile ale unei probleme de
programare liniara P. Elementele multimii,
![]()
sunt .ale lui P.
ANS: solutii admisibile
14. Fie S multimea solutiilor admisibile ale unei probleme de programare liniara P. Daca P nu are solutie optimala, atunci S este fie vida, fie ..
ANS: nemarginita
15. Fie P problema de programare liniara in forma
canonica. P are un numar finit de solutii de baza si admisibile,
inferior lui ![]() ,
care reprezinta numarul solutiilor .. . ale lui P.
,
care reprezinta numarul solutiilor .. . ale lui P.
ANS: de baza
16. Fie P problema de programare liniara in forma standard, S multimea solutiilor admisibile ale lui P si S' multimea solutiilor admisibile ale variantei canonice ale lui P. Orice punct extrem al lui S determina obtinerea unui punct extrem al lui S' prin adaugarea variabilelor Reciproc, orice punct extrem al lui S' determina, prin trunchiere, obtinerea unui punct extrem al lui S.
ANS: slack
17. Multimea convexa a solutiilor admisibile ale unei probleme de programare liniara in forma standard are un numar de puncte extreme.
ANS: finit
18. Fie S multimea solutiilor admisibile ale problemei de programare liniara definita in forma standard. Doua puncte extrem ale lui S sunt daca au in comun, ca solutii de baza si admisibile, una si numai una din variabilele de baza considerate.
ANS: adiacente
19. Criteriul de oprire pentru metoda simplex este urmatorul. Daca linia obiectiv a tabelului contine in pozitiile variabilelor non-baza elemente, atunci este obtinut maximul functiei obiectiv si calculul se incheie.
ANS:
nenegative
pozitive
20. Se numeste solutie o solutie in care cel putin o variabila de baza este nula.
ANS: degenerata
21. La cel de-al patrulea pas al metodei simplex,
cresterea variabilei de intrare este data de rapoartele dinte elementele de pe
coloana cea mai din dreapta (solutia admisibila de baza de la momentul curent)
si valorile corespunzatoare de pe coloana., numite ![]() rapoarte.
rapoarte.
ANS: pivotala
22. La cel de-al cincilea pas al metodei simplex este construit tabelul rezultat in urma modificarii setului solutiilor de baza admisibile prin stabilirea variabilelor de intrare si de iesire. Procedura este numita de
ANS: pivotare
23.
Fie perechea de probleme de programare liniara,
(1) maximizeaza ![]()
cu restrictiile,
![]()
si
(2) minimizeaza ![]()
cu restrictiile,
![]()
unde ![]() este o matrice
este o matrice ![]() ,
,
![]() sunt vectori cu n componente si
sunt vectori cu n componente si ![]() sunt
vectori cu m componente. Problemele (1) si (2) se numesc ..
sunt
vectori cu m componente. Problemele (1) si (2) se numesc ..
ANS: duale
24.
Fie perechea de probleme de programare liniara,
(1) maximizeaza ![]()
cu restrictiile,
![]()
si
(2) minimizeaza ![]()
cu restrictiile,
![]()
unde ![]() este o matrice
este o matrice ![]() ,
,
![]() sunt vectori cu n componente si
sunt vectori cu n componente si ![]() sunt
vectori cu m componente. Problema (1) se numeste problema..,
iar problema data prin (2) se numeste problema
sunt
vectori cu m componente. Problema (1) se numeste problema..,
iar problema data prin (2) se numeste problema
ANS: primala duala
25.
Fie problema de programare liniara in forma canonica,
maximizeaza ![]()
cu restrictiile,
![]()
Forma duala este problema de programare liniara,
minimizeaza ![]()
cu restrictiile,
![]()
w
ANS:
nerestrictionat
neconstrans
26.
Fie problema primala de programare liniara,
maximizeaza ![]()
cu restrictiile,
![]()
Pentru fiecare i si j,
coeficientul ![]() reprezinta cantitatea din cea de-a -a intrare
necesara unei unitati din cel de-al .-lea produs
reprezinta cantitatea din cea de-a -a intrare
necesara unei unitati din cel de-al .-lea produs
ANS: i j
27.
Fie problema primala de programare liniara,
maximizeaza ![]()
cu restrictiile,
![]()
Coeficientul ![]() din
functia obiectiv reprezinta sau valoarea derivata in urma producerii
unei unitati din cea de-a j-a iesire.
din
functia obiectiv reprezinta sau valoarea derivata in urma producerii
unei unitati din cea de-a j-a iesire.
ANS:
profitul
profit
28.
Fie perechea de probleme de programare liniara primala, respectiv duala,
(1) maximizeaza ![]()
cu restrictiile,
![]()
si
(2) minimizeaza ![]()
cu restrictiile,
![]()
In cazul unei solutii
optimale a problemei primale, profitul, egal cu ![]() ,
este dat si prin
,
este dat si prin ![]() ,
pe baza teoremei ..
,
pe baza teoremei ..
ANS: dualitatii
29. In problema duala sunt cautate preturile ascunse ale fiecarei resurse (intrari) care sa .pretul lor total, cu constrangerea ca aceste preturi sa determine obtinerea unor valori corespunzatoare pentru fiecare unitate de iesire produsa mai mari sau egale cu profiturile fiecarei unitati de produs.
ANS: minimizeze
30. Daca problema duala are solutii fezabile, dar functia obiectiv este., atunci problema primala nu are solutii admisibile.
ANS: nemarginita
31. In unele situatii, restrictiile de tip pot fi utilizate pentru eliminarea variabilelor unei probleme de optimizare.
ANS: egalitate
32. Consideram disponibil istoricul randamentelor
procentuale pe m perioade de timp pentru fiecare actiune dintr-un grup
de n actiuni si notam cu ![]() ,
randamentul actiunii i in perioada j;
,
randamentul actiunii i in perioada j; ![]() ,
fractiunea investita in actiunea i, astfel incat
,
fractiunea investita in actiunea i, astfel incat ![]() ;
;![]() ,
varianta actiunii i;
,
varianta actiunii i;![]() ,
covarianta dintre actiunile i si k. Portofoliul este definit de
fractiunile de investitii
,
covarianta dintre actiunile i si k. Portofoliul este definit de
fractiunile de investitii ![]() .Varianta
portofoliului este definita prin
.Varianta
portofoliului este definita prin ![]() si
este utilizata ca masura a .. portofoliului.
si
este utilizata ca masura a .. portofoliului.
ANS: riscului
33.
In general, un portofoliu este considerat optim daca el furnizeaza cel mai mare randament cu cel mai mic
ANS: risc
34. Optimizarea prin metode . utilizeaza derivatele
functiei obiectiv si rezolva iterativ ecuatia neliniara ![]() .
.
ANS: gradient
35. Metoda .. determina minimul unei functii F(x) prin utilizarea primelor doua derivate ale functiei F.
ANS: Newton
36.
Procedura MINRISC0
defineste problema primara de a riscului in cazul unui
portofoliu definit de fractiunile de investitii ![]() .
.
MINRISC0:
Minimizeaza ![]()
ANS: minimizare
37.
Functia obiectiv a unei
probleme de programare liniara este ![]() .
Fie k o constanta. Graficul ecuatiei
.
Fie k o constanta. Graficul ecuatiei ![]() este
un hiperplan. In ipoteza in care problema de optim este una de maxim, trebuie
determinate acele puncte
este
un hiperplan. In ipoteza in care problema de optim este una de maxim, trebuie
determinate acele puncte ![]() Rn
din multimea solutiilor admisibile pentru care valoarea lui k este cea
mai mare posibila. Din punct de vedere geometric, acest lucru revine la
determinarea unui hiperplan care intersecteaza multimea solutiilor admisibile
si pentru care k este
Rn
din multimea solutiilor admisibile pentru care valoarea lui k este cea
mai mare posibila. Din punct de vedere geometric, acest lucru revine la
determinarea unui hiperplan care intersecteaza multimea solutiilor admisibile
si pentru care k este
ANS: maxim
38.
In general, in problemele de optimizare a portofoliilor, vectorul gradient si matricea Hessian pot fi calculate direct, functiile obiectiv fiind in general . diferentiabile.
ANS: dublu
39.
Fie ![]() functie de n variabile, continua si
diferentiabila. Caracterizarea punctului de minim atins de F este realizata in
termenii vectorului .. si a matricei Hessian
functie de n variabile, continua si
diferentiabila. Caracterizarea punctului de minim atins de F este realizata in
termenii vectorului .. si a matricei Hessian
ANS: gradient
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2026 - Toate drepturile rezervate -| |
|
|
|||
|
|||
|
|||
Lucrari pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||