
| Biologie | Botanica | Chimie | Didactica | Fizica | Geografie |
| Gradinita | Literatura | Matematica |
Matematica
|
|
Qdidactic » didactica & scoala » matematica Metode numerice pentru rezolvarea sistemelor de ecuatii algebrice liniare |
Metode numerice pentru rezolvarea sistemelor de ecuatii algebrice liniare
METODE NUMERICE PENTRU REZOLVAREA SISTEMELOR DE ECUATII ALGEBRICE LINIARE.
Metode de rezolvare numerica a sistemelor algebrice liniare
Modelarea numerica a proceselor tehnologice de multe ori duce la obtinerea unor sisteme de ecuatii liniare. Procedeul Kramer, care permite obtinerea solutiei sistemului prin raportul determinatilor, devine inutil daca numarul de ecuatii si necunoscute creste
( n >10 ), deoarece numarul necesar de operatii aritmetice are o valoare fantastica n!n.
In acest caz rezolvare sistemelor liniare se face folosind anumite metode specifice, care pot fi clasificate ca:
metode directe ;
- metode indirecte (sau iterative).
Metodele directe se utilizeaza pentru rezolvarea sistemelor liniare de ordinul n < 103. Metodele indirecte se utilizeaza pentru rezolvarea sistemelor liniare de pana la ordinul n = 106.
NOTA. Ca regula , pentru rezolvarea sistemelor de ecuatii liniare, se aplica metode iterative.
1.1. Metoda eliminarii Gauss
Metoda eliminarii Gauss este cea mai simpla metoda directa, care cere circa (2/3)·n3 de operatii aritmetice. Metoda are la baza ideea transformarii matricei date A intr-o matrice superior triunghiulara prin eliminarea consecutiva a necunoscutelor si apoi rezolvarea ecuatiilor, folosind procedeul de substituire inversa .
Descrierea metodei
Se considera un sistem de n ecuatii liniare, de forma:
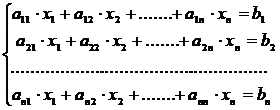 (1)
(1)
care scris mai scurt va avea forma
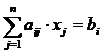 , (2)
, (2)
unde :
i = 1,2,3,.., n este numarul ecuatiei;
j = 1,2,3, , n reprezinta numarul necunoscutei
Acest sistem in forma matriceala se noteaza:
A·x = b , (3)
la care:
A 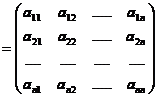 se numeste matricea coeficientilor ,
se numeste matricea coeficientilor ,
x ![]() - vectorul variabilelor necunoscute,
- vectorul variabilelor necunoscute,
b ![]() - vectorul termenelor
liberi.
- vectorul termenelor
liberi.
![]() Daca matricea A
este superior triunghiulara, adica
toate elementele situate sub diagonala principala sunt nule :
Daca matricea A
este superior triunghiulara, adica
toate elementele situate sub diagonala principala sunt nule :

(coeficientii aij = 0, la i > j), atunci rezolvarea sistemului se poate face usor prin procedeul de eliminare inversa.
Daca toate elemente din matricea superior triunghiulara A de pe diagonala principala sunt diferite de zero (aii 0) atunci sistemul de ecuatii dat ( 1) va capata forma :
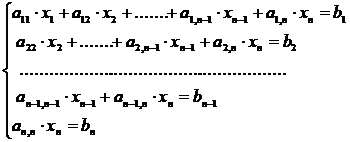 (4)
(4)
Se observa ca ultima ecuatie contine numai necunoscuta xn, atunci considerand
an,n 0 , se obtine
xn = bn/an,n (5)
Substituind aceasta valoare in penultima ecuatie rezulta ecuatia :
an-1,n-1 xn- + an-1,n bn /ann = bn- (6)
din care vom avea necunoscuta xn-1 ( avand in vedere ca an-1,n-1
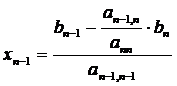 (7)
(7)
Introducand valorile cunoscute pentru xn si xn-1 in ecuatia imediat anterioara rezulta necunoscuta xn- Daca procedura se repeta pana la prima ecuatia va rezulta prima necunoscuta x1.
Problema care nu a fost deocamdata clarificata este de a gasi procedeul prin care un sistem de ecuatii liniare structurat arbitrar sa fie transformat intr-o forma cu matricea superior triunghiulara, pentru putea aplica procedeul de substituire inversa examinat anterior.
Se considera un
sistem cu n ecuatii liniare (1)
scris in forma (2). Notand
termeni liberi ![]() se obtine:
se obtine:
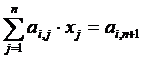 , (8) la care i
= 1,2,3,.., n este numarul ecuatiei; j = 1,2,3, , n reprezinta numarul
necunoscutei.
, (8) la care i
= 1,2,3,.., n este numarul ecuatiei; j = 1,2,3, , n reprezinta numarul
necunoscutei.
Presupunem, ca in prima ecuatie
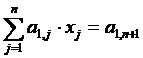 (9)
(9)
primul coeficient a11 ≠ 0 (in cazul
contrar se face renumerarea necunoscutelor). Eliminam din aceasta
ecuatie coeficientul din fata primei necunoscute x1 impartind-o
cu a11
. Notand 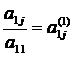 , iar
, iar 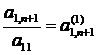 se obtine:
se obtine:
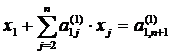 , (10)
, (10)
Multiplicand ecuatia (10) consecutiv cu ai1, unde i=2,,n , si scazand-o din ecuatia i se elimina prima variabila x1 din toate ecuatiile sistemului (8) in afara de prima ecuatie. Atunci aceste ecuatii vor capata forma :
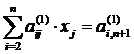 , i= 2,3,
., n (11)
, i= 2,3,
., n (11)
unde :
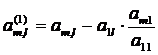 , m=2,3,.,n si l=2,3,., n+1 (12) La fel se procedeaza cu sistemul obtinut (11).
, m=2,3,.,n si l=2,3,., n+1 (12) La fel se procedeaza cu sistemul obtinut (11).
|
Dupa eliminarea necunoscutei xk-1, restul ecuatiilor va forma sistemul :
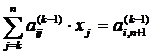 , (13) unde: i=
k , k+1,,n; j=i+1.
, (13) unde: i=
k , k+1,,n; j=i+1.
Eliminand elemente ale coloanei k, se obtine sistemul de ecuatii cu coeficientii :
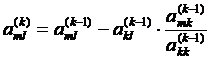 m=k+1,,n ; l=k+1,,n+1 (14)
m=k+1,,n ; l=k+1,,n+1 (14)
Eliminarea necunoscutelor duce la sistemul (4) cu matricea superior triunghiulara, care scris mai scurt are forma :
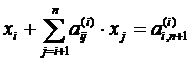 , (15)
, (15)
unde: i=1,2,, n.
Cu aceasta se incheie eliminarea Gauss si dupa aceasta, pentru determinarea necunoscutelor se aplica eliminarea inversa. Pentru aceasta se utilizeaza formula (15) transcrisa in forma (16), considerand i= n, n-1, n-2, , 2, 1 :
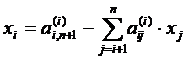 (16)
(16)
NOTA. Eliminarea Gauss prevede divizarea ecuatiilor pe elemente diagonale. Daca un coeficient diagonal este nul sau foarte mic dupa valoarea lui absoluta, eroarea de calcul
devine inadmisibil de mare. De aceea, inainte de aplicarea eliminarii, sistemul trebuie rearanjat astfel incat elementele diagonale sa fie dominante in valoarea absoluta.
Aplicatia 1. Exemplu de folosirea eliminarii gaussiene si a eliminarei inverse
Se considera ca analiza poceselui de amestecare a trei substante fluide cu trei concentratii volumice diferite a condus la urmatorul sistem de ecuatii :
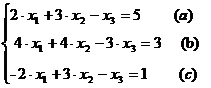
Se cere deteminarea concentratiilor volumice initiale x1, x2 si x3 .
Rezolvare
Sa notam coeficientii : a11 =2, a12 =3, a13 =-1, a21 =4, a22 =4 , a23 =-3, a31 =-2, a32 =3, a33 =-1 si termenii liberi cu b1=5 , b2= 3 , b3=1.
1. Ca sa eliminam pe x1 din ecuatia (b), inmultim ecuatia (a) cu coeficientul
- a21/a11 = - 42 si adunam rezultatul la ecuatia (b).
Se obtine ecuatia :
-2·x2 - x3 = -7 (b')
De asemenea, inmultim ecuatia (a) cu multiplicatorul -a31/a11= -(-22) si rezultatul obtinut se aduna la ecuatia (c).
Se obtine o noua ecuatie :
6·x2 - 2·x3 = 6 (c')
3. Acum se va elimina necunoscuta x2 din ecuatia (c'). Pentru aceasta, se inmulteste ecuatia (b') cu multiplicatorul -6(-2) si rezultatul obtinut se aduna la ecuatia (c') .
Rezulta :
- 5![]() = - 15 (c')
= - 15 (c')
Cu aceasta, noul sistem de ecuatii devine superior triunghiular :
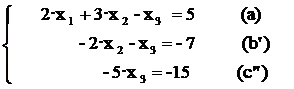 ,
,
sau in forma generalizata :
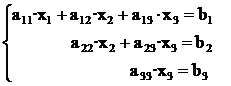
Rezolvarea sistemului transformat se face folosind procedeul de eliminare inversa :
x = b2 /a22 =
x = (b2 - a23·x3) /a22
x = (b1 - a12·x2 - a13·x3 )/a11
1. Metoda iteratiilor simple Iacobi
Se considera un sistem cu n ecuatii liniare :
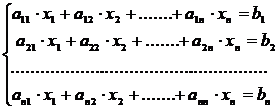
Considerand ca sistemul examinat este astfel structurat incat elementele diagonale
ai,i ( i=1,2,,n) sunt dominante in valoarea absoluta, rearanjam sistemul eliminand variabile xi din termeni care contin coeficientii aii de la fiecare rand in felul urmator :
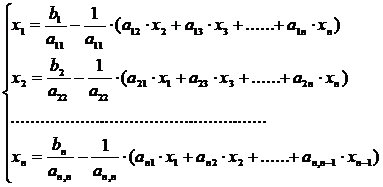 (17)
(17)
Daca in partea dreapta a sistemului (17) se introduce o solutie initiala xi(0 (care de cele mai multe ori se ia egala cu zero xi(0)=0 ), prin rezolvarea sistemului (17) se obtine prima solutie aproximativa xi(1) . Introducand noua solutie obtinuta in partea dreapta a sistemului se obtine a doua solutie aproximativa xi(2).
Continuand acest proces penrtu pasul k+1 se obtine solutia :
![]()
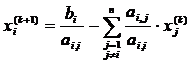 , (18)
, (18)
unde i = 1,2, ...,n ; j = 1,2, ...,n ![]()
O conditie suficienta pentru convergenta procesului iterativ este ca :
![]()
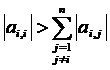 , (19) NOTA. Daca
conditie de convergenta este
satisfacuta, atunci si solutia cautata va converge
spre solutia reala, indiferent de valoarea aproximatiei
initiale x0.
, (19) NOTA. Daca
conditie de convergenta este
satisfacuta, atunci si solutia cautata va converge
spre solutia reala, indiferent de valoarea aproximatiei
initiale x0.![]()
Aplicatia Utilizarea metodei Iacobi (iteratiilor simple)
Se considera sistemul de ecuatii liniare :
![]()
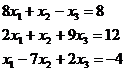
Se cere rezolvarea lui cu precizia ε =10-4 .
Rezolvare
Rearanjam ecuatiile in asa fel incat fiecare necunoscuta sa aiba cel mai mare coeficient :
![]()
![]()
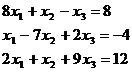
Rezolvam fiecare ecuatie fata de necunoscuta respectiva :
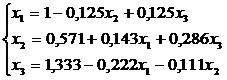
![]()
Alegem ca o
solutie initiala : ![]()
Rezulta prima solutie aproximativa:
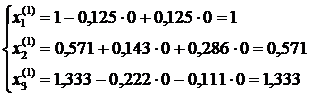
Introducem valorile obtinute
pentru ![]() in partea dreapta a
sistemului, rezultand o noua solutie :
in partea dreapta a
sistemului, rezultand o noua solutie :
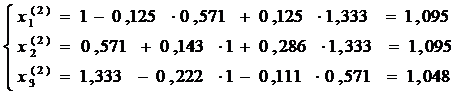
Dupam inlocuirea ![]() in partea
dreapta a sistemului , rezulta o noua solutie, etc.
in partea
dreapta a sistemului , rezulta o noua solutie, etc.
Din valorile numerice putem alcatuiun tabel :
Tabelul 1
|
Solutii |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
Din tabelul se vede ca dupa a 7S iteratia solutii nu se mai schimba.
Raspuns: ![]()
1.3. Metoda iterativa Gauss - Seidel
In acest caz, trecerea sistemului de ecuatii (17) de la iteratia (k) spre (k+1) nu se mai face simultan pentru toate ecuatiile,ci prin utiizarea solutiilor obtinute din ecuatii precedente. Pentru sistemul examinat iteratia (k+1) se realizeaza prin relatia:
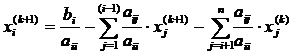 (19)
(19)
NOTA. Avantajul esential al acestei metode il constituie cresterea vitezei de convergenta, datorita reducerii numarului total de iteratii necesare.
Aplicatia 3. Utilizarea metodei iterative Gauss-Seidel.
Vom rezolva acelasi sistem din Aplicatia 2 , pentru a arata rapiditatea convergentei solutiei numerice la utilizarea metodei Gauss-Seidel. Deci , avem :
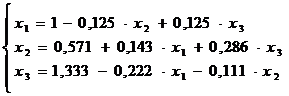
Rezolvare
Considerand solutia initiala ![]() in prima
ecuatie si se obtine
solutia
in prima
ecuatie si se obtine
solutia ![]() :
:
![]()
Dupa aceasta se rezolva a doua
ecuatie introducand ![]() si
si ![]()
![]() :
:
![]()
Considerand noile solutii:![]() si
si ![]() , se rezolva a treia ecuatia:
, se rezolva a treia ecuatia:
![]()
A doua iteratie se incepe prin introducerea solutiilor ![]() si
si ![]() in prima ecuatie , rezulta :
in prima ecuatie , rezulta :
![]()
Introducand ![]() si
si ![]() rezulta :
rezulta :
![]()
In fine, cu noi solutii ![]() si
si ![]() se obtine :
se obtine :
![]()
Procedand in mod asemanator se obtin rezultatele prezentate mai jos in tabelul 2 :
Tabelul 2
|
Solutia |
Numar de iteratii |
|||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
Din tabelul se vede ca dupa a 5- a iteratie solutii nu se mai schimba.
Raspuns: ![]()
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||
|
|||
|
|||
Referate pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








