
| Biologie | Botanica | Chimie | Didactica | Fizica | Geografie |
| Gradinita | Literatura | Matematica |
Statistica
|
|
Qdidactic » didactica & scoala » matematica » statistica Marimi medii de pozitie (mediana si modulul) - media in cazul caracteristicii alternative |
Marimi medii de pozitie (mediana si modulul) - media in cazul caracteristicii alternative
Marimi medii de pozitie (mediana si modulul) - Media in cazul caracteristicii alternative
Daca se considera necesar, pentru aprecierea nivelului mediu al unei caracteristici statistice se poate folosi, mediana sau modulul, ca valori tipice de pozitie, deoarece acestea ocupa un anumit loc cu semnificatie medie in cadrul unei serii de valori.
Mediana (XMe) este varianta caracteristicii care ocupa locul central in seria de date statistice care au fost ordonate crescator sau descrescator.
Pozitia ocupata de mediana in cadrul unei serii de repartitie prezentata ca o insiruire de variante se calculeaza asfel:
- locul
medianei: ![]()
Daca seria are un numar impar de valori, XMe, va fi varianta centrala localizata prin calculul locului medianei (Me).
Daca seria are un numar par de valori, XMe, va fi rezultatul mediei aritmetice simple efectuata din cele doua variante centrale.
In cazul seriilor de repartitie in care datele statistice sunt prezentate sub forma unor grupari pe intervale de grupare, calculul valorii mediane se realizeaza pe baza formulei:
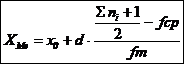
in care,
![]() este limita inferioara a intervalului
median,
este limita inferioara a intervalului
median,
d este marimea intervalului median, obtinuta ca diferenta intre limita superioara si limita inferioara a intervalului median,
![]() este locul sau, numarul de ordine pe care
il ocupa valoarea mediana si pe baza caruia se
stabileste intervalul median,
este locul sau, numarul de ordine pe care
il ocupa valoarea mediana si pe baza caruia se
stabileste intervalul median,
fcp este suma frecventelor tuturor intervalelor precedente, constituite pana la intervalul in care se gaseste valoarea mediana,
fm este frecventa intervalului in care se pozitioneaza valoarea mediana.
Quartilele sunt acele valori ale caracteristicii statistice care impart o serie de repartitie in patru zone egale, din punct de vedere al numarului unitatilor care formeaza o colectivitate. Aceasta procedura este folosita atunci cand numarul unitatilor statistice este suficient de mare si se considera necesar sa se constituie patru grupe egale care sa se caracterizeze printr-un anumit grad de omogenitate. Calculul quartilelor se bazeaza pe aceeasi logica metodologica folosita la calculul medianei, dar tinand seama de locul ocupat de quartila respectiva. Quartila 2 (Q2) este identica cu valoarea mediana iar quartila 1 (Q1) si respectiv quartila 3 (Q3) se calculeaza astfel:
|
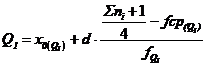
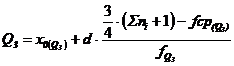
Decilele. In unele cazuri, in procesul de prelucrare al datelor statistice, se opteaza pentru calculul decilelor care sunt valori ale caracteristicii ce impart seria statistica in zece parti egale. Decila a cincea este egala cu valoarea mediana, iar calculul celorlalte decile tine seama de pozitia acesteia in cadrul seriei de valori ale caracteristicii. Decilele se calculeaza, de regula cand amplitudinea variatiei este mai mare, astfel:
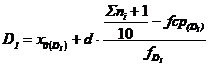
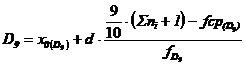
Modulul (XMo) reprezinta acea varianta a caracteristicii care are cea mai mare frecventa, sau, cu alte cuvinte, varianta care este inregistrata de cele mai multe unitati ale colectivitatii statistice.
Daca dispunem de o serie de repartitie in care datele statistice sunt prezentate sub forma unei grupari pe intervale de grupare, calculul valorii modale se realizeaza pe baza formulei:
![]()
in care,
![]() este limita inferioara a intervalului
modal. Intervalul modal este intervalul care are frecventa cea mai mare,
este limita inferioara a intervalului
modal. Intervalul modal este intervalul care are frecventa cea mai mare,
d este marimea intervalului modal, obtinuta ca diferenta intre limita superioara si limita inferioara a intervalului modal,
![]() este diferenta dintre frecventa intervalului
modal si frecventa intervalului precedent,
este diferenta dintre frecventa intervalului
modal si frecventa intervalului precedent,
![]() este diferenta dintre frecventa
intervalului modal si frecventa intervalului urmator.
este diferenta dintre frecventa
intervalului modal si frecventa intervalului urmator.
Sunt si cazuri in care frecvente maxime identice se inregistreaza la doua sau mai multe intervale de grupare sau la mai multe variante ale caracteristicii, in aceste situatii seriile de repartitie sunt denumite bimodale sau multimodale.
Exemplul 5.
Daca folosim datele statistice utilizate la exemplul 1, valoarea mediana si respectiv valoarea modala se calculeaza astfel:
|
Grupe de apartamente dupa consumul |
Numarul apartamentelor |
Marimea intervalului (lim. sup. lim. inf.) |
Frecventele |
|
6,0 6,5 |
5 |
0,5 |
5 |
|
6,5 7,0 |
7 |
0,5 |
12 |
|
7,0 7,5 |
10 |
0,5 |
22 |
|
7,5 8,0 |
6 |
0,5 |
28 |
|
8,0 8,5 |
2 |
0,5 |
30 |
|
Total |
30 |
|
|
Locul valorii mediane:
![]() ,
prin urmare mediana este valoarea medie a variantelor cu numarul de ordine
15 si 16 care se pozitioneaza in intervalul, 7,0 - 7,5
(intervalul median).
,
prin urmare mediana este valoarea medie a variantelor cu numarul de ordine
15 si 16 care se pozitioneaza in intervalul, 7,0 - 7,5
(intervalul median).
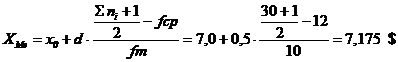
Intervalul modal este intervalul, 7,0 7,5 la care se inregistreaza frecventa maxima (10).
![]()
Media in cazul caracteristicii alternative
Programul observarii statistice poate cuprinde si caracteristici alternative, pentru care exista doua variante de raspuns exprimate prin da sau nu. Pentru a calcula nivelul mediu al unei astfel de caracteristici se inlocuiesc cu cifra 1 raspunsurile da (cand la o unitate statistica este caracteristica cercetata) si cu 0 raspunsurile nu (cand unitatea statistica nu detine caracteristica cercetata). Valoarea medie se determina cu ajutorul mediei aritmetice ponderate, astfel:
![]()
in care,
n1 este numarul de unitati care detin caracteristica studiata,
n2 este numarul de unitati care nu detin caracteristica studiata.
Prin urmare, valoarea medie a unei caracteristici alternative este egala cu proportia unitatilor statistice care detin caracteristica cercetata in totalul unitatilor care formeaza colectivitatea statistica.
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
 |
|||
|
|||
|
|||
Referate pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








