
| Biologie | Botanica | Chimie | Didactica | Fizica | Geografie |
| Gradinita | Literatura | Matematica |
Matematica
|
|
Qdidactic » didactica & scoala » matematica Extremele functiilor reale de mai multe variabile reale |
Extremele functiilor reale de mai multe variabile reale
Extremele functiilor reale de mai multe variabile reale
Multe dintre problemele care apar in practica sunt legate de determinarea valorilor extreme ale unei functii reala ce depinde de mai multe variabile. De exemplu, o functie poate reprezenta volumul productiei, care depinde de mai multe variabile reale este bine sa cunoastem pentru ce valori ale variabilelor volumul productiei este maxim.Valorile maxime sau minime ale unei functii se numesc extremele functiei. Am definit mai sus, notiunea de punct de minim si respectiv maxim local.
Fie f:D R2 R si x0=(a,b)ID.
Teorema (Conditiile necesare pentru existenta unui extrem)
Daca functia f admite derivate partiale de ordinul intai intr-o vecinatate a punctului x0 si x0 este punct de extrem local pentru functia f, atunci derivatele partiale ale lui f sunt nule in acest punct, adica:
![]() ,
, ![]() .
.
Punctele
determinate de solutiile reale ale sistemului de ecuatii ![]() ,
, ![]() se numesc puncte
critice sau stationare.
se numesc puncte
critice sau stationare.
Teorema ( Conditia suficienta de extrem)
Functia f: D R2 R, care admite derivate partiale de ordinul al doilea pe D, are un punct de extrem local in punctul stationar (a,b)ID, daca:
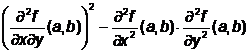 < 0.
< 0.
Punctul (a,b) este punct de
maxim local daca ![]() < 0 si este punct de minim
local al functiei f daca
< 0 si este punct de minim
local al functiei f daca ![]() > 0.
> 0.
Notam
cu a11=![]() , a12=
, a12=![]() si a22
si a22![]() si putem scrie Hessiana lui f in acest punct Hf(x0)
si putem scrie Hessiana lui f in acest punct Hf(x0)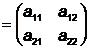 .
.
Rezulta ca
punctul stationar (a,b) este punct de minim local pentru f daca
determinantii D1 a11 > 0 si D2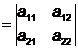 >0 si
>0 si
|
este punct de maxim local daca D1< 0 si D2>0.
Exemplu. Sa se determine punctele de extrem local ale functiei
f(x,y)=3x3+y2-9x2-27x+2.
Vom determina mai intai punctele stationare ale lui f, rezolvand sistemul de ecuatii
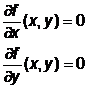
![]() .
.
Exista doua puncte stationare M1(-1,0) si M2(3,0). Pentru a vedea care dintre ele este punct de extrem local pentru f, va trebui sa calculam derivatele de ordinul al doilea ale lui f.
![]() ;
; ![]() ;
; ![]() care sunt functii continue pe R2.
care sunt functii continue pe R2.
In punctul M1(-1,0) : 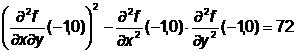 >0, deci nu este extrem.
>0, deci nu este extrem.
In punctul
M2(3,0):  -72<0 si
-72<0 si ![]() =36>0, deci M2
este punct de minim local al functiei f. Valoarea minima a
functiei f este f(3,0)= -79.
=36>0, deci M2
este punct de minim local al functiei f. Valoarea minima a
functiei f este f(3,0)= -79.
Fie functia f:D Rn R de n variabile reale, n>2.
Un punct stationar pentru functia f este o solutie a sistemului de n ecuatii cu n necunoscute:
![]()
![]()
![]()
Vom considera a=(a1,a2,.,an)IA un punct stationar al lui f. Presupunem ca f admite derivate
partiale de ordinul doi continue intr-o vecinatate a acestui punct
si le
vom nota cu aij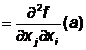 , i,j
, i,j![]() .
.
Hessiana lui f in punctul a este matricea H=(aij)![]() , ale carei elemente sunt definite mai sus. Notam
determinantii principali ai matricei H cu
, ale carei elemente sunt definite mai sus. Notam
determinantii principali ai matricei H cu ![]() ;
;
D1 a11 si D2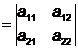 Dn=det H.
Dn=det H.
Daca D1>0, D2>0,., Dn>0 atunci a este un punct de minim local pentru functia f
daca D1<0, D2>0, D3<0..( semnele alterneaza incepand cu minus), atunci a este punct de maxim local. In celelalte cazuri punctele stationare nu sunt puncte de extrem.
Metoda aceasta de studiu a punctelor de extrem local ale unei functii reale de mai multe variabile reale consta in calculul diferentialei de ordinul al doilea a functiei in fiecare punct critic si daca este o forma patratica pozitiv definita atunci punctul critic studiat este minim local ; iar daca este negativ definita atunci este maxim local al functiei respective.
Probleme propuse
1.Fie functia f:D R2 R, f(x,y)=arctg![]() .Sa se calculeze derivatele partiale de ordinul
intai si doi si df(-1,2), df(-1,2)(3,-2); d2f(-1,2);d2f(-1,2)(3,-2).
.Sa se calculeze derivatele partiale de ordinul
intai si doi si df(-1,2), df(-1,2)(3,-2); d2f(-1,2);d2f(-1,2)(3,-2).
2.Sa se calculeze derivatele partiale de ordinul intai si doi ale functiilor:
a)
f(x,y)=xy+![]() , definita pe multimea A=;
, definita pe multimea A=;
b)
f(x,y)= , definita pe multimea A=R2;
, definita pe multimea A=R2;
c)
f(x,y,z)=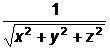 , definita pe multimea A=R3;
, definita pe multimea A=R3;
d)
f(x,y)=arctg![]() , definita pe multimea A=;
, definita pe multimea A=;
e) f(x,y)=ln (x+y2), definita pe multimea A=;
f)
f(x,y,z)=![]() +zln(x+y), definita pe multimea A=.
+zln(x+y), definita pe multimea A=.
3. Sa se afle extremele functiilor: f:D R
a) f(x,y)=xy2ex-y ;
b) f(x,y)=xy(x+y-3) ;
c)
f(x,y)=xy+![]() ;
;
d) f(x,y)=xy ln(x2+y2) ;
e) f(x,y,z)=x3+y2+z2+12xy+2z ;
f)
f(x,y,z)=x+![]() .
.
4. Folosind formula lui Taylor pentru functia f:D R2 R f(x,y)=xy
in jurul punctului (1,1) sa se aproximeze printr-un numar cu 3 zecimale.
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||
|
|||
|
|||
Analize pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








