
| Afaceri | Agricultura | Comunicare | Constructii | Contabilitate | Contracte |
| Economie | Finante | Management | Marketing | Transporturi |
Management
|
|
Qdidactic » bani & cariera » management Conducerea unui cu ajutorul metodelor planificarii in retea |
Conducerea unui cu ajutorul metodelor planificarii in retea
CONDUCEREA UNUI PROIECT CU AJUTORUL METODELOR PLANIFICARII IN RETEA
1. Generalitati
Un proiect este constituit dintr-un numar de activitati. O activitate este o parte a proiectului si are urmatoarele proprietati:
- are un punct de inceput si unul de sfarsit care se pot identifica in mod cert, denumite evenimente;
- are o durata, care este timpul scurs intre evenimentul de inceput si cel de sfarsit al activitatii;
- consuma resurse.
Pentru analiza, programarea activitatilor si alocarea resurselor se foloseste o categorie de tehnici care au un element comun: se bazeaza pe reprezentarea proiectului ca o retea de activitati, in care se reflecta toate interdependentele lor temporale. Datorita acestui mod de reprezentare tehnicile sunt cunoscute sub numele de metode ale planificarii in retea.
Tehnicile de planificare in retea isi au originea in a doua parte a deceniului 1950, cand doua grupuri de cercetare, lucrand in paralel si independent, au perfectat metodele care mai tarziu au ramas in literatura de specialitate sub numele de PERT si CPM.
PERT (Program Evaluation and Review Technique) a fost dezvoltata in 1957-1958 de un grup de cercetatori de la Oficiul pentru proiecte speciale ale marinei militare americane, firma de consultanta Booz, Allen si Hamilton si Missiles Systems Division a firmei Lockheed Aircraft, in legatura cu realizarea sistemului de rachete Polaris. Proiectul implica cca 3000 firme si un numar de aproximativ 50000 de activitati; prin aplicarea metodei PERT durata lui a fost scurtata cu 2 ani fata de estimarile initiale. Metoda a fost data publicitatii in septembrie 1959 (Malcolm s.a. [18]).
CPM (Critical Path Method) este rezultatul unei echipe de cercetare constituita de firma du Pont de Nemours din domeniul industriei chimice si firma Remington Rand Univac Division, cu scopul imbunatatirii modului de planificare si urmarire a lucrarilor de revizie si intretinere pentru uzinele chimice. Cercetarile au inceput in 1957, iar prima comunicare a rezultatelor a avut loc la o sesiune stiintifica in decembrie 1959 (Kelley si Walker [17]). Aplicarea metodei CPM la lucrarile de revizie a unei uzine a firmei du Pont a redus durata acestora de la 125 ore la 78.
Din punctul de vedere al reprezentarii retelei si al programarii activitatilor nu exista deosebiri esentiale intre PERT si CPM; acesta este motivul pentru care adesea cele doua denumiri sunt folosite una in locul celeilalte. Totusi, unele diferente exista datorita caracterului diferit al problemelor de la care s-a pornit in elaborarea metodelor. Astfel, elaborata in contextul unui proiect de cercetare-dezvoltare, PERT a trebuit sa tina cont de incertitudinile prezente intr-o astfel de lucrare. Ca urmare, PERT priveste durata totala a proiectului ca fiind o variabila aleatoare si face calculele probabilistice necesare pentru a o caracteriza ca atare. Metoda CPM in schimb, are la baza un proiect constituit in majoritate din operatii de rutina, ale caror durate puteau fi predeterminate, mai mult sau mai putin precis, pe baza de normative; in consecinta, CPM consta din calcule deterministe. Insa, un aspect de deosebit interes pentru realizatorii metodei CPM a fost acela de a reduce durata totala de efectuare a reviziei si reparatiei pentru ca aceasta reprezenta capacitatea de productie pierduta. Pornind de la ideea ca unele activitati din proiect pot fi scurtate daca li se aloca resurse suplimentare, metoda CPM a incorporat si rezolvarea problemei timp-cost in vederea determinarii echilibrului optim intre durata si costul proiectului.
La noi in tara metoda planificarii in retea a inceput sa fie aplicata din anul 1965 in domeniul constructiilor; in anul 1967 un grup de specialisti a intocmit o retea cu 800 de activitati pentru constructia unei nave la Santierul naval Galati (Homos [15]). Ulterior metoda s-a raspandit cuprinzand si alte domenii cum ar fi pregatirea fabricatiei, reparatii de utilaje etc.
Pentru a aplica metoda planificarii in retea trebuie parcurse urmatoarele etape:
- elaborarea retelei; aceasta implica definirea tuturor activitatilor care constituie proiectul, specificarea relatiilor de precedenta-succesiune dintre ele si trasarea retelei;
- programarea activitatilor; pentru aceasta etapa este necesara estimarea duratelor activitatilor. Pe baza acestor durate si a relatiilor de precedenta-succesiune se determina pentru ficare activitate momentele de inceput si de incheiere;
- analiza si alocarea resurselor; aici se cere cunoasterea necesarului de resurse al fiecarei activitati pe de-o parte si disponibilul de resurse pe de alta parte. Este posibil ca disponibilul limitat de resurse alocate proiectului sa faca necesara reprogramarea activitatilor fata de programul intocmit in etapa anterioara. Ori, daca durata totala a proiectului este prea lunga asa cum a fost ea determinata in etapa precedenta, se poate incerca scurtarea ei prin alocarea de resurse suplimentare anumitor activitati in vederea reducerii duratelor lor;
- controlul desfasurarii proiectului; este functiunea prin care se verifica conformitatea executiei cu programul de desfasurare a proiectului. Cand se constata abateri devine necesara revizuirea si actualizarea programului de executie a activitatilor ramase inca neatacate.
2 Elaborarea retelei
Pentru a facilita intelegerea celor ce urmeaza vom conduce intreaga discutie in contextul unui exemplu simplu, usor de vizualizat. Concluziile vor fi destul de generale pentru a permite extrapolarea la proiecte de orice grad de complexitate. Asadar, sa presupunem ca dorim sa construim un garaj pe locul unei magazii vechi din spatele casei.
Tabelul 1. Analiza activitatilor
|
Simbolul activitatii |
Descrierea activitatii |
Predecesori |
|
A |
Demolarea vechi magazii |
|
|
B |
Procurarea materialelor pentru zidarie si pentru armarea betonului |
|
|
C |
Sortarea materialelor rezultate din demolare |
A |
|
D |
Excavarea fundatiilor |
A |
|
E |
Fundarea caii de acces auto |
A |
|
F |
Intocmirea necesarului de alte materiale si procurarea lor |
C |
|
G |
Turnarea fundatiilor din beton armat |
B,D |
|
H |
Turnarea caii de acces auto |
E |
|
I |
Ridicarea zidariei |
B,G |
|
J |
Nivelarea pardoselilor cu balast si turnarea betonului in pardoseli |
F,G |
|
K |
Executarea instalatiei electrice |
F,I |
|
L |
Finisarea peretilor |
K,M,N |
|
M |
Ridicarea acoperisului |
F,I |
|
N |
Finisarea pardoselelor |
J |
|
O |
Instalarea jgheaburilor si burlanelor |
F,M |
|
P |
Evacuarea molozului si curatenie generala |
H,L,O |
Pornim prin a identifica toate activitatile care concura la realizarea proiectului nostru. Dupa aceasta inventariere este necesar sa se stabileasca relatiile de precedenta-succesiune dintre ele, luand fiecare activitate in parte si raspunzad la intrebarea: care activitati trebuie neaparat terminate inainte ca activitatea analizata sa poata incepe? Rezultatele acestei etape, desfasurata pentru proiectul nostru, sunt trecute in tabelul 1 pentru usurinta referirilor ulterioare s-au simbolizat toate activitatile cu litere mari. Din tabel rezulta, de exemplu, ca A este un predecesor al lui C, in timp C este un succesor al lui A.
Sa remarcam ca aceasta faza de analiza a activitatilor constituie conceptia itinerarului tehnologic pentru proiectul dat. Spre deosebire insa de tehnologia de executie a unui reper oarecare, unde operatiile se succed una dupa alta, in cazul de fata unele activitati se pot desfasura simultan (in paralel). Urmeaza de aici ca o activitate poate avea mai multi predecesori.
Trebuie subliniat faptul ca la stabilirea relatiilor de precedenta-succesiune trebuie luata in considerare doar cerinta de natura tehnologica; aspectele legate de derularea in timp a activitatilor nu trebuie sa influenteze aceasta etapa. Spre exemplu, eventualitatea ca aceeasi echipa de muncitori va trebui sa toarne toate structurile de beton nu trebuie sa ne faca sa conditionam inceperea lui H de terminarea lui G; daca aceasta va fi situatia, atunci problema va fi rezolvata in etapa de analiza si alocare a resurselor.
O retea este alcatuita din noduri si arce orientate. Pentru o definitie formala vom apela la cea data de Ford si Fulkerson [11].
Reteua unui proiect consta dintr-un set finit N de n elemente 1,2,.,i,.,j,.,n numite noduri, impreuna cu un subset A de perechi ordonate (i, j) de noduri numite arce. Pentru a trasa o retea se alege un punct corespunzator fiecarui nod i din N si se duce un arc din i spre j daca perechea ordonata (i, j) se gaseste in A.
Atat dupa metodologia CPM cat si PERT arcele retelei reprezinta activitatile proiectului. Arcul (i,j) se desfasoara intre cele doua noduri: nodul i, reprezentand evenimentul de inceput al activitatii, si nodul j desemnand evenimentul de sfarsit (incheiere) al activitatii. Figura 1 a, b si c ilustreaza aceste notiuni.
Diferente apar in modul de inscriere a explicatiilor in retea: in timp ce CPM scrie denumirea activitatilor (sau simbolul aferent) pe arce, PERT inscrie denumirea evenimentelor in noduri (figura 2). Aceasta inseamna ca in CPM controlul desfasurarii proiectului este orientat asupra activitatilor, pe cand in PERT controlul priveste realizarea evenimentelor la timp. In general reprezentarea CPM este mai usor de citit, motiv pentru care se bucura de cea mai larga raspandire si o vom folosi si noi.

Fig. 1 Arce si noduri, activitati si evenimente

Fig.2 Reprezentari CPM si PERT ale activitatilor A, B, C si D din tabelul 1
Pentru trasarea retelei exista un numar de principii care trebuie respectate, reguli impuse fie din considerente de natura logica fie din cauza cerintelor programelor de calculator folosite pentru rezolvarea acestor probleme:
1. lungimea si orientarea arcelor sunt lipsite de semnificatie;
2. nodul are o semnificatie logica: activitatile ale caror arce pleaca din nod nu pot incepe decat dupa ce toate activitatile ale caror arce intra in nod s-au incheiat (vezi figura 2);
3. o retea poate sa aiba un singur nod initial, marcand evenimentul de inceput al proiectului, si un singur nod terminal (final), marcand evenimentul de sfarsit al proiectului. Arcele care pleaca din nodul initial desemneaza activitati initiale, iar cele care intra in nodul final arata activitati terminale;
4. fiecare activitate trebuie sa fie identificata in mod univoc de catre evenimentele sale de inceput si sfarsit; aceasta inseamna ca:
doua noduri nu pot purta acelasi numar;
doua noduri pot fi conectate de cel mult un arc; in acest sens reprezentarea din figura 1.d este gresita.

Fig. 3 Circuit intr-o retea
Aceasta ne permite sa ne referim la o anumita activitate fie prin numele (sau simbolul ei), fie prin perechea de noduri care o incadreaza. De exemplu, activitatea "Sortarea materialelor rezultate din demolare din figura 2.a poate fi identificata drept activitatea C sau activitatea (3,4);
5. nodurile trebuie numerotate astfel incat nodul din care porneste un arc sa aiba numar mai mic decat nodul in care se termina arcul respectiv. Aceasta regula are meritul ca, atunci cand nu poate fi respectata, semnaleaza prezenta unui ciclu inchis (circuit) in retea. Astfel, in figura 3 activitatile F,K,J formeaza un circuit provenind dintr-o eroare de logica. Intr-adevar, prin tranzitivitatea relatiilor de precedenta-succesiune, fiecare activitate din ciclul inchis apare ca fiind un predecesor pentru sine insasi. Existenta circuitului este indicata de imposibilitatea numerotarii nodurilor asociate cu F,K,J in conformitate cu regula 5.

Fig. 4 Utilizarea unei activitati fictive
Respectarea regulilor aratate mai sus poate sa faca uneori necesara folosirea activitatilor fictive. O activitate fictiva are o durata egala cu zero si nu consuma resurse (are cost nul); singurul scop servit de activitatea fictiva este de a exprima relatii de precedenta-succesiune. Ca exemplu, sa consideram patru activitati A,B,C si D interconditionate astfel: pentru ca C sa inceapa trebuie ca A si B sa se incheie (figura 4.a), in timp ce inceperea lui D este conditionata doar de terminarea activitatii B (fig. 4.b). Incercarea de reprezentare unitara a acestor relatii ca in figura 4.c este gresita intrucat conform principiului (2) de mai sus apare ca atat C cat si D trebuie sa fie precedate de A si B. Figura 4.d ofera reprezentarea corecta: cele doua noduri arata ca activitatea C este precedata de A, iar D precedata de B; in plus, activitatea fictiva al carei arc orientat este trasat cu linie intrerupta, exprima faptul ca C este precedata si de B.
 Fig. 5 Prima versiune a
retelei proiectului
Fig. 5 Prima versiune a
retelei proiectului
Tot cu ajutorul activitatilor fictive se rezolva si situatii de felul celor aratate in figura 1.d. Astfel, activitatile K si M din tabelul 1 au pe I ca predecesor comun; in acelasi timp K si M preced, in comun, pe L. Pentru a nu incalca regula conform careia doua noduri pot fi conectate de cel mult un arc, reprezentarea activitatilor se face ca in figura 5 utilizand activitatea fictiva (12, 14). Convenim ca, pentru a le deosebi de activitatile propriu-zise ale proiectului, activitatile fictive sa fie desenate cu linie intrerupta.
Cele discutate pana aici au fost aplicate exemplului nostru din tabelul 1, rezultand prima versiune a retelei aferente (figura 5).
Pentru ca numerotarea nodurilor sa fie conforma cu regula (5), s-a aplicat o procedura data de Fulkerson [12]:
1. se numeroteaza nodul initial cu 1 ;
2. se indeparteaza toate arcele care pleaca din nodurile deja numerotate;
3. se continua numerotarea indentificand toate nodurile care nu au arce incidente si dandu-le numere consecutive in ordine arbitrara ;
4. se repeta pasii 2 si 3 pana cand se numeroteaza si nodul terminal.
Desi, asa cum s-a precizat anterior, directia arcelor nu afecteaza continutul informational al retelei, pentru a usura citirea si intelegerea acesteia este recomandata orientarea generala a arcelor dinspre nodul initial spre cel terminal, adica in sensul curgerii timpului. De asemenea, intrucat costul rezolvarii pe calculator depinde de numarul total al arcelor, se va urmari ca in reprezentarea retelei sa se utilizeze doar strictul necesar de activitati fictive.
O notiune importanta este cea de drum sau cale prin retea, pe care o definim dupa Ford si Fulkerson [11] astfel :
Fie N1, N2 ,.,Ni,.,Nn (n≥2) o succesiune de noduri distincte in asa fel incat fiecare pereche (Ni , Ni+1), i = 1,.,n-1, reprezinta un arc al retelei. Atunci, succesiunea de noduri si arce N1- (N1,N2 ) - N2 -.- (Nn-1, Nn) - Nn formeaza un drum de la nodul N1 la nodul Nn. Astfel, in figura 5 1-A-3-D-5 este un drum intre aceleasi doua noduri 1 si 5, in timp ce 1-B-2-(2,5)-5 este un alt drum intre aceleasi doua noduri. Evident, un drum poate fi complet identificat mai simplu specificand fie doar nodurile prin care trece fie doar activitatile care-l constituie; astfel, in loc de 1-A-3-D-5 putem zice 1-3-5 sau A-D.
Dupa intocmirea retelei in forma ei primara este util sa verificam, si daca exista sa eliminam, relatiile de precedenta redundante. Spre exemplu, in figura 5 este usor de localizat cel putin o redundanta: activitatea fictiva (2,9) nu este necesara pentru a impune pe B ca predecesor al lui I intrucat oricum B precede pe I pe drumul 1-2-5-7-9; ca urmare, (2,9) se poate indeparta din retea.
Sa observam ca, desi atat B cat si G sunt predecesori ai lui I, acest lucru fiind stipulat si in tabelul 1, activitatea G este un predecesor imediat in timp ce B este un predecesor indepartat.
Pentru eliminarea redundantelor putem adopta o procedura data de Wiest si Levy [28].
3 Programarea activitatilor si determinarea drumului critic
Scopul acestei etape este de a determina durata totala a proiectului si momentele de inceput si sfarsit pentru fiecare activitate. Evident, pentru a putea face acest lucru este necesar sa cunoastem duratele activitatilor.
Pentru a facilita intelegerea notiunilor de baza sa consideram mai intai o retea foarte simpla (vezi figura 6.a). Numarul scris la dreapta simbolului activitatii arata durata, sa zicem in zile. Pentru a nu complica lucrurile, pentru programarea activitatilor vom lucra in tot acest capitol numai cu zile intregi (fara fractiuni).
Se observa ca putem parcurge reteaua dinspre nodul initial spre cel final, in sensul derularii activitatilor in timp, pe trei cai B-E-F, care dureaza 7 zile, A-C-F, care dureaza 9 zile si A-D-E-F, care dureaza 8 zile. Drumul de lungime maxima (durata maxima) din retea se numeste drum critic, iar activitatile din care este constituit se numesc activitati critice. La noi drumul critic este A-C-F si este marcat prin arce trasate cu linie groasa.
In figura 6.b s-a presupus ca proiectul incepe la momentul zero si ca fiecare activitate incepe cat mai devreme posibil ; momentul de inceput al activitatii este denumit, in aceasta situatie, inceput avansat si il vom nota cu IA(i,j), cand ne referim la activitatea (i,j). Reteaua a fost reprezentata la scara timpului, adica lungimea fiecarui arc este astfel incat proiectia sa pe axa orizontala sa fie proportionala cu durata activitatii respective. Din figura 6.b se observa ca durata de 9 zile a drumului critic reprezinta cel mai scurt timp in care se poate realiza proiectul.
Intrucat, in general, se cauta inchierea unui proiect cat mai repede posibil, sa stabilim termenul limita de predare pentru ziua 9. Devine imediat evident ca nici o activitate critica nu poate fi intarziata peste inceputul ei avansat. In schimb activitatile necritice ofera o oarecare flexibilitate in programare. Spre exemplu, E poate incepe cu o zi intarziere fara a afecta predarea proiectului la termen (vezi figura 6.c,e). Spunem ca activitatea E dispune de marja (rezerva) de timp.
In ceea ce priveste pe D, si acesta activitate poate fi intarziata cu o zi fata de inceputul ei avansat fara a intarzia proiectul; deci D are marja de timp. Totusi, daca D incepe in ziua 4 (figura 6.f) in loc de ziua 3 (figura 6.b) si activitatea E va trebui sa fie programata cu o zi mai tarziu decat inceputul avansat.
O alta situatie apare in legatura cu activitatea necritica B. Daca o intarziem cu o zi (figura 6.d), activitatea succesoare E nu va fi afectata. Daca intarziem B cu doua zile (figura 6.g), E nu va putea incepe mai devreme decat ziua 6, insa proiectul va fi totusi predat la termen; si B are marja de timp.
Sa mai observam ca in figura 6.i toate activitatile sunt programate cat mai tarziu posibil, respectandu-se conditia de a se inchieia proiectul la termenul stabilit pentru ziua 9. In acest caz fiecare activitate a fost programata la inceputul intarziat, notat IIi,j pentru activitatea (i,j).
Pentru a sistematiza, notam ca, legat de marjele de timp s-au intalnit doua situatii:
- cazul in care o activitate (i,j) poate fi intarziata fara a obliga pe vreunul din succesorii ei sa intarzie fata de inceputul avansat. Marja de timp asociata acestei situatii este marja libera, notata MLi,j. Marjele libere se pot vizualiza pe graficul care reprezinta reteaua la scara timpului cu toate activitatile programate la inceputul avansat (vezi liniile punctate in figura 6.b).
- cazul in care intarzierea activitatii (i,j), desi nu perturba terminarea proiectului la timp, va obliga pe unul sau altul dintre succesorii lui (i,j) sa inceapa mai tarziu decat inceputul avansat. Evident, activitatea (i,j) nu are marja libera dispunand, insa, de un alt fel de flexibilitate in raport cu termenul de predare a proiectului, numita marja totala, notata MTi,j.

Fig. 6 Retea simpla cu reprezentarea activitatilor la scara timpului
Astfel, activitatile B si E au marje libere de cate o zi; activitatea B are marja totala de doua zile, iar D si E au marje totale de cate o zi. Urmeaza ca o activitatea care are marja libera are cel putin tot atata marja totala:
0 ![]() MLi,j
MLi,j ![]() MTi,j
MTi,j
Activitatile critice au marjele totale cele mai mici din intreaga retea, acestea fiind chiar egale cu zero atunci cand termenul de predare al proiectului corespunde cu durata drumului critic.
Sa recapitulam notatiile introduse pana acum si sa le completam cu cele care ne vor mai fi necesare:
IAi,j - inceputul avansat al activitatii (i,j);
IIi,j - inceputul intarziat al activitatii (i,j);
SAij - sfasitul avansat al activitatii (i,j);
SIi,j - sfarsitul intarziat al activitatii (i,j);
MLi,j - marja libera a activitatii (i,j);
MTi,j - marja totala a activitatii (i,j);
Yi,j - durata activitatii (i,j);
Ti - momentul cel mai devreme (momentul avansat) de producere a evenimentului reprezentat de nodul i;
n - indice reprezentand nodul terminal al retelei.
Din figura 6.b rezulta ca pentru a determina inceputul avansat pentru fiecare activitate, se porneste de la momentul de incepere a proiectului, programand apoi fiecare activitate cat mai devreme posibil (adica imediat ce toti predecesorii sai sunt gata).
Intrucat in acest mod se traverseaza reteaua de la nodul 1 pana la nodul n, operatia poarta numele de pasa inainte (in aval) si consta din urmatoarele:
1. inceputul avansat pentru activitatile initiale se face egal cu momentul de inceput al proiectului (de regula momentul zero);
2. pentru urmatoarele activitati se calculeaza in ordine topologica:
IAi,j = max [SA al tuturor predecesorilor activitatii (i,j)]
SAi,j = IAi,j+Yi,j
3. durata minima a proiectului este chiar Tn:
Tn = max [SA al tuturor activitatilor terminale].
Din figura 6.i reiese ca sfarsitul intarziat al fiecarei activitati se poate determina traversand reteaua dinspre nodul terminal spre nodul initial, programand fiecare activitate cat mai tarziu posibil. Acesta este pasa inapoi (in amonte) si consta din:
1. sfarsitul intarziat al activitatilor terminale se face egal cu momentul prestabilit pentru predarea proiectului;
2. se considera celelalte activitati in ordine inversa ordonarii topologice si se calculeaza:
SIi,j = min [II al tuturor succesorilor activitatii (i,j)]
IIi,j = SIi,j-Yi,j .
Pe baza informatiilor de mai sus se pot calcula toate marjele de timp:
marja libera, care reprezinta flexibilitatea de programare a unei activitati in
raport cu succesorii sai directi:
MLi,j = min [IA al tuturor succesorilor imediati ai activitatii (i,j)]-SAi,j;
marja totala, care este masura flexibilitatii de programare a unei activitati in
raport cu termenul de predare a proiectului:
MTi,j = IIi,j - IAi,j = SIi,j - SAi,j.
Tabelul 2 cuprinde rezultatele celor doua pase si marjele de timp pentru reteaua din figura 6.a in ipoteza ca proiectul incepe la momentul zero si trebuie incheiat pana in ziua 9.
Acum vom face calcule similare pentru proiectul nostru de constructie a garajului. In mod normal rezolvarea retelelor se face pe calculator; in absenta acestuia si atunci cand reteaua este de dimensiuni mici, calculele se pot face manual, direct pe retea. In acest scop am atasat fiecarei activitati, inclusiv celor fictive, cate o caseta in care am inscris rezultatele (vezi figura 7); marjele sunt scrise deasupra sau dedesubtul casetei. Pentru activitatile fictive nu s-au calculat marje de timp, nefiind necesare.
Tabelul.2 Rezultatele programarii activitatlor pentru
reteua din figura 6.a (unitatea de timp=1 zi)
|
Activita Tea |
Durata |
Predecesori imediati |
Succesori imediati |
IA |
SA |
II |
SI |
ML |
MT |
|
A |
2 |
|
C,D |
0 |
2 |
0 |
2 |
Act.critica ML1,2=MT1,2 =0 |
|
|
B |
3 |
|
E |
0 |
3 |
2 |
5 |
1 |
2 |
|
C |
5 |
A |
F |
2 |
7 |
2 |
7 |
Act.critica ML2,4=MT2,4 =0 |
|
|
D |
2 |
A |
E |
2 |
4 |
3 |
5 |
0 |
1 |
|
E |
2 |
B,D |
F |
4 |
6 |
5 |
7 |
1 |
1 |
|
F |
2 |
C,E |
|
7 |
9 |
7 |
9 |
Act.critica ML4,5=MT4,5 =0 |
|
In rezolvarea din figura 7 termenul de incheiere a proiectului a fost luat egal cu T13, momentul avansat in nodul 13, adica ziua 25. In cazul ca termenul de incheiere ar fi fost stabilit cu ∆t mai tarziu decat T13, toate marjele totale din retea precum si marjele libere ale activitatilor terminale ar fi rezultat cu acest ∆t mai mari.
Drumul critic, a carui durata reprezinta intervalul minim de timp in care se poate realiza proiectul, se poate determina cu ajutorul marjelor totale. Se sorteaza activitatile in grupe dupa marja totala; in cadrul fiecarei grupe se ordoneaza activitatile crescator, dupa inceputul avansat (vezi tabelul 3).
Tabelul 3 Identificarea drumului critic
|
Activitatea |
MT |
IA |
Drum |
|
A D G I M L P |
0 0 0 0 0 0 0 |
0 2 4 6 14 19 24 |
Drumul critic 1-2-4-6-8-10-11-12-13 |
|
B |
3 |
0 |
Drum subcritic 1-4 |
|
K |
4 |
14 |
Drum subcritic 8-11 |
|
O |
4 |
19 |
Drum subcritic 10-12 |
|
C F |
10 10 |
2 3 |
Drum subcritic 2-3-7 |
|
J N |
10 10 |
6 8 |
Drum subcritic 7-9-11 |
|
E H |
20 20 |
2 3 |
Drum subcritic 2-5-12 |
Grupa de activitati cu marja minima constituie drumul critic, identificat prin arce trasate cu linie groasa din figura 7 ; celelalte grupe formeaza drumuri subcritice. Cu cat marja totala este mai mare cu atat drumul respectiv este mai putin critic. Un drum subcritic nu trebuie sa mearga, in mod necesar, de la nodul initial pana la cel terminal. Sa mai notam ca o retea poate sa contina mai multe drumuri critice.
Din cele de mai sus este clar ca pentru a urgenta terminarea unui proiect este necesara scurtarea activitatilor de pe drumul critic. Dar, dincolo de o anumita limita, reducerea duratelor activitatilor critice poate sa apara ca inoperanta deoarece drumul critic isi schimba traseul de-a lungul unei cai care fusese pana atunci subcritica. Spre exemplu, putem reduce durata proiectului nostru scurtand activitatea M. Cand M ajunge la durata de 1 zi calea 1-2-4-6-8-11-12-13 devine critica si impune o durata minima de 21 zile asupra proiectului (figura 8). Calea 8-11, anterior subcritica, a devenit acum critica; nici o reducere in continuare a activitatii M nu va mai putea scurta proiectul din cauza noii cai critice.
 Fig .7 Calculele de programare a activitatilor
pentru proiectul din tabelul 1(proiectul incepe in momentul zero si are
termen de predare ziua 25)
Fig .7 Calculele de programare a activitatilor
pentru proiectul din tabelul 1(proiectul incepe in momentul zero si are
termen de predare ziua 25)

Fig. 8 Scurtarea proiectului la 21 zile; doua drumuri critice
Daca totusi dorim sa terminam proiectul mai repede putem micsora durata activitatii I pana la 2 zile, cand apare un nou drum critic de 15 zile 1-2-4-6-7-9-11-12-13 (figura 9) incluzand fostul drum subcritic 7-9-11. Din nou, reducerea in continuare a lui I nu-si mai are rostul.
 Fig 9 Scurtarea
proiectului la 15 zile; trei drumuri critice
Fig 9 Scurtarea
proiectului la 15 zile; trei drumuri critice
4. Analiza si alocarea resurselor
In cele discutate pana aici privind programarea activitatilor unui proiect nu am fost in nici un fel preocupati de problema resurselor implicate; toate restrictiile luate in considerare au fost numai de natura tehnologica.
In acesta sectiune ne vom referi la analiza necesarului de resurse si la alocarea acestora, pornind de la premiza ca resursele ce intervin in desfasurarea proiectului pot influenta programarea activitatilor fie prin disponibilitatea lor limitata, fie prin alte feluri de conditii.
Prin resurse intelegem, in mod generic, mijloacele materiale, financiare si resursele umane. O activitate poate utiliza una sau mai multe resurse, sau una si aceeasi resursa poate fi solicitata simultan de mai multe activitati care se desfasoara in paralel.
Costurile asociate cu executia unui proiect se pot imparti in doua categorii:
- costurile directe; ele pot fi urmarite direct pe fiecare activitate, cum ar fi: materialele directe, costul utilizarii echipamentelor specifice activitatii, manopera directa;
- costurile indirecte, legate de conducerea si deservirea intregului proiect, nu pot fi imputate direct vreunei activitati anume; exemple: cheltuielile de regie, penalizarile pentru nerespectarea termenelor de predare.
Este evident ca, de regula, costurile indirecte cresc o data cu durata proiectului. In schimb, daca ne referim la costurile directe, in general este mai costisitor sa se realizeze o activitate in timp scurt decat in timp lung. Urmeaza de aici ca executia rapida a unui proiect antreneaza, pe de o parte, costuri directe mari, permitand, pe de alta parte, economii la costurile indirecte.
In tabelul 4 se prezinta principalele tipuri de probleme de analiza si alocarea resurselor intalnite in literatura de specialitate. In cele ce urmeaza vom discuta asupra fiecarui tip in parte.
Problema analizei necesarului de resurse urmareste stabilirea perioada-de-perioada a consumului de resurse corespunzator unei anumite programari a activitatilor proiectului. Analiza se poate materializa sub forma unui grafic ca in figura 10; cand se utilizeaza mai multe resurse trebuie sa se construiasca mai multe grafice, cate unul pentru fiecare din ele. Aceste grafice se pot folosi in diferite feluri; astfel, se poate stabili daca pe timpul executiei proiectului necesarul nu depaseste disponibilul sau, cand avem mai multe alternative de programare a activitatilor, se poate face o comparatie privind eficienta utilizarii resurselor in fiecare alternativa.
Problema de nivelare a resurselor are ca obiect de activitate preintampinarea fluctuatiilor mari ale necesarului de resurse de la o perioada la alta. Uniformizarea consumului de resurse in perioada de desfasurare a proiectului are, in general, efecte favorabile asupra costurilor. Daca luam ca exemplu consumul de munca vie, o utilizare constanta a resurselor umane duce la diminuarea sau eliminarea completa a cheltuielilor legate de plata orelor suplimentare, reduce timpii de stagnare, reduce sau elimina incadrarea de personal sezonier etc.
Pentru a exemplica consideram in figura 10 o retea, trasata la scara timpului, in care numerele inscrise in paranteze drepte arata necesarul de muncitori pentru fiecare activitate. Programarea initiala (figura 10 a) evidentiaza fluctuatii considerabile ale necesarului de resurse umane cu o culminatie in ziua a treia. Prin reprogramarea activitatilor in limitele marjelor lor de timp se poate obtine un alt profil temporal al utilizarii resurselor umane, mult aplatisat fata de situatia anterioara (figura 10 b).
Pentru retele simple si cand se ia in considerare doar o singura resursa nivelarea se poate face manual. In cazul retelelor complicate, cu utilizarea mai multor resurse, trebuie sa se faca apel la calculator.
Tabelul 4 Clasificarea problemelor de analiza si alocarea resurselor in retele
|
Clasa de probleme |
Ipoteze |
Obiectiv |
|
|
Probleme de analiza a necesarului de resurse |
|
Pentru o programare data a activitatilor proiectului se determina profilul temporal al necesarului din fiecare tip de resurse |
|
|
Probleme de alocare a resurselor |
Probleme de nivelare a resurselor |
-Resursele sunt considerate nelimitate -Duratele activitatilor sunt fixe si cunoscute -Termenul de finalizare a proiectului este prestabilit |
Termenul prestabilit de finalizare a proiectului trebuie respectat. Se cauta acea programare a activitatilor care conduce la un necesar de resurse cat mai uniform pe durata desfasurarii proiectului, adica cu fluctuatii minime de la o perioada la alta |
|
Probleme cu resurse limitate avand drept criteriu durata proiectului |
-Resursele sunt limitate, disponibilul din ficare resursa fiind cunoscut -Duratele activitatilor sunt fixe si date |
Se cauta acea programare a activitatilor care permite executia proiectului in timp minim |
|
|
Probleme cu resurse limitate avand drept criteriu costurile totale |
-Resursele sunt limitate, disponibilul din fiecare resursa fiind cunoscut -Duratele activitatilor sunt variabile intre un minim si un maxim, functie de volumul de resurse alocat |
Se cauta duratele activitatilor si programarea lor care sa permita executia proiectului la cost total (direct + indirect) minim |
|
|
Probleme de optimizare timp- cost |
-Resursele sunt considerate nelimitate -Duratele activitatilor sunt variabile intre un minim si un maxim, functie de volumul de resurse alocat -Termenul de finalizare a proiectului este prestabilit |
Se cauta duratele activitatilor si programarea lor care sa permita executia proiectului la cost direct minim |
|

Fig. 10 Nivelarea utilizarii fortei de munca
Probleme cu resurse limitate urmaresc alocarea resurselor in limita disponibilului, astfel incat programarea activitatilor care se obtine sa fie optima in raport cu unul din urmatoarele doua obiective:
- proiectul sa fie finalizat in timpul cel mai scurt;
- proiectul sa fie realizat la un cost total minim (cost total = costuri directe + costuri indirecte).

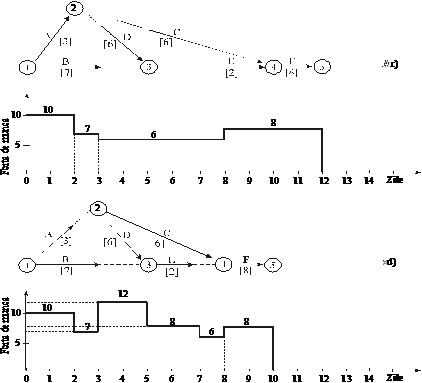
Fig. 11. Reprogramarea proiectului pentru respectarea restrictiei privind forta de munca
Pentru a realiza implicatiile resurselor limitate asupra programarii proiectului sa reconsideram reteaua din figura 10 si sa admitem ca numarul de muncitori disponibili zilnic este de 12. Evident ca, in lumina acestei restrictii, programarea din figura 10 b nu poate fi pusa in aplicare din cauza ca in ziua a treia nu dispunem de cei 13 muncitori necesari; ca urmare proiectul nu poate fi terminat in 9 zile.
In figura 11 sunt aratate trei alternative de reprogramare a activitatilor in vederea respectarii restrictiei impuse; fiecare alternativa asigura alta durata de realizare a proiectului si alt profil temporal al necesarului de resurse umane. In situatia in care urmarim primul dintre criteriile enuntate mai sus vom alege varianta din figura 11.a, 10 zile fiind termenul minim de finalizare a proiectului atunci cand avem la dispozitie doar 12 muncitori. Trebuie sa precizam ca solutia din figura 11.a pentru minimizarea duratei proiectului nu este unica, existand si alte moduri de a executa proiectul in 10 zile cu 12 muncitori; unul din acestea este aratat in figura 11.d.
Am insistat asupra existentei numarului mare de variante in programarea unuia si aceluiasi proiect pentru a sublinia natura combinatorie a problemelor de programare a activitatilor. In situatia proiectelor cu multe activitati in care intervin si restrictii asupra resurselor, determinarea programarii optime a activitatilor este extrem de dificila tocmai din cauza varietatii largi de combinatii posibile. De aceea, asa cum am vazut de altfel procedandu-se si in cazul altor probleme de combinatorica cum sunt cele de ordonantare, pentru gasirea solutiei se apeleaza la metode euristice care, desi nu garanteaza obtinerea optimului matematic, aproximeaza optimul suficient de bine si necesita timpi de calculator ce se mentin in limite acceptabile. Pentru o discutie pe marginea acestor tehnici se pot consulta Davis si Petterson [7], Davis [8].
Sa consideram acum reteaua din figura 12 pentru a intui optimizarea in raport cu cel de-al doilea criteriu, cel al costului total minim. Executia fiecarei activitati nu mai este caracterizata printr-o durata unica ci, functie de volumul de resurse alocat activitatii respective, durata ei poate lua valori intr-un interval cuprins intre o durata minima si una maxima.

Fig. 12 Retea cu duratele activitatilor variabile
A aloca resurse mai multe inseamna a creste costul direct astfel incat putem vorbi despre o dependenta intre durata activitatii si costul ei direct; pentru simplitate s-a admis aceasta dependenta ca fiind liniara si este reprezentata grafic in dreptul fiecarei activitati din retea. S-a calculat, de asemenea, cu cat creste costul direct atunci cand durata activitatii se reduce cu o zi, cifra rezultata fiind inscrisa pe fiecare grafic. Asa, spre exemplu, activitatea A se executa in mod normal (prin tehnologia cea mai eficienta economic) in 18 zile la un cost direct de 400.000 lei; durata ei se poate reduce pana la 15 zile, costul direct fiind in acest caz mai ridicat, si anume 700.000 lei. Aceasta inseamna ca fiecare reducere a duratei cu o zi atrage o crestere a costului direct cu 100.000 lei.
De asemenea, sa mai retinem ca fiecare zi de desfasurare a proiectului implica un cost fix de 100.000 lei, reprezentand costul indirect (toate costurile sunt valori conventionale, valorile lor absolute fiind lipsite de vreo semnificatie).
Problema de rezolvat este aceea de a determina duratele activitatilor din retea, precum si programarea lor astfel incat costul total (direct + indirect) al proiectului sa fie minim. Observam ca, deocamdata, nu am impus restrictii asupra disponibilului de resurse.
Am rezolvat problema in 4 etape, aratate in tabelul din figura 12. Am inceput prin a considera toate activitatile la durata normala si deci cost direct minim. Am stabilit ca drumul critic este B-C, durata proiectului fiind de 20 zile. Suma costurilor directe este 1.500.000 lei, costurile indirecte se ridica la 2.000.000 lei, iar costul total este 3.500.000. Procedam la scurtarea proiectului pentru a observa evolutia costurilor. Evident ca activitatea C este cea a carei durata trebuie redusa mai intai intrucat ea este critica si in acelasi timp asigura cresterea de cost direct cea mai mica. Astfel, in etapa II scurtam pe C la 4 zile, moment in care si activitatea A devine critica, iar costul total este 3.360.000. In etapa III continuam sa reducem tot pe C pana la minimum, adica 3 zile, si, din necesitate, pe A la 17 zile. Costul total urca la 3.390.000. Mai reducem cu o zi durata intregului proiect, scurtand de data aceasta atat pe A cat si pe B, costul total devine 3.440.000. Ne oprim aici din cauza tendintei evidente de crestere a costului total. Solutia optima este cea corespunzatoare etapei II in care toate activitatile sunt critice si nu au marja de timp.
La modul general dependenta costurilor de durata proiectului este reprezentata in figura 13.
Curba costurilor directe minime este segmentata ca urmare a faptului ca reducerea duratei proiectului pana la un punct se realizeaza scurtand un anumit drum critic, de unde reducerea in continuare a duratei se obtine prin scurtarea altui drum critic etc. Denumirea de curba a costurilor directe minime provine din faptul ca, pentru a ne mentine pe ea, scurtarea proiectului se face totdeauna in modul cel mai eficient, adica reducand durata acelei activitati critice care aduce cresterea minima a costului direct. Se observa evolutia inversa a celor doua categorii de costuri in raport cu durata proiectului; in figura este indicata si durata careia ii corespunde costul total minim.

Fig.13 Dependenta dintre costuri si durata proiectului
Evident, introducerea de restrictii asupra disponibilului de resurse complica rezolvarea problemei foarte mult intrucat o resursa insuficienta poate cere ca unele activitati sa inceapa mai tarziu sau sa dureze mai mult. Titlurile bibliografice de mai jos, Davis si Patterson [7] si Davis [8], precum si Moder si Phillips [20] pot fi consultate pentru o discutie mai larga.
Problema de optimizare timp-cost adopta ipoteza, pe care noi am mai intalnit-o, conform careia executia unei activitati poate fi grabita daca acesteia i se aloca un volum sporit de resurse. Acest fapt poate fi vizualizat sub forma unei curbe cost direct-durata (figura 14).

Fig. 14 Curba cost direct-durata pentru activitatea(i,j)
Din motive tehnologice durata activitatii nu poate fi redusa sub o anumita limita pe care am notat-o in figura ca fiind "executia in asalt". Mai exista si un alt punct, pe care l-am numit "executia normala", care corespunde realizarii activitatii prin tehnologia cea mai eficienta din punct de vedere economic. Cele doua puncte au asociate duratele di,j, respectiv Di,j. Prelungirea executiei dincolo de Di,j poate sa duca la o crestere a costului direct. De aceea ne intereseaza doar partea centrala a curbei, cuprinsa intre di,j si Di,j.
In exemplul dat anterior ne-a interesat sa gasim acele durate ale activitatilor si programarea lor care minimizeaza costul total. De multe ori in practica, insa, formularea problemei difera in sensul ca durata de realizare a proiectului este impusa, de exemplu, pe baza prevederilor contractuale. In acest caz costurile indirecte sunt fixate, iar ceea ce noi putem infuenta sunt doar costurile directe.
Ca urmare, problema de optimizare timp-cost se enunta astfel: fiind data o durata D a proiectului (vezi figura 14) si resurse nelimitate, sa se gaseasca duratele activitatilor si programarea lor care asigura executia proiectului cu costuri directe minime.
Esenta acestei probleme poate fi inteleasa usor daca ne referim din nou la exemplul din figura 12. Sa admitem ca se cere realizarea proiectului in 17 zile. Asa cum spuneam, costul indirect este fixat si egal cu 1.600.000 lei. In ceea ce priveste costurile directe pentru intreg proiectul, ele sunt minime si egale cu 1.840.000 lei, atunci cand durata activitatii A este de 17 zile, a lui B 13 zile si a lui C 3 zile. Sa observam ca proiectul poate fi executat in 17 zile si daca durata lui A este 17 zile, a lui B 10 zile si a lui C 6 zile, dar costul direct ar fi mai ridicat.
Acest exemplu a putut fi rezolvat manual datorita dimensiunilor sale reduse. Pentru retele complexe putem folosi o abordare formala a problemei modeland-o ca program liniar. Pentru aceasta aproximam curba cost direct - durata prin coarda trasata cu linie intrerupta in figura 14. Aceasta aproximare liniara prezinta o crestere a costului direct cu ai,j pentru fiecare reducere a duratei activitatii cu o unitate de timp. Duratei Yi,j a activitatii (i,j) ii corespunde un cost direct Ci,j.
Costurile directe totale ale proiectului se obtin insumand costurile directe ale tuturor activitatilor:
![]()
Intrucat
toti wi,j sunt niste constante, a minimiza costurile
directe totale este echivalent cu a maximiza:
![]()
Ca urmare, formularea problemei timp - cost este:
s.c. Ti + Yi,j - Tj ≤ 0 (1)
Yi,j ≤ Di,j (2)
-Yi,j ≤ -di,j (3)
Tn-T1 ≤ D (4)
Am notat cu Ti inceputul avansat in nodul i; n este nodul terminal al retelei. Toti Yi,j si Ti sunt variabile de decizie.
Conditia (1) modeleaza relatiile de precedenta - succesiune dintre activitati, aratand ca nici o activitate al carei arc pleaca din nodul j nu poate incepe inainte ca activitatea (i,j) sa inceapa si sa se desfasoare. Conditiile (2) - ( 3) impun ca durata Yi,j sa fie cuprinsa intre cele doua puncte extreme ale curbei cost direct - durata. Diferenta (Tn-T1) reprezinta durata totala a proiectului, iar (4) exprima conditia ca aceasta durata sa nu depaseasca maximul impus D.
Prin rezolvarea modelului se obtin duratele activitatilor si valorile inceputurilor avansate in toate nodurile; pe baza lor se poate intocmi programul optim de desfasurare a proiectului.
5. Utilizarea calculatorului in managementul proiectului
Pe piata software-ului exista o gama foarte larga de programe de calcul care pana la urma realizeaza acelasi lucru, si anume gestionarea proiectelor. Diferentele dintre ele constau in facilitatile pe care le prezinta fiecare in crearea si urmarirea proiectelor, in elaborarea rapoartelor referitoare la acestea. Printre cele mai folosite programe de calcul se numara: Harvard Total Project (Software Publishing Corporation), Microsoft Project (Microsoft Corporation), Primavera (Primavera Systems Inc.), Super Project Expert (Computer Associates) si altele. Aceste programe permit urmarirea unui proiect in diferitele lui faze: conceptie, realizare si urmarire.
In continuare vom aborda aspectele teoretice de gestiune a unui proiect si de asigurare a urmaririi lui utilizand programul Microsoft Project.
5.1. Sistemul de informatii al proiectului
Programul Microsoft Project (MP) este construit in jurul unui sistem informatic care contine totalitatea elementelor unui proiect.
Schema din figura 17.6 arata organizarea informatiilor.
 Informatii generale despre proiect
Informatii generale despre proiect
Nume
Societate
Date de inceput
Nume responsabil
Costuri etc.
![]() Calendarul proiectului
Calendarul proiectului

Activitati Resurse
Nume Nume
Durata Cantitate
Constrangeri Disponibilitate
Etc. Etc.

Atribuirea de resurse activitatilor
![]()
Fig. 15 Organizarea informatiilor
Organizarea informatiilor proiectului sub forma unei baze de date permite vizualizarea proiectului sub diferite forme.
Datele sunt gestionate dinamic de MP: inserarea unei noi activitati sau a unei noi resurse va fi imediat vizibila in afisarile corespunzatoare.
5.2 Functiile MP
Planificare;
Urmarirea proiectului;
Vizualizarea glisarilor;
Gestiunea resurselor.
MP permite manipularea grafica a datelor cu mouse-ul (durata unei etape, procentul de realizare, crearea de legaturi intre etape).
Sunt disponibile diferite mijloace pentru: vizualizarea lucrului cu resursele, supravegherea supra-utilizarilor sau sub-utilizarilor, urmarirea costurilor etc.
MP dispune de numeroase posibilitati pentru furnizarea informatiilor necesare diferitelor nivele de analiza.
Functiile multi-proiect disponibile permit rezolvarea cerintelor:
partajarea resurselor intre mai multe proiecte;
notiunea de sub-proiect: un proiect este definit in interiorul altuia, ca si cum ar fi o macroactivitate;
legatura intre doua activitati din doua proiecte diferite.
5.3. Ecranele MP
MP dispune de numeroase ecrane de afisare, care permit examinarea proiectului din diferite unghiuri. Cele mai representative sunt:
Gantt: afiseaza lista activitatilor si derularea lor in timp;
Calendar: permite vizualizarea programului de lucru sub forma unui calendar;
PERT: afiseaza relatiile de conditionare dintre activitati intr-un grafic retea;
Resource Graph: pune la dispozitie histogramele de resurse;
Resource Sheet: afiseaza tabelul ce contine informatiile specifice resurselor;
Resource Usage: permite vizualizarea incarcarii resurselor intr-un tabel, in timp.
5.4. Rapoartele MP
MP pune la dispozitie patru categorii de baza de rapoarte:
rapoarte despre activitati;
rapoarte despre resurse;
rapoarte de tip calendar lunar;
rapoarte tabelare.
Ele sunt grupate dupa natura informatiilor pe care le contin, astfel:
rapoarte generale;
rapoarte despre activitatile curente;
rapoarte despre costuri;
rapoarte despre alocarea resurselor;
rapoarte despre incarcarea resurselor.
Toate afisarile pot fi personalizate dupa gustul si nevoile utilizatorului. MP permite:
schimbarea fontului;
modificarea marimii coloanelor;
adaugarea/stergerea de coloane;
modificarea prezentarii grafice.
5.5. Etapele gestionarii proiectului cu MP
Gestiunea proiectului se imparte in doua etape principale.
Ante-proiect
Este un proces iteractiv care permite diferitilor participanti sa se opreasca asupra unei planificari initiale. Aceasta planificare priveste atat stabilirea activitatilor cat si definirea resurselor si afectarea lor, activitatilor proiectului. Finalul acestei etape este definirea proiectului in termeni de costuri, volum de munca si durata.
Urmarirea realizarii proiectului
Acest proces intervine pe parcursul intregii vietii a proiectului si consta in:
culegerea datelor si incorporarea acestora in sistemul informatic;
reactualizarea planificarii pentru activitati in curs sau neincepute.
Etapele principale
5.5.1. Definirea calendarului
Se definesc:
ziua standard de munca;
saptamana standard;
exceptiile (zilele de sarbatoare).
5.5.2. Caracteristicile generale ale proiectului
Se introduc datele generale despre proiect.
Informatii importante:
data de inceput a proiectului;
data de incheiere a proiectului;
modul in care se face calculul termenelor caracteristice (atunci cand se cunoaste data de inceput a proiectului si se doreste determinarea datei de incheiere a acestuia, atunci cand se cunoaste data de incheiere a proiectului si se doreste determinarea datei de inceput a acestuia);
calendarul de baza a proiectului;
informatii generale despre proiect.
Informatii utile:
titlul proiectului;
subiectul proiectului;
numele persoanei care introduce informatiile despre proiect;
numele managerului proiectului;
cuvinte cheie atasate proiectului;
informatii aditionale despre proiect.
5.5.3. Introducerea activitatilor
Se introduc activitatile componente ale proiectului.
Informatii importante:
numele;
durata;
predecesorii;
tipurile de legaturi.
La sfarsitul acestei etape se obtine planificarea desfasurarii activitatilor, drumul critic etc.
Documente importante:
diagrama Gantt,
reteua PERT,
tabelul cu activitatile,
raportul activitatilor,
raportul activitatilor periodice.
5.5.4. Introducerea resurselor
Se introduc resursele necesare desfasurarii proiectului.
Informatii importante:
nume;
capacitate;
costuri;
calendarul resurselor.
Documente importante:
- tabelul resurselor.

![]() Definirea
Definirea
![]() calendarului
calendarului

Caracteristicile
generale ale
![]() proiectului
proiectului

Introducerea
![]() activitatilor
activitatilor

![]() Introducerea
Introducerea
resurselor

![]() Introducerea
Introducerea
![]() alocarilor
alocarilor
![]()
![]()
 Stabilirea
Stabilirea
planificarii
initiale
![]()

Introducerea
datelor reale

Actualizarea
proiectului
![]()
![]() Analiza
Analiza
abaterilor
![]()
Fig. 16 Planificarea initiala si urmarirea proiectului
5.5.5. Alocarea resurselor
Se aloca activitatilor elementare resursele corespunzatoare.
Informatii importante:
numele;
unitati alocate.
Documente interesante:
axate pe activitati:
o tabelul activitatilor;
o raportul activitatilor.
axate pe resurse:
o utilizarea resurselor;
o graficul resurselor;
o tabelul resurselor;
o afisare combinata;
o raportul resurselor.
axate pe proiect:
o raportul rezumat al proiectului.
5.5.6. Stabilirea planificarii initiale
Pastreaza imaginea planificarii pentru efectuarea compararilor ulterioare (analiza abaterilor).
5.5.7. Introducerea datelor aferente desfasurarii proiectului
Se introduc datele referitoare la desfasurarea proiectului.
5.5.8. Analiza abaterilor
Se compara datele referitoare la desfasurarea proiectului cu planificarea initiala.
17.6.5.9. Actualizarea previziunilor
Permite sa se tina cont, la nivelul previziunilor, de ceea ce s-a finalizat in proiect si sa se reajusteze previziunile, daca este cazul, pentru activitatile care nu au inceput sau sunt in curs de executie.
6. Managementul proiectelor multiple
Un proiect multiplu este alcatuit din proiecte care sunt interconectate intre ele. Urmarirea acestora se face cu mare greutate atunci cand la realizarea lor au fost luate in evidenta un numar mare de activitati.
Existenta unor astfel de proiecte complexe, de mare anvergura, cu durate mari de executie si cu consumuri semnificative de resurse umane, materiale si echipamente, cer o gestionare cat mai eficienta din partea echipelor de conducere.
Toate programele de calcul din domeniul managementului au abordat acest aspect al proiectelor complexe, oferind facilitati de gestionare din ce in ce mai precisa a acestora. Proiectantii Microsoft Project-ului au abordat si ei acest aspect. Astfel, Microsoft Project pune la dispozitie o gama larga de posibilitati de creare si urmarire a proiectelor multiple.
Calea cea mai directa de gestionare a proiectelor multiple o reprezinta introducerea informatiilor intr-un singur fisier. Aceasta conduce insa la ingreunarea lucrului si la aparitia conflictelor de resurse. De aceea, solutia cea mai comoda este impartirea lui in proiecte mai mici, mai usor de urmarit, pe faze, utilizand subproiectele. Un subproiect este un grup de activitati salvate intr-un fisier proiect, dar reprezentand o singura activitate intr-un proiect mare, numit proiect principal. Crearea unui subproiect se face in acelasi mod in care se creeaza orice proiect de sine statator, diferenta consta in aceea ca, subproiectul este interconectat intr-un anumit mod cu un alt proiect, proiectul principal. El reprezinta elementul central de control in cadrul unui proiect multiplu. Toate informatiile corespunzatoare subproiectului alimenteaza proiectul principal, permitand actualizarea periodica. In mod automat, schimbarile din proiectul principal sunt reflectate in cadrul subproiectelor.
Recomandari bibliografice
1. Adam,E.E., Ebert,R., Managementul productiei si al operatiunilor. Ed. Teora, Bucuresti, 2001.
2. Candea,D., Abrudan,I., Organizarea si conducerea intreprinderilor industriale. Institutul Politehnic Cluj-Napoca, 1984.
3. Clark,C.E., The Greatest of Finite Set of Random Variables. In "Operations Research", Vol.9, No.2, 1961, p.145-172.
4. Clark,C.E., The PERT Model for Distribution of an Activity Time In "Operations Research", Vol.10, No.3, 1962, p.405-406.
5. Crowston,W, Thompson,G.L., Decision CPM: A Method for Simultaneous Planning, Scheduling and Control of Projects In "Operations Research", Vol.15, No.3, 1967, p.407-426.
6. Danet,A., Managementul proiectelor. Editura Disz Tipo, Brasov, 2001.
7. Davis,E.W., Patterson,J.H., A Comparison of Heuristic and Optimum Solutions in Resource-Constrained Project Scheduling In "Management Science", Vol.21, No.8, 1975, p.944-955.
8. Davis,E.W., Project Management: Network-Based Scheduling Techniques. In Hax,A.C. (coordonator), "Studies in Operations Management". North-Holland, New York, 1978.
9. Davis,R., Vickery,S., Markland,R., Operations Management. Concepts in Manufacturing and Services 2 nd edition, International Thomson Publishing, USA, 1998.
10. Fondahl,J.W., A Non-Computer Approach to the Critical Path Method for the Construction Industry Technical Report No.9, Construction Institute, Stanford University, 1962.
11. Ford,L.R., Fulkerson,D.R., Flows in Networks. Princeton University Press, Princeton, New Jersey, 1974.
12. Fulkerson,D.R., Expected Critical Path Lengths in PERT Networks In "Operations Research", Vol.10, No.6, 1962, p.808-817.
13. Hax,A.C., Candea,D., Production and Inventory Management. Prentice-Hall, Englewood Cliffs, New Jersey, 1984.
14. Heizer,J., Render,B., Production and Operations Management Allgue and Bacon Boston, 1993.
15. Homos,T., Programarea si conducerea operativa in retea a proceselor complexe (Metoda drumului critic si PERT) Litografia Institutului Politehnic Bucuresti, 1981b.
16. Kaufmann,A., Desbazeille,G., Metoda drumului critic Ed. Tehnica, Bucuresti, 1971.
17. Kelley,J.E.Jr., Walker,M.R., Critical Path Planning and Scheduling. In "Proceedings of the Eastern Joint Computer Conference", Boston, decembrie 1959.
18. Malcolm,D.G., Roseboom,J.H., Clark,C.E., Fazar,W., Applications of a Technique for Research and Development Program Evaluation In "Operations Research", Vol.7, No.5, 1959, p.649-669.
19. Mihoc,Gh., Micu,N.,Introducere in teoria probabilitatilor Editura Tehnica, Bucuresti, 1970.
20. Moder,J.J, Phillips,C.R., Project Management with CPM and PERT, Van Nostrand Reinhold, New York, 1970.
21. Moeller,G.L., Digman,L.A., Operations Planning with VERT. In "Operations Research", Vol.29, No.4, 1981, p.676-697.
22. Moldoveanu,G., Managementul operational al productiei Ed. Economica, Bucuresti, 1996.
23. Pritsker,A.B., Happ,W.W., GERT: Graphical Evaluation and Review Technique, Part I: Fundamentals. In "Journal of Industrial Engineering", Vol.17, No.5, 1966, p.267-274.
24. Pritsker,A.B., Whitehouse,G.E., GERT: Graphical Evaluation and Review Technique, Part II: Probabilistic and Engineering Applications. In "Journal of Industrial Engineering", Vol.17, No.6, 1966, p.293-299.
25. Prostean,G., Management prin proiect. Editura Orizonturi universitare, Timisoara, 2001.
26. Starr,M.K., Conducerea productiei. Sisteme si sinteze. Editura Tehnica, Bucuresti, 1970.
27. Van Slyke,R.M., Monte Carlo Methods and the PERT Problem. In "Operations Research", Vol.11, No.5, 1963, p.839-860.
28. Wiest,J.D., Levy,F.K., A Management Guide to PERT/CPM: with GERT/PDM/DCPM and Other Networks. Prentice-Hall, Englewood Cliffs, New Jersey, 1977.
29. *** www.microsoft.com/office/projet.
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
||||||||||
|
||||||||||
|
||||||||||
Referate pe aceeasi tema
| ||||||||||
|
| ||||||||||
|
||||||||||
|
|
||||||||||








