
| Aeronautica | Comunicatii | Drept | Informatica | Nutritie | Sociologie |
| Tehnica mecanica |
Tehnica mecanica
|
|
Qdidactic » stiinta & tehnica » tehnica mecanica Dinamica mecanismului motor |
Dinamica mecanismului motor
Dinamica mecanismului motor
Fortele din mecanismul motor
Date initiale:
- viteza unghiulara a arborelui cotit, ω=502,64 rad/s;
- coeficientul de compactitate al motorului, λ=0,300847;
- lungimea bielei, l=118 in mm;
- alezajul cilindrului, D=75 in mm;
 - diagrama indicata a
motorului, p=p(v);
- diagrama indicata a
motorului, p=p(v);
- numarul de timpi, τ=4;
- numarul cilindrilor motorului, i=4.
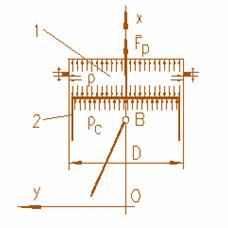
Figura 3.1.4. Forta de presiune a gazelor din cilindru:
1 - spatiul de ardere; 2 - piston.
Forta de presiune a gazelor din cilindru:
Asupra pistonului mecanismului motor actioneaza presiunea gazelor din spatiul de ardere si din carterul motorului, figura 3.1.4.
Forta de presiune Fp se determina cu relatia:
![]()
20
unde: pc este presiunea gazelor din carterul motorului (pc= 0,1 MPa); p este presiunea gazelor din cilindrul motorului, conform diagramei indicate.
Pozitia pistonului in cilindru si forta de presiune Fp sunt functie de unghiul α de rotatie al arborelui cotit. Trecerea presiunii din coordonate p-V (diagrama indicata) in coordonate p-α se face analitic pe baza urmatoarelor relatii:
![]() 21
21
in care: px este presiunea din diagrama indicata corespunzatoare volumului Vx din cilindru, Vc este volumul minim ocupat de fluidul motor (determinat la calculul termic), iar SB este cursa pistonului.
Fortele de inertie:
Fortele de inertie sunt produse de masele in miscare accelerata. In cadrul mecanismului motor grupul piston executa o miscare de translatie alternativa, manivela o miscare de rotatie, iar biela o miscare plan-paralela.
Numai masele mA si mB produc forte de inertie.

Figura 3.1.5. Masele concentrate ale mecanismului
manivela - piston
Concentrarea masei manivelei:
Masa manivelei este concentrata in 2 puncte astfel, figura 3.1.6.:
- masa manivelei concentrata in punctul O, mcO=mO, nu produce forta de inertie;
- masa manivelei concentrata in punctul A, mcA, centrul fusului maneton, se calculeaza cu relatia:
![]() 22
22
unde: mc-masa manivelei (cotului);
rc-distanta de la centrul de greutate al cotului pana la punctul O;
mm-masa fusului maneton; mbr-masa unui brat al manivelei;
rbr-distanta de la centrul de greutate al bratului pana la punctul O.

Figura 3.1.6. Concentrarea masei manivelei in doua puncte,
Gc-centrul de greutate
Deoarece mc, mm, mbr, rc
si rbr nu sunt cunoscute la aceasta faza a
proiectarii motorului, masa mcA se determina din
literatura de specialitate in functie de masa relativa ![]() =13..20 g/cm2 concentrata in punctul A:
=13..20 g/cm2 concentrata in punctul A:
![]() =16,8 g/cm2
=16,8 g/cm2
![]() =16.8*52,8*10-3=0,887 kg23
=16.8*52,8*10-3=0,887 kg23
in care ![]() , in kg/m2 sau g/cm2, este masa
relativa a cotului, iar Ap este aria capului pistonului,
, in kg/m2 sau g/cm2, este masa
relativa a cotului, iar Ap este aria capului pistonului,
Ap=πD2/4=52,8 cm2
Concentrarea masei bielei:
Neglijand momentul rezidual al fortelor de inertie, masa bielei poate fi concentrata in 2 puncte, figura 3.1.7.:
- masa bielei concentrata in punctul A (centrul fusului maneton), mbA, este data de relatia:
![]() =0,510*0,725=0,370 kg24
=0,510*0,725=0,370 kg24
unde: mb- masa bielei, iar lp- pozitia centrului de masa al bielei fata de punctul B;
- masa bielei concentrata in punctul B (axul boltului pistonului), mbB, este data de relatia:
![]() =0,510-0,370=0,14 kg25
=0,510-0,370=0,14 kg25
Daca exista fizic biela unui motor ales ca model, atunci masa mb se determina prin cantarire, iar lp prin cantarire diferentiala sau prin metoda pendulului [28]. De regula, masa bielei si pozitia centrului de greutate nu este cunoscuta. Masa bielei mb se determina in functie de masa relativa a acesteia:
![]() =9,67*52,8*10-3=0,510 kg26
=9,67*52,8*10-3=0,510 kg26
in care ![]() =9,67 g/cm2 este masa relativa a bielei in
kg/m2 sau g/cm2.
=9,67 g/cm2 este masa relativa a bielei in
kg/m2 sau g/cm2.
Pozitia centrului de greutate lp sau rapoartele lp/l, (l-lp)/l se aleg in functie de destinatia motorului sau caracteristicile constructive ale acestuia. Astfel, pentru majoritatea motoarelor ce echipeaza autovehiculele rutiere se recomanda lp/l=0,7 0,8=0,725 sau (l-lp)/l =0,20,3. Valoarea frecvent adoptata in proiectare este: lp/l=0,725, respectiv (l-lp)/l= 0,275.

Figura 3.1.7. Concentrarea masei bielei in doua puncte,
Gb - centrul de greutate
Pozitia centrului de greutate al bielei pentru motoare semirapide si lente, se poate calcula cu formula empirica a lui Terski:
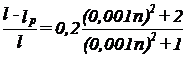 , 27unde n este
turatia nominala a motorului in rot/min.
, 27unde n este
turatia nominala a motorului in rot/min.
Concentrarea masei grupului piston:
Masa grupului piston mp este suma maselor pieselor componente ale pistonului asamblat cu biela:
- motoare cu piston portant
![]() =0,450 kg28
=0,450 kg28
unde: mpiston-masa
pistonului; mbolt-masa boltului pistonului; msegm-masa
tuturor segmentilor montati pe piston. Masa grupului piston nu este
cunoscuta la proiectare si atunci aceasta se determina in
functie de masa relativa ![]() :
:
![]() =8,522*52,8*10-3 =0,45 kg29
=8,522*52,8*10-3 =0,45 kg29
Deoarece grupul piston executa o miscare de translatie, masa acestuia se considera concentrata in punctul B (articulatia bielei cu pistonul).
Adopt masele: ![]() =17,2g/cm2,
=17,2g/cm2,
![]() =9,67 g/cm2,
=9,67 g/cm2,
![]() =8,522 g/cm2.
=8,522 g/cm2.
O estimare mai apropiata de realitate se poate face cu ajutorul motorului ales ca model. Presupunand ca dimensiunile fundamentale (S si D) si configuratiile mecanismelor motoare ale motorului care se proiecteaza sunt suficient de apropiate de cele ale motorului prototip (model) si ca
piesele similare sunt executate din materiale cu aceeasi densitate, atunci intre masele pieselor sau masele concentrate ale celor doua motoare exista relatia:
![]() 30
30
unde: mpr si mmod - masele de acelasi tip (piesa, masa concentrata) ale motorului proiectat si respectiv a motorului model; Dpr si Dmod - diametrele cilindrilor celor doua motoare.
|
Concentrarea masei mecanismului manivela - piston:
Masa mecanismului manivela - piston se considera concentrata in punctele O, A si B, figura 3.1.5. Asa cum s-a aratat, numai masele concentrate in punctele A si B produc forte de inertie:
- masa concentrata in punctul A, mA, (masa in miscare de rotatie in jurul punctului O):
![]() =1,257kg31
=1,257kg31
- masa concentrata in punctul B, mB, (masa in miscare de translatie alternativa de-a lungul axei cilindrului):
![]() =0,14+0,45=0,59 kg
=0,14+0,45=0,59 kg
Fortele de inertie din mecanismul motor:
Masele concentrate produc urmatoarele forte de inertie:
- forta de inertie a masei in
miscare de rotatie, ![]() , produsa de masa mA:
, produsa de masa mA:
![]() =1,257*35,5*10-3*502,642*10-3=11,274
kN32
=1,257*35,5*10-3*502,642*10-3=11,274
kN32
- forta de inertie a masei in
miscare de translatie, ![]() , produsa de masa mB:
, produsa de masa mB:
![]() 33
33
Deoarece forta de inertie FT are modulul variabil in functie de unghiul α, calculul se efectueaza de obicei tabelar ca si la forta de presiune a gazelor.
![]() =0,887*35*502,642*10-6 =7,96 kN
=0,887*35*502,642*10-6 =7,96 kN
![]() =0,370*35,5*502,642*10-6 =3,32 kN
=0,370*35,5*502,642*10-6 =3,32 kN
Fortele care actioneaza in mecanismul motor:
Asupra pistonului actioneaza forta rezultanta F, figura 3.1.8.:
![]() 34
34
In punctul A actioneaza forta de inertie a masei in miscare de rotatie:
![]() 35
35
unde:
![]()

Figura 3.1.8. Fortele care actioneaza in mecanismul motor
36
Deoarece mecanismul manivela - piston are mobilitatea M = 1 apare necesar un moment de echilibrare Me, echivalent cu momentul motor instantaneu rezistent.
Reactiunile din cuplele cinematice:
Pentru fiecare element al mecanismului manivela-piston se pun reactiunile din cuplele cinematice si torsorul fortelor exterioare, figura 3.1.9. a, b, c. Se scriu trei ecuatii de echilibru, doua ecuatii de proiectii de forte dupa axele Ox si Oy si o ecuatie de momente pentru fiecare element si se obtine:
- elementul 3:
![]() 37
37
- elementul 2:
![]() 38
38
- elementul 1:
![]() 39
39
40
unde: β - unghiul de oblicitate al bielei
![]() 41
41
M - momentul motor instantaneu al unui cilindru.

Figura 3.1.9. Reactiunile din cuplele cinematice
ale mecanismului manivela - piston
Reactiunile din cuplele cinematice X01, Y01, X12, Y12, N, si eventual unghiul de oblicitate al bielei β se recomanda sa fie calculate tabelar in functie de unghiul α.
Fortele care actioneaza asupra elementelor mecanismului
Asupra pistonului (elementul 3) actioneaza forta rezultanta F si forta normala N.
Biela (elementul 2) este solicitata de o forta axiala B ce se obtine proiectand reactiunea R32(X32,Y32) pe directia Ax', figura 3.1.10.a. Expresia acestei forte este:
![]() 42
42
Manivela (elementul 1) este solicitata de o forta axial Z si una tangentiala T, reprezentata in figura 3.1.10.b.

![]() 43
43
Figura 3.1.10. Fortele care actioneaza
in elementele mecanismului motor
La manivela mai actioneaza si momentul motor instantaneu:
![]() 44
44
Calculul fortelor B, T, Z si a momentului M se efectueaza tabelar, in functie de unghiul α de rotatie al manivelei.
Momentul motor:
Momentul motor instantaneu M produs de un cilindru al motorului sau al monocilindrului a fost determinat anterior. Momentul motor instantaneu al unui motor policilindric se determina prin insumarea analitica a momentelor motoare instantanee produse de fiecare cilindru, tinand cont de ordinea de aprindere.
Ordinea de aprindere:
Motoarele policilindrice pot avea aprinderile uniforme sau neuniform repartizate. Majoritatea motoarelor au aprinderile uniform repartizate. Se va alege o ordine de aprindere similara cu cea a motorului ales ca model sau de la motoare cu organizare similara. La adoptarea ordinii de aprindere se va tine cont de ordinea de numerotare a cilindrilor in motor si sensul de rotatie al arborelui cotit. S-a ales ordinea: 1-3-4-2.
Perioada momentului motor instantaneu:
Momentul motor instantaneu al intregului motor este o functie periodica. La motoarele cu aprinderi uniform repartizate, perioada φM a momentului motor instantaneu este egala cu decalajul (unghiular) δa al aprinderilor:
![]() ;
;![]() ,45 unde i -
numarul cilindrilor motorului.
,45 unde i -
numarul cilindrilor motorului.
Momentul motor instantaneu al intregului motor:
Se obtine prin insumarea momentelor instantanee produse de fiecare cilindru in conformitate cu ordinea de aprindere:
![]()
unde: Mak - momentul motor instantaneu
dezvoltat in cilindrul k la unghiul ![]() la care se afla
procesul de lucru din cilindrul k fata de cilindrul 1 si se
determina cu relatia:
la care se afla
procesul de lucru din cilindrul k fata de cilindrul 1 si se
determina cu relatia:
![]()
unde: p - ordinul de functii care se obtin
prin permutarea ![]() pe
pe ![]()
o - ordinul de aprindere.
![]()
![]()
![]()

S-a reprezentat in diagrama ![]() - momentul motor
instantaneu al motorului policilindric.
- momentul motor
instantaneu al motorului policilindric.
Momentul motor mediu:
Acesta se calculeaza cu formula:
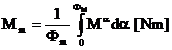
Deoarece nu este cunoscuta expresia
analitica a functiei Ma pentru calculul
momentului mediu se vor aplica metode de integrare numerica. Se va aplica
metoda trapezelor. Intervalul ![]() se imparte in 2n
parti egale. Daca M0, M1, M2,
.,M2n sunt valorile functiilor
se imparte in 2n
parti egale. Daca M0, M1, M2,
.,M2n sunt valorile functiilor ![]() in punctele
respective, atunci:
in punctele
respective, atunci:
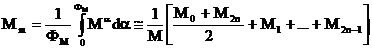 ;
;
![]() 123,28 N·m
123,28 N·m
Calculul puterii efective a motorului:
Fortele care actioneaza in mecanismul motor au fost determinate fara considerarea frecarilor, a rezistentelor mecanismului in general. Puterea efectiva calculata:
![]()
unde: - ![]() 123,28 N·m
123,28 N·m
- ![]() =502,64 rad/s
=502,64 rad/s
- ![]() = randamentul mecanic
al motorului care se adopta egal cu cel al calculului de procese:
= randamentul mecanic
al motorului care se adopta egal cu cel al calculului de procese: ![]()
![]() 66,2 kW
66,2 kW
Intre puterea efectiva calculata Pec si puterea efectiva data prin tema de proiectare trebuie sa existe relatia:
![]() ;
;
Fortele care actioneaza in lagare:
La marea majoritate a constructiilor de motoare, articulatia bielei cu manivela arborelui cotit si rezemarea acestuia in carter se realizeaza prin intermediul unor lagare de alunecare. Pentru a se putea asigura conditiile corespunzatoare de functionare ale acestora, sub aspectul durabilitatii si sigurantei in exploatare, este necesar sa se cunoasca modul in care fortele ce actioneaza in lagare variaza pe circumferinta acestora.
Fortele din lagarul maneton:
Lagarul maneton sau lagarul bielei se compune din cuzinetul de biela si fusul maneton. Fiecare din aceste piese apartin unor elemente diferite, biela si respectiv manivela arborelui cotit. In consecinta, asupra fiecarei componente de lagar actioneaza reactiunea corespunzatoare.
Forta care actioneaza asupra cuzinetului de biela:
1
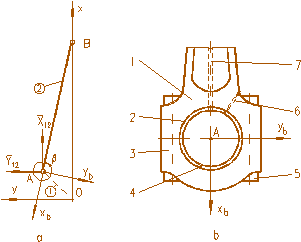
Figura 3.1.11. Fortele care solicita cuzinetul de biela:
a - schema fortelor; b - constructia capului bielei
Forta care actioneaza asupra cuzinetului de biela se obtine prin proiectia reactiunii R12(X12,Y12) pe axele sistemului de referinta xbAyb, fix in raport cu biela, figura 3.1.11.a. Aceasta forta are componentele:
![]() 46
46
Forta care actioneaza asupra fusului maneton
Sistemul de referinta fix in raport cu fusul maneton (manivela sau cotul arborelui cotit) este xmAym, figura 3.1.9.a.
Proiectand reactiunea R21(X21,Y21) pe axele acestui sistem de referinta, se obtin componentele fortei care actioneaza asupra fusului maneton:
![]()
![]()
Diagrama polara a fortei ![]() se reprezinta in
sistem
se reprezinta in
sistem ![]() fix in raport cu fusul
maneton si opus sistemului de referinta
fix in raport cu fusul
maneton si opus sistemului de referinta ![]() .
.
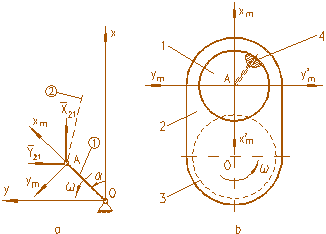
Figura 3.1.12. Fortele care solicita fusul maneton:
a - schema fortelor; b - constructia manivelei arborelui cotit
Pe directia in care, forta cea mai mare ia valoarea minima posibila, se poate practica orificiul canalului de ulei din fusul maneton pentru ungerea lagarului maneton, poz.4, figura 3.1.12.b.
Celelalte pozitii din figura 3.1.12.b au urmatoarele semnificatii:
1 - fusul maneton; 2 - bratul cotului; 3 - fusul palier.
Practicarea canalului trebuie sa fie realizabila tehnologic, ieftina si fara sa afecteze rezistenta la oboseala a cotului arborelui cotit. In caz contrar, se vor analiza alte zone de pe suprafata fusului maneton unde forta are valori relativ reduse.
Verificarea lagarului maneton la soc:
In lagarul maneton actioneaza forta Rb=Rm, care se calculeaza cu relatia:
![]() 47
47
Pentru verificarea presiunii dintre fus si cuzinet si verificarea la incalzire a lagarului maneton, trebuie cunoscuta valoarea medie a fortei din lagarul maneton:
![]() , 48unde φC = τπ este perioada ciclului motor.
, 48unde φC = τπ este perioada ciclului motor.
Gradul de soc cm din lagarul maneton se determina cu formula:
![]()
in care (Rm)max este valoarea maxima a fortei Rm.
Se recomanda ca gradul de soc cm 23.
Calculele pentru componentele fortelor care actioneaza in lagarul maneton Xb, Yb, Xm, Ym si Rm se efectueaza in Excel functie de unghiul α.
Fortele care actioneaza in lagarele paliere extreme:
In figura 3.1.13.a este prezentat primul cot al unui arbore cotit de la un motor cu 'i' cilindri in linie. Arborele cotit are in acest caz c = i coturi. De asemenea, fiecare cot se sprijina in blocul motor prin doua fusuri paliere, numerotate cu 1,2,,i+1. Se considera lagare paliere extreme lagarele cu numerele 1 si i+1. Incarcarea din aceste lagare depinde numai de fortele care actioneaza asupra coturilor extreme 1 si i. La arborii cotiti, la care doua coturi consecutive se sprijina pe doua lagare paliere, incarcarea lagarelor paliere extreme depinde de fortele care actioneaza asupra ambelor coturi.
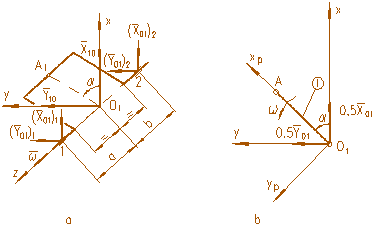
2
Figura 3.1.13. Fortele care actioneaza in lagarul palier extrem
Forta care actioneaza asupra fusului palier extrem:
Se analizeaza cazul cel mai frecvent intalnit si anume cel al arborilor cotiti cu lagar palier dupa fiecare cot.
Asupra cotului extrem, pe axa lagarelor paliere, actioneaza forta R10 la jumatatea distantei dintre bratele extreme. Reactiunile din lagarele paliere 1 si 2, produse de forta R10(X10,Y10), se determina cu relatiile cunoscute:
![]() 49
49
Dimensiunile a si b depind de lungimea fusurilor paliere. Intr-o prima faza se considera
a = b si atunci:
![]() 50
50
Se ataseaza fusului palier extrem (1) sistemul de referinta xpO1xp si care se roteste odata cu manivela (cotul arborelui cotit). Forta care actioneaza asupra fusului palier extrem are componentele:
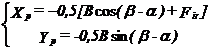
51
Reprezentand fusul palier extrem printr-un cerc suficient de mic in interiorul diagramei polare, se determina zona de incarcare minima in care se poate practica orificiul de ulei. La fel ca si la fusul maneton, practicarea orificiului si a canalului de ulei corespunzator trebuie sa fie realizabila tehnologic si fara sa afecteze rezistenta la oboseala a cotului extrem a arborelui cotit. In caz contrar, se vor lua in considerare alte zone cu incarcare relativ redusa.
Forta care actioneaza asupra cuzinetului palier extrem:

3
Figura 3.1.14. Lagar palier extrem:
a - schema fortelor; b - constructie in varianta 'suspendata'
Cuzinetul lagarului palier extrem este fix in raport cu blocul motor. La motoarele cu lagare paliere in constructie 'suspendata' se adopta sistemul de referinta xcpOycp, figura 3.1.14., iar pentru motoarele cu lagare paliere in constructie 'rezemata' sistemul xO1y. Ambele sisteme de referinta sunt fixe in raport cu blocul motor. Partile componente principale ale unui lagar palier in constructie suspendata, figura 3.1.14.b., sunt: 1- bloc motor; 2 - semicuzinet din bloc;
3 - capac lagar palier; 4 - semicuzinet din capac; 5 - suruburi capac palier; 6 - canal in blocul motor pentru aductiunea uleiului in lagarul palier.
Componentele fortei care solicita cuzinetul palier extrem la motoarele cu lagare paliere in constructie suspendata sunt date de relatiile:
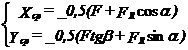 52
52
Fortele care actioneaza in lagarele paliere intermediare:
La majoritatea motoarelor policilindrice, arborele cotit are mai mult de doua fusuri paliere, deci este un sistem static nedeterminat. Calculul exact al fortelor din lagarele paliere este practic imposibil deoarece fusurile paliere sunt montate cu joc in lagare, iar carterul motorului si arborele cotit sunt structuri deformabile.
In consecinta, pentru determinarea fortelor care lucreaza intr-un lagar palier intermediar, se considera cele doua manivele situate de o parte si de alta a fusului palier respectiv. Reactiunea din lagarul palier se obtine prin insumarea vectoriala a reactiunilor produse de fortele care actioneaza asupra coturilor alaturate.
Dupa cum s-a aratat anterior, la motoarele in linie la care fiecare manivela (cot) se sprijina in bloc prin intermediul a doua fusuri paliere, numarul de lagare paliere este i+1. Lagarele paliere 2,3,,i se numesc lagare paliere intermediare. Daca se noteaza cu k numarul de ordine al unei manivele, k=1,2,,i, atunci lagarul palier intermediar k+1 se afla intre manivelele k si k+1.
Se considera ca in lagarul palier intermediar vor produce reactiuni numai fortele care actioneaza asupra manivelelor invecinate, respectiv manivelele k si k+1. Reactiunile se calculeaza asa cum s-a aratat la par. 4.3.2.1., considerand intr-o prima faza ak=bk si ak+1=bk+1.
Forta care actioneaza asupra fusului palier intermediar:
La mijlocul lagarului palier intermediar k+1, in punctul Ok+1, actioneaza reactiunile Xk+1 si Yk+1 produse de manivelele k si k+1, figura 3.15. Aceste reactiuni se determina cu formulele:
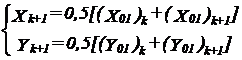 53
53
Componentele fortei care solicita fusul palier intermediar se obtin proiectand reactiunile Xk+1 si Yk+1 pe axele sistemului de coordonate (xpOyp)k+1, fix in raport cu manivela k, figura 3.15.:
 54
54
in care unghiurile αk si αk+1 se determina in functie de ordinea de aprindere.

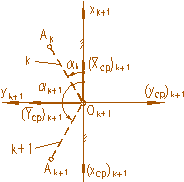
Figura 3.1.16. Schema fortelor care actioneaza asupra cuzinetului palier intermediar k+1
Forta care actioneaza asupra cuzinetului palier intermediar:
La motoarele in linie, componentele fortei care actioneaza asupra cuzinetului lagarului palier intermediar k+1, in sistemul de referinta (xOy)k+1 fix in raport cu blocul motor, sunt:
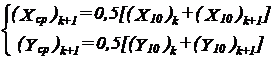
55
In cazul lagarelor in constructie 'suspendata', componentele fortei care solicita cuzinetul
palier intermediar se determina in sistemul de referinta xcpOycp)k+1, fix in raport cu blocul motor si opus sistemului (xOy)k+1. Aceste componente au expresiile:
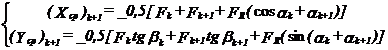
In varianta lagare 'rezemate', componentele (Xcp,Ycp)k+1 au semn schimbat, sistemul de referinta fiind (xOy)k+1.
Se constata ca in expresiile componentelor fortelor care solicita atat lagarele paliere extreme cat si cele intermediare apare forta de inertie a maselor in miscare de rotatie FR. Daca aceste forte sunt echilibrate cu contragreutati montate pe fiecare brat al manivelei, atunci se va considera FR=0.
Verificarea lagarelor paliere la soc:
In lagarele paliere actioneaza forta Rp=Rcp, care se calculeaza cu relatia:
![]() 56
56
Valoarea medie a fortei din lagarul palier:
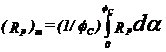 57
57
Gradul de soc cp din lagarul palier se determina cu formula:
![]() 58
58
in care (Rp)max este valoarea maxima a fortei Rp. Se recomanda ca gradul de soc cp 2. In caz contrar se vor revedea calculele de procese in scopul obtinerii unui raport cat mai redus dintre presiunea maxima atinsa in ciclul motor si presiunea indicata.
Calculele pentru componentele fortelor care actioneaza in lagarele paliere extreme si intermediare se recomanda a fi efectuate tabelar, in functie de unghiul α, dupa modelul prezentat la fortele care actioneaza in mecanismul motor.
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||
|
|||
|
|||
Analize pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








