
| Biologie | Botanica | Chimie | Didactica | Fizica | Geografie |
| Gradinita | Literatura | Matematica |
Matematica
|
|
Qdidactic » didactica & scoala » matematica TRANSFORMATA FOURIER - definitia transformatei Fourier, transformata Fourier si diferite operatii, transformata Fourier si convolutia |
TRANSFORMATA FOURIER - definitia transformatei Fourier, transformata Fourier si diferite operatii, transformata Fourier si convolutia
TRANSFORMATA FOURIER
Obiectele fine se obtin prin prelucrari rafinate.
1. Definitia transformatei Fourier
Apeland la seria Fourier (forma complexa)
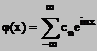 (1)
(1)
realizam
de fapt reprezentarea unei functii periodice ![]() de perioada
de perioada ![]() . Seria Fourier corespunzatoare unei functii de
perioada
. Seria Fourier corespunzatoare unei functii de
perioada ![]() este
este
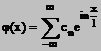 (2)
(2)
Cu formulele uzuale obtinem coeficientii Fourier
![]() (3)
(3)
Din (2) si (3) obtinem
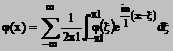 (4)
(4)
Sa observam ca (1)
construieste o functie periodica de perioada ![]() , ca suprapunere de oscilatii armonice pure. Incercand o
trecere la limita dupa 1 cu
, ca suprapunere de oscilatii armonice pure. Incercand o
trecere la limita dupa 1 cu ![]() in (4), gasim o reprezentare a unei functii
definita pe toata axa
in (4), gasim o reprezentare a unei functii
definita pe toata axa ![]() ca suprapunere de
oscilatii armonice.
ca suprapunere de
oscilatii armonice.
Tinand cont de argumentul discret
![]()
se transforma in argumentul continuu
![]() prin trecere la
limita dupa 1, din (4) obtinem
prin trecere la
limita dupa 1, din (4) obtinem
![]() (5)
(5)
numita integrala Fourier a lui ![]() .
.
Notand
![]() (6)
(6)
formula cautata pentru
dezvoltarea lui ![]() in oscilatii armonice simple este
in oscilatii armonice simple este
![]() (7)
(7)
2. Functia ![]() data de (6) se numeste transformata Fourier
a functiei
data de (6) se numeste transformata Fourier
a functiei ![]() , iar (7) se numeste transformata Fourier
inversa. Formulele (6) si (7) au ambele factorul
, iar (7) se numeste transformata Fourier
inversa. Formulele (6) si (7) au ambele factorul ![]() si se mai numesc forme simetrice. Uneori se
opteaza pentru formele nesimetrice.
si se mai numesc forme simetrice. Uneori se
opteaza pentru formele nesimetrice.
![]() (
(![]() )
)
respectiv
![]() (
(![]() )
)
pentru transformata Fourier (![]() ) si inversa sa (
) si inversa sa (![]() ). Dupa factorul din fata este evident cu care
din formule se va lucra.
). Dupa factorul din fata este evident cu care
din formule se va lucra.
3. Transformata Fourier si diferite operatii
In cele ce urmeaza vom nota
operatorul de transformare Fourier cu F si cu ![]() inversul sau.
Deci
inversul sau.
Deci
![]() (*)
(*)
si
![]() (**)
(**)
4. Transformata Fourier si operatia de derivare
Definitie. O functie ![]() se numeste
absolut continua daca
se numeste
absolut continua daca
![]() incat oricare ar fi sistemul finit de intervale disjuncte
incat oricare ar fi sistemul finit de intervale disjuncte ![]() cu
cu
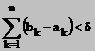 sa avem
sa avem 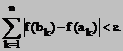
Sa observam ca absolut continuitatea este mai tare ca uniform continuitatea.
|
Sa
presupunem ca ![]() este absolut
integrabila si absolut continua in vecinatatea
oricarui punct si
este absolut
integrabila si absolut continua in vecinatatea
oricarui punct si ![]() este integrabila
pe R.
este integrabila
pe R.
Datorita
integralitatii lui ![]() avem
avem
![]()
Cum 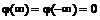 conform celor relatate
anterior, obtinem:
conform celor relatate
anterior, obtinem:
![]() (8)
(8)
Cu alte
cuvinte, derivarii functiei ![]() ii corespunde
inmultirea functiei
ii corespunde
inmultirea functiei ![]() cu
cu ![]() .
.
Daca
![]() are derivate
integrabile pana la ordinul m, atunci repetand (8) obtinem
are derivate
integrabile pana la ordinul m, atunci repetand (8) obtinem
![]() (9)
(9)
5. Transformata Fourier si convolutia
Fie ![]() si
si ![]() transformatele Fourier
ale functiilor absolut integrabile
transformatele Fourier
ale functiilor absolut integrabile ![]() si
si ![]() . Cautam functia care are ca transformata
Fourier produsul
. Cautam functia care are ca transformata
Fourier produsul ![]() ,
, ![]() . Avem
. Avem
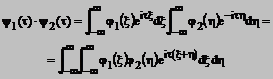
integrala dubla fiind absolut convergenta conform unui rezultat cunoscut al lui Fubinni.
Facand
schimbarea de variabila ![]() pentru a nu avea
doua exponentiale, obtinem
pentru a nu avea
doua exponentiale, obtinem
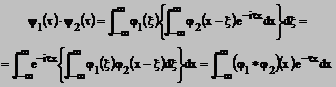
![]()
se numeste convolutia lui ![]() si
si ![]() . Deci produsul
. Deci produsul ![]() provine din
convolutia lui
provine din
convolutia lui ![]() cu
cu ![]() . Deci
. Deci ![]() unde
unde ![]()
6. Ecuatia caldurii rezolvata cu transformata Fourier.
Se cauta solutia deci pentru
![]() (10)
(10)
pentru ![]() si care pentru t = 0 coincide cu
si care pentru t = 0 coincide cu ![]() dat, deci cu
conditia initiala u (x, 0) =
dat, deci cu
conditia initiala u (x, 0) = ![]() . Ca interpretare fizica, problema cere determinarea
temperaturii unei bare infinite omogene si filiforme (deci
unidimensionale) in toate punctele t > 0, daca cunoastem
temperatura sa la momentul initial t = 0.
. Ca interpretare fizica, problema cere determinarea
temperaturii unei bare infinite omogene si filiforme (deci
unidimensionale) in toate punctele t > 0, daca cunoastem
temperatura sa la momentul initial t = 0.
Pentru a ne putea misca liberi in calcule, facem presupuneri suplimentare asupra lui u (t, x) sa le zicem " de a se comporta cuminte".
1. ![]() sunt continue si absolut integrabile in x pentru
sunt continue si absolut integrabile in x pentru ![]() si pentru
si pentru ![]() fixat.
fixat.
2. Functia ![]() admite, pe intreg
intervalul
admite, pe intreg
intervalul ![]() un majorant integrabil
un majorant integrabil
![]()
A aplica
lui (10) transformata Fourier revine la a amplifica cu ![]() si sa integram dupa x de la
si sa integram dupa x de la ![]() la
la ![]() . Dar conform conditiei (11) avem
. Dar conform conditiei (11) avem
![]()
unde
![]()
este transformata Fourier a solutiei cautate u (x, t).
Aplicand formula (2) din c.a., avem
![]()
Am obtinut astfel ecuatia ordinara
![]() (11)
(11)
pentru care trebuie sa cautam solutia care, pentru t = 0, coincide cu:
![]() (12)
(12)
Luand in formula 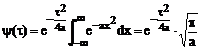 a=1/(4t)
obtinem ca
a=1/(4t)
obtinem ca
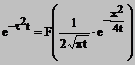 (13)
(13)
Solutia ecuatiei (11) are forma
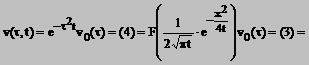
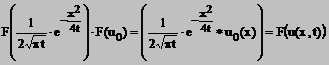
Deci
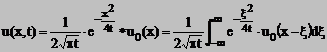 (14)
(14)
Formula obtinuta in (14) se numeste integrala lui Poisson. In teoria ecuatiilor cu derivate partiale, se demonstreaza unicitatea solutiei intr-o vasta clasa de functii nu numai pentru "clasa functiilor cuminti".
Exercitii rezolvate
1.Reprezentati printr-o integrala Fourier functia
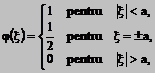
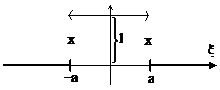
Figura 1
Cu a > 0, functie numita si factorul discontinuu al lui Dirichlet.
Rezolvare Folosind
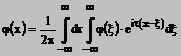 ,
(*)
,
(*)
mai intai calculam
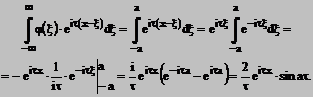
Inlocuind in (*) se obtine
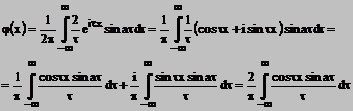
2. Reprezentati printr-o integrala Fourier functia
![]()
Rezolvare conform egalitatii (*) si a functiei date vom scrie
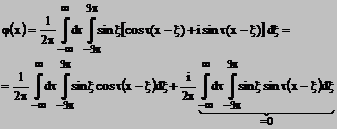
Deoarece ![]() este impara in
raport cu
este impara in
raport cu ![]() ultimul termen din
egalitatile anterioare este nul. Rezulta
ultimul termen din
egalitatile anterioare este nul. Rezulta
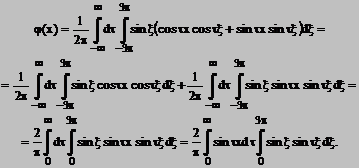
Liniarizand ultimul factor vom obtine
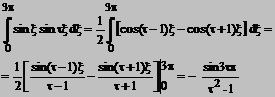
Deci
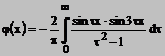
3. Reprezentati printr-o integrala Fourier functia
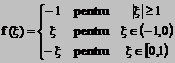
Rezolvare: deoarece 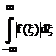 este divergenta,
vom considera functia
este divergenta,
vom considera functia
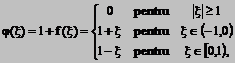
care poate fi reprezentata printr-o integrala Fourier deoarece  este convergenta
si
este convergenta
si ![]() este para conform
graficului.
este para conform
graficului.
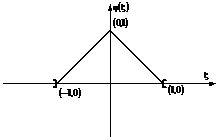
Figura 2
Prin urmare,
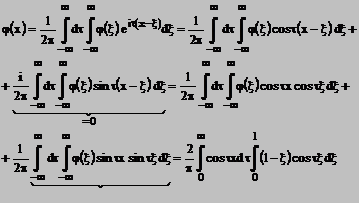
Calcule simple conduc la egalitatea
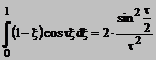
Rezulta
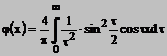
Atunci
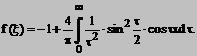
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2026 - Toate drepturile rezervate -| |
|
|
|||
|
|||
|
|||
Referate pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








