
| Biologie | Botanica | Chimie | Didactica | Fizica | Geografie |
| Gradinita | Literatura | Matematica |
Matematica
|
|
Qdidactic » didactica & scoala » matematica Teste grila matematica |
Teste grila matematica
1. Media aritmetica, ca indicator fundamental al tendintei centrale*:
a) reprezinta valoarea care modifica nivelul totalizator al seriei;
b) se foloseste cel mai frecvent si reprezinta suma valorilor raportata la numarul lor;
c) se calculeaza adunand valorile existente;
d) nu poate determina numarul de unitati din colectivitate.
2. Media aritmetica reprezinta*:
a) valoarea pe care ar purta-o fiecare unitate statistica daca distributia ar fi eterogena;
b) valoarea pe care ar purta-o fiecare unitate statistica daca distributia ar fi omogena;
c) valoarea pe care ar purta-o fiecare variabila statistica daca distributia ar fi omogena.
3. Media aritmetica a unei sume dintre doua variabile este egala cu suma mediilor celor doua variabile, cand*:
a) cele doua variabile se afla intr-o relatie de interdependenta;
b) cele doua variabile se afla intr-o relatie de inversa proportionalitate;
c) cele doua variabile se refera la aceeasi colectivitate;
d) cele doua variabile sunt independente;
e) cele doua variabile sunt direct proportionale.
4. Care dintre urmatoarele afirmatii privind media aritmetica este adevarata*:
a) suma patratelor tuturor abaterilor individuale ale termenilor seriei de la media lor aritmetica este zero;
b) marimea mediei aritmetice este cuprinsa intre xmin si xmax doar daca seria prezinta o tendinta clara de asimetrie;
c) pentru o serie de distributie de frecvente, media aritmetica, calculata pe baza frecventelor reduse de c ori, este mai mica decat media seriei initiale de c ori;
d) media produsului a doua variabile aleatoare este egala cu produsul mediilor celor doua variabile;
e) pentru o serie de distributie de frecvente, media calculata pe baza frecventelor relative este egala cu media aritmetica determinata pe baza frecventelor absolute.
5. Mediana, ca indicator statistic:
a) prezinta valoarea din mijlocul unei serii de date in care observatiile au fost ordonate crescator sau descrescator;
b) nu poate fi folosita in caracterizarea tendintei centrale pentru o serie de date masurate pe o scala ordinala;
c) nu are nici o legatura cu notiunea de rang.
6. 25% din salariatii unei inteprinderii au un salariu de cel mult 4 milioane lei. Aceasta valoare reprezinta:
a)quartila unu;
b) mediana;
c) quartila trei.
7. 75% din salariatii unei intreprinderii au un salariu de cel mult 7 milioane lei. Aceasta valoare reprezinta:
a)quartila unu;
b)mediana;
c)quartila trei.
8. 50% din salariatii unei intreprinderii au un salariu de cel mult 5 milioane lei. Aceasta valoare reprezinta:
a)quartila unu;
b)mediana;
c)quartila trei.
9. Intr-o repartitie normala valoarea fata de care 25% din valorile individuale sunt mai mici iar 25% din valorile individuale sunt mai mari este*:
a. cuartila a doua;
b. cuartila a treia;
c. cuartila intai;
d. valoarea modala.
10. Media este o marime generalizata, adica, inlocuind fiecare nivel individual al caracteristicii de distributie cu nivel mediu*:
a. suma termenilor seriei ramane aceeasi;
b. suma termenilor seriei se modifica;
c. suma termenilor seriei este nula.
11. Varianta (dispersia) de grupa masoara*:
a) variatia sub influenta factorilor aleatori (variatia reziduala)
b) variatia sub influenta factorilor esentiali
c) variatia sub influenta factorilor aleatori si esentiali
12. Daca dorim sa obtinem un indicator al tendintei centrale pentru date masurate pe orice scala, vom determina:
a) media aritmetica;
b) modul;
c) media geometrica;
d) media ponderata.
13. Modul se afla dupa relatia:
a) Mo = xi - hMo
*![]() ;
;
b) Mo = xi + hMo
* ![]() ;
;
c) Mo = xi-1 hMo ญญญญญญญญญญญญญญญญญญญญญญญญญญ![]()
14. Care dintre urmatoarele variante nu reprezinta un indicator al tendintei centrale?
a) mod;
b) distributie de frecvente;
c) mediana;
d) medie;
e) medie ponderata.
15. Daca dorim sa obtinem un indicator al tendintei centrale care sa nu fie afectat de valorile extreme, sa poata fi calculat pentru date masurate pe orice scala (cu exceptia celei nominale) si sa aiba o singura valoarea, vom calcula*:
a) media aritmetica
b) modul;
c) media geometrica;
d) mediana;
e) media ponderata.
16. Modul se utilizeaza pentru caracterizarea:
a. tendintei generale si gradului de asimetrie;
b. gradului de boltire;
c. gradului de concentrare.
17. Quartilele sunt marimi de pozitie care impart colectivitatea in:
a. n-1 parti egale;
b. 4 parti egale;
c. 5 parti egale;
18. In distributia de mai jos:
|
Interval |
0 - 5 |
5 - 10 |
10 - 15 |
15 - 20 |
||||
|
ni
|
3 |
7 |
15 |
20 |
Intervalul (15 - 20) reprezinta:
a. intervalul median;
b. intervalul modal;
c. intervalul quartilic.
19. Rolul indicatorilor tendintei centrale ai unei distributii statistice este de a*:
a) sintetiza datele
b) calcula marimile relative
c) aprecia gradul de dispersie al colectivitatii.
20. Asimetria se calculeaza dupa relatia:
a) As=![]() +Mo
+Mo
b) As= 3(![]() -Me)
-Me)
c) As= 2(![]() -Mo)
-Mo)
21. Coeficientul de asimetrie Yule, se calculeaza dupa relatia:
a) Casq= ![]() ; unde: Q1=
Me-Q1
; unde: Q1=
Me-Q1
Q2=Q3-Me
a)
b) Casq= ![]()
b)
c) Casq= ![]()
22. Coeficientul de boltire se calculeaza dupa relatia:
a) β2=![]() c)
β2=
c)
β2= ![]()
b) β2= ![]()
23. O distributie este mezocurtica atunci cand:
a) β2 = 3, γ2 = 0
b) β2 > 3, γ2 >0
c) β2 < 3, γ2 < 0
24. O distributie este leptocurtica atunci cand:
a) β2 = 3, γ2 = 0
b) β2 > 3, γ2 > 0
c) β2 < 3, γ2 < 0
25. O distributie este platicurtica atunci cand:
a) β2 = 3, γ2 = 0
b) β2 > 3, γ2 >0
c) β2 < 3, γ2 < 0
26. Abatarea medie liniara se calculeaza dupa relatia:
a) ![]() c)
c)
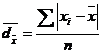
b) 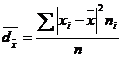
27.
Coeficientul ![]() se utilizeaza
pentru analiza statistica a:
se utilizeaza
pentru analiza statistica a:
a) asimetriei;
b) variatiei;
c) boltirii;
d) tendintei centrale;
e) indicatorilor medii de pozitie.
28. Intr-o serie de repartitie pe intervale formata dupa o anumita variabila, valoarea sa modala este influentata de*:
a) limitele inferioare si superioare ale intervalelor extreme;
b) de frecventele de aparitie ale intervalelor egale sau neegale;
c) de marimea egala sau neegala a intervalelor de variatie;
d) de limita inferioara a intervalului modal;
e) de limita inferioara, de frecventele intervalului modal, premodal si postmodal;
Intrebarile si problemele cu asterix (*) sunt preluate din Jaba E., Pintilescu C., 2005
![]() IV.6. Probleme
IV.6. Probleme
1. Valoarea vanzarilor inregistrate de firma "A" pe parcursul a sapte (7)
zile, se prezinta astfel (in milioane lei) : 200, 250, 750, 1001, 1520, 1800, 2300.
Sa se calculeze valoarea medie zilnica a vanzarilor realizate de firma "A".
2. Distributia dupa volumul vanzarilor zilnice (milioane lei) a unitatilor comerciale dintr-un judet in luna Ianuarie 2004, se prezinta astfel:
|
Volumul vanzarilor |
0 - 10 |
10 - 20 |
20 - 30 |
30 - 40 |
|
Numarul unitatilor comerciale |
50 |
20 |
10 |
5 |
-
Sa se calculeze nivelul mediu al vanzarilor zilnice.
3. Se da urmatoarea distributie:
|
Interval |
ni |
|
10-15 |
5 |
|
15-20 |
10 |
|
20-25 |
12 |
|
25-30 |
6 |
|
30-35 |
8 |
|
35-40 |
4 |
Sa se calculeze modul.
4. O firma inregistreaza, intr-o perioada de 5 zile, urmatoarele date privind volumul vanzarilor (milioane lei) : 5, 7, 20, 14, 9.
- sa se afle valoarea medianei (locul medianei)
5. O firma inregistreaza, intr-o perioada de 6 zile, urmatoarele date privind volumul vanzarilor (milioane lei) : 10, 40, 20, 15, 22, 35.
- sa se afle valoarea medianei .
6. Distributia familiilor dintr-un bloc dupa numarul de copii se prezinta astfel:
|
Numar copii |
Numar familii (ni) |
|
0 |
4 |
|
1 |
8 |
|
2 |
15 |
|
3 |
4 |
|
4 |
2 |
|
5 |
1 |
|
Total |
34 |
Sa se calculeze valoarea medianei.
7. . Distributia muncitorilor unei firme dupa timpul consumat pentru realizarea produsului "A", se prezinta astfel:
|
Timp necesar |
- 30 |
30-60 |
60-90 |
90-120 |
120-15 |
150 - |
|
Numar muncitori |
25 |
50 |
60 |
45 |
15 |
5 |
Sa se calculeze valoarea medianei.
8. Distributia muncitorilor unei firme dupa timpul consumat, pentru realizarea produsului "A" se prezinta astfel:
|
Timpul necesar (minute) x (i-1) ; x (i) |
Numar muncitori Ni |
Xi |
F(ci) |
|
0-30 |
25 |
15 |
25 |
|
30-60 |
50 |
45 |
75 |
|
60-90 |
60 |
75 |
135 |
|
90-120 |
45 |
105 |
180 |
|
120-150 |
15 |
135 |
195 |
|
150-180 |
5 |
165 |
200 |
|
total |
200 |
|
|
Sa se calculeze valoarea quartelei unu.
9. Distributia muncitorilor firmei "A" dupa timpul consumat pentru realizarea produsului"X" se prezinta astfel*:
|
Timp necesar |
- 30 |
30-60 |
60-90 |
90-120 |
120-15 |
150 - |
|
Numar muncitori |
25 |
50 |
60 |
45 |
15 |
5 |
Sa se calculeze valoarea quartilei trei.
10. Distributia unui esantion de firme dupa cifra de afaceri lunara, X, in mil lei, in anul 2004, este prezentata astfel*:
|
Xi-1; Xi |
ni |
|
176-178 |
20 |
|
178-180 |
25 |
|
180-182 |
40 |
|
182-184 |
35 |
|
184-186 |
30 |
|
186-188 |
10 |
|
Total |
160 |
Sa se calculeze abaterea medie liniara.
11. . Daca: Q1= 128,13 mil. lei
Me= 137,86 mil. lei
Q3= 147,92 mil. lei
Atunci, coeficientul de asimetrie Yule este egal cu*:
a) 141 si arata o distributie simetrica
b) 0, 016 si arata o distributie moderat asimetrica
c) 0,016 si arata o distributie puternic asimetrica.
12. Pentru o distributie s-au stabilit urmatoarele rezultate*:
Q1= 150
Me= 130
Q3=140.
Sa se calculeze valoarea coeficientului de asimetrie Yule.
13. Pentru o distributie s-au obtinut urmatoarele rezultate*:
m4 = 40.000 ;m2 = 100.
Sa se calculeze valoarea coeficientului de boltire.
14. Daca:m4 = 54059,44
m2 = 162,6
atunci coeficientul de boltire si interpretarea sa corecta sunt:
a) β = 2,045 → arata o distributie usor platicurtica;
b) β = 2,045 → arata o distributie usor leptocurtica;
c) β = 2,045 → arata o distributie usor mezocurtica.
15. Pentru o distributie s-au obtinut urmatoarele rezultate*:
Mo = 125 minute
![]() = 130 minute
= 130 minute
![]() = 12 minute.
= 12 minute.
Sa se calculeze valoarea coeficientului empiric de asimetrie Pearson.
16. Distributia unui esantion de firme dupa cifra de afaceri lunara X, in milioane lei, in anul 2004, este:
|
Interval |
176-178 |
178-180 |
180-182 |
182-184 |
184-186 |
186-188 |
|
ni |
20 |
25 |
40 |
35 |
30 |
10 |
Sa se calculeze variatia (dispersia).
17. Pentru o distributie statistica s-a obtinut o valoare a coeficientului de boltire egala cu 2,5*.
Sa se calculeze coeficientul Fisher.
![]()
18. Distributia unui esantion de firme dupa cifra de afaceri lunara, X, in mil. lei, in anul 2006, este:
|
Interval |
176-178 |
178-180 |
180-182 |
182-184 |
184-186 |
186-188 |
|
ni |
20 |
25 |
40 |
35 |
30 |
10 |
Sa se calculeze valoarea coeficientului de variatie.
Intrebarile si problemele cu asterix (*) sunt preluate din Jaba E., Pintilescu C., 2005
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2026 - Toate drepturile rezervate -| |
|
|
|||
|
|||
|
|||
Referate pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








