
| Biologie | Botanica | Chimie | Didactica | Fizica | Geografie |
| Gradinita | Literatura | Matematica |
Statistica
|
|
Qdidactic » didactica & scoala » matematica » statistica Repartitii teoretice importante - repartitia binomiala - forma limita si generala |
Repartitii teoretice importante - repartitia binomiala - forma limita si generala
Repartitia binomiala
Legea binomiala permite descrierea probabilitatilor asociate cu privire la doua experimente exclusive.
Pentru evitarea unor exemple particulare (monede, zaruri), vom folosi termenul de ‘succes’ pentru aparitia unui eveniment (probabilitatea_1=p) si ‘insucces’ pentru neaparitia sa (probabilitatea_2=q). Evident vom avea p+q=1.
Consideram ca toate evenimentele intr-un numar de incercari sunt independente, adica probabilitatile p si q sunt aceleasi pentru fiecare eveniment si raman constante de-a lungul incercarilor.
Presupunem ca efectuam un numar de N serii in care efectuam cate n incercari in fiecare din cele N serii si determinam numarul de succese din fiecare serie (ex. Aruncam o moneda de 10 ori pentru fiecare serie, observand de cate ori apare stema la fiecare serie).
In general, vor exista unele serii la care nu vom observa succese, altele la care vom observa un succes, altele cu doua succese s.a.m.d. Prin urmare daca grupam seriile in raport cu numarul de succese vom obtine o repartitie de frecventa.
Ex. 12 zaruri aruncate de 4096 de ori, aparitia lui 6 fiind considerata un succes, conduce la urmatorul rezultat.
Nr. succese 0 1 2 3 4 5 6 7 si mai mult.
Nr. aruncari 447 1145 1181 796 380 115 24 8
Vom arata ca, folosind ipotezele de independenta a experientelor succesive vom putea determina teoretic natura acestei repartitii.
In cazul seriilor cu o singura incercare, estimam ca in N astfel de serii sa obtinem Np succese si Nq insuccese.
Cand avem doua incercari, posibilitatile sunt:
SS SI IS II
p2+2pq+q2 de N ori
Cand avem trei incercari:
SSS SSI ISS IIS ISI SII III
Deoarece nu conteaza ordinea in care au aparut succesele si insuccesele, putem scrie
SSS 3SSI 3SII III
p3 + 3p2q + 3pq2 + q3 sau
p3 + C31p2q + C32pq2+q3
Pentru n incercari, obtinem formula generala (dezvoltarea binomiala):
N
Exmplul1.Daca luam 100 de serii cu cate10 aruncari ale unei monezi perfecte, in cate cazuri ne asteptam sa obtinem de 7 ori stema si de 3 ori valoarea?
R. Aici avem p=![]() , q=
, q=![]() .
.
Frecventele a celor 0,1,,10 succese sunt termenii din dezvoltarea binomiala,
![]() Termenul care
da frecventa a 7 succese si a 3 insuccese este:
Termenul care
da frecventa a 7 succese si a 3 insuccese este:
|
![]()
E Exmplul 2. Acelasi text cu intrebarea: in cate cazuri ne asteptam sa obtinem cel putin de 7 ori stema.
R. Cautam suma termenilor corespunzatori la 7,8,9 si 10 succese:
![]()
Forma generala a repartitiei binomiala depinde de valorile lui p si q si de valorile exponentului n (numarul de incercari din fiecare serie).
Daca p si q sunt egali, repartitia este evident simetrica, deoarece p si q pot fi permutati intre ei, fara a schimba valoarea vreunui termen si prin urmare termenii echidistanti de la cele doua capete ale seriei sunt egali. Daca p si q nu sunt egali, repartitia este asimetrica.
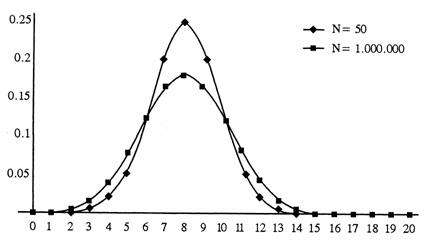
Forma limita a repartitiei binomiala. Cand n creste, fiecare termen al repartitiei binomiala scade. Insa suma unor termeni care cad intre anumite limite nu va fi mica.
Chiar daca p nu este egal cu q, cand n devine din ce in ce mai mare, repartitia binomiala tinde catre forma unei curbe continue simetrice. In figura de mai jos am exemplificat (Yule, Kendal, 1969) tendinta spre simetrie pe care o are repartitia binomiala (0,9+0,1)n pentru diferite valori ale lui n.
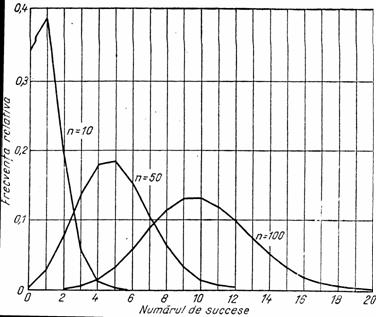
Se demonstreaza ca valoarea maxima este atinsa intr-un anumit punct pe care il vom nota cu pk si care este data de
![]()
Astfel functia care aproximeaza foarte bine valorile repartitiei binomiale este
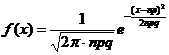
unde
np= valoarea mediei
![]() =
= ![]() = abaterea medie
patratica
= abaterea medie
patratica
Astfel la modul general putem scrie functia sub forma
![]()
Aceasta functie se numeste curba normala. De parametri m si s si se noteaza N(m,s). Reprezentarea grafica a acestei distributii este o curba in forma de clopot simetrica fata de axa Oy si a carei forme este determinata de valoarea lui s. Aceasta curba mai este numita si curba lui Gauss. In figura de mai jos sunt prezentate doua curbe normale pentru diferite valori ale lui m si s
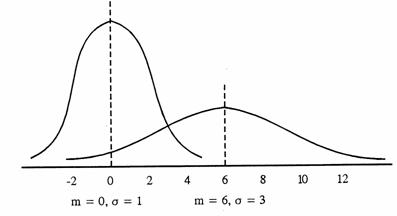
Proprietati ale curbei normale
Curba
normala este simetrica in jurul punctului x=0, in acest punct
isi atinge valoarea maxima. Curba normala este complet
specificata daca se defineste media (originea lui x),
abaterea standard ![]() si valoarea
si valoarea ![]() . In practica, daca dorim sa obtinem o
curba normala cu ajutorul unor date cunoscute, valoarea lui
. In practica, daca dorim sa obtinem o
curba normala cu ajutorul unor date cunoscute, valoarea lui ![]() nu se da direct,
ci se calculeaza folosind faptul ca aria curbei trebuie sa fie
egala pe scala aleasa, cu numarul total de observatii.
nu se da direct,
ci se calculeaza folosind faptul ca aria curbei trebuie sa fie
egala pe scala aleasa, cu numarul total de observatii.
Aria determinata de curba normala si axa Ox este:
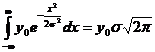
Daca luam ![]() , aria este egala cu unitatea.
, aria este egala cu unitatea.
In aceasta situatie putem obtine imediat forma corespunzatoare unei repartitii de orice frecventa data. Astfel, daca frecventa este N, curba normala corespunzatoare este:
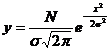 .
.
Media curbei normale, asa cum am vazut, este localizata in origine. Daca dorim sa scriem expresia curbei, in raport cu un alt punct ca origine, obtinem forma:
![]()
![]()
Unde m este abaterea de la medie a valorii alese ca origine.
![]() este dispersia;
este dispersia;
![]() este abaterea medie patratica
(abaterea standard).
este abaterea medie patratica
(abaterea standard).
Proprietatile curbei normale
Curba normala este evident simetrica in jurul punctului x=0, deoarece ecuatia ei este independenta de semnul lui x. In acest punct ordonata isi atinge valoarea maxima. Valoarea medie, mediana si modulul coincid. Este considerata o curba simetrica ideala.
Curba normala este complet
specificata daca se defineste media (originea lui x),
abaterea medie patratica ![]() si valoarea
si valoarea ![]() . In
practica, daca dorim sa obtinem o curba normala
cu ajutorul unor date cunoscute, valoarea lui
. In
practica, daca dorim sa obtinem o curba normala
cu ajutorul unor date cunoscute, valoarea lui ![]() nu se da direct, ci se calculeaza
folosind faptul ca aria curbei trebuie sa fie egala, pe scara
aleasa, cu numarul total de observatii.
nu se da direct, ci se calculeaza
folosind faptul ca aria curbei trebuie sa fie egala, pe scara
aleasa, cu numarul total de observatii.
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||
|
|||
|
|||
Proiecte pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








