
| Biologie | Botanica | Chimie | Didactica | Fizica | Geografie |
| Gradinita | Literatura | Matematica |
Matematica
|
|
Qdidactic » didactica & scoala » matematica Inele si corpuri |
Inele si corpuri
Inele si corpuri
Definitie. O
multime nevida ![]() , luata impreuna cu doua legi de
compozitie
, luata impreuna cu doua legi de
compozitie
![]()
si
![]()
se numeste inel daca :
![]() este grup abelian,
este grup abelian,
![]() este monoid,
este monoid,
![]() Distributivitatea :
Distributivitatea : ![]()
![]() .
.
Daca a doua operatie a inelului satisface si axioma :
![]()
spunem ca A este inel comutativ.
Definitie. Fie ![]() un inel,
un inel, ![]() elementul neutru in
raport cu prima operatie. Spunem ca
elementul neutru in
raport cu prima operatie. Spunem ca ![]() este inel fara divizori ai lui zero
daca
este inel fara divizori ai lui zero
daca ![]() si
si ![]() . Un inel comutativ, cu cel putin doua elemente
si fara divizori ai lui zero se numeste domeniu
de integritate.
. Un inel comutativ, cu cel putin doua elemente
si fara divizori ai lui zero se numeste domeniu
de integritate.
Definitie. Fie ![]() si
si ![]() doua inele
si
doua inele
si ![]() . Aplicatia
. Aplicatia ![]() se numeste izomorfism
de inele, daca :
se numeste izomorfism
de inele, daca :
i. ![]() este functie
bijectiva
este functie
bijectiva
ii. ![]() este morfism
de inele, adica :
este morfism
de inele, adica :  pentru
pentru ![]() .
.
Definitie. Un inel ![]() se numeste corp
daca elementele neutre ale celor doua legi sunt diferite si
orice element
se numeste corp
daca elementele neutre ale celor doua legi sunt diferite si
orice element ![]() , diferit de elementul neutru al primei legi este
simetrizabil in raport cu cea de a doua lege.
, diferit de elementul neutru al primei legi este
simetrizabil in raport cu cea de a doua lege.
Un corp se numeste comutativ daca a doua lege este comutativa.
Aplicatii BAC 2009
1. Se considera multimea de matrice 
a). Sa se arate ca, daca ![]() , atunci
, atunci ![]()
b). Sa se arate ca, daca ![]() si
si ![]() , atunci
, atunci ![]() sau
sau ![]()
c). Admitem cunoscut faptul ca ![]() este inel in raport cu
adunarea si inmultirea matricelor. Sa se determine elementele
inversabile ale acestui inel.
este inel in raport cu
adunarea si inmultirea matricelor. Sa se determine elementele
inversabile ale acestui inel.
2. Fie inelul ![]()
a). Sa se dea exemplu de un numar complex ![]() astfel incat
astfel incat ![]() si
si ![]()
|
b). Sa se determine elementele inversabile ale
inelului ![]()
c). Sa se arate ca multimea ![]() este parte
stabila a lui
este parte
stabila a lui ![]() in raport cu
inmultirea.
in raport cu
inmultirea.
3. Se considera inelele ![]() si
si ![]() .
.
a). Sa se arate ca, daca ![]() si
si ![]() , atunci
, atunci ![]()
b). Sa se arate ca ![]()
c). Sa se arate ca nu exista morfisme de
inele de la ![]() la
la ![]()
4. Se considera cunoscut ca ![]() este un inel
comutativ, unde
este un inel
comutativ, unde ![]() si
si ![]() ,
, ![]() .
.
a). Sa se arate ca elementul neutru al legii "![]() " este 4.
" este 4.
b). Sa se determine ![]() astfel incat intre
inelele
astfel incat intre
inelele ![]() si
si ![]() sa existe un
izomorfism de forma
sa existe un
izomorfism de forma ![]() ,
, ![]() .
.
c). Sa se rezolve in multimea ![]() ecuatia
ecuatia ![]() .
.
Inelul claselor de resturi modulo ![]()
5. Fie ![]() inelul claselor de
resturi modulo 21.
inelul claselor de
resturi modulo 21.
a). Sa se arate ca suma elementelor inelului
este ![]() .
.
b). Sa se calculeze ![]() .
.
c). Sa se determine numarul elementelor neinversabile ale inelului.
6. Se considera corpul ![]() si
si ![]() .
.
a). Sa se arate ca ![]() .
.
b). Sa se arate ca, pentru orice ![]() exista
exista ![]() astfel incat
astfel incat ![]() .
.
c). Sa se arate ca ![]() .
.
7. Se considera multimile de clase de resturi ![]() si
si ![]() .
.
a). Sa se rezolve in corpul ![]() ecuatia
ecuatia ![]() .
.
b). Sa se determine ordinul elementului ![]() in grupul
in grupul ![]() .
.
c). Sa se arate ca nu exista niciun morfism
de grupuri ![]() cu
cu ![]() .
.
8. Se considera multimea 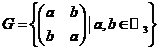 .
.
a). Sa se determine numarul elementelor
multimii ![]() .
.
b). Sa se arate ca ![]() , pentru orice
, pentru orice ![]() .
.
c). Sa se determine numarul matricelor din
multimea ![]() care au determinantul
nul.
care au determinantul
nul.
9.Se considera multimea  .
.
a). Sa se determine numarul elementelor
multimii ![]() .
.
b). Sa se dea exemplu de matrice ![]() cu proprietatea
ca
cu proprietatea
ca ![]() si
si ![]() .
.
c). Sa se determine numarul solutiilor
ecuatiei  ,
, ![]() .
.
10. Se considera multimea ![]() , submultimea
, submultimea  si matricele
si matricele  si
si  .
.
a). Sa se verifice ca daca ![]() , atunci
, atunci ![]() daca si
numai daca
daca si
numai daca ![]() .
.
b). Sa se arate ca multimea ![]() este un subgrup al
grupului multiplicativ al matricelor inversabile din
este un subgrup al
grupului multiplicativ al matricelor inversabile din ![]() .
.
c). Sa se rezolve ecuatia ![]() , unde
, unde ![]() .
.
11. Se considera inelul ![]() unde
unde 
a). Sa se determine numarul elementelor
multimii ![]()
b). Sa se rezolve in multimea ![]() ecuatia
ecuatia ![]()
c). Sa se arate ca ![]() nu este corp.
nu este corp.
12. Se considera multimea  .
.
a). Sa se determine numarul elementelor
multimii ![]() .
.
b). Sa se arate ca ![]() , pentru orice
, pentru orice ![]() .
.
c). Sa se arate ca ![]() este un grup, unde "
este un grup, unde "![]() " este inmultirea mtricelor.
" este inmultirea mtricelor.
13. Se considera multimea  .
.
a). Sa se verifice ca daca  si
si  , atunci
, atunci ![]() .
.
b). Sa se arate ca ![]() este un grup cu 10
elemente.
este un grup cu 10
elemente.
b). Sa se determine numarul elementelor de
ordinul 2 din grupul ![]() .
.
14. Se considera multimea de matrice  .
.
a). Sa se determine numarul elementelor
multimii ![]() .
.
b). Sa se arate ca, pentru orice ![]() ,
, ![]() sau
sau ![]() .
.
c). Sa se determine numarul matricelor ![]() din multimea
din multimea ![]() cu proprietatea
cu proprietatea ![]() .
.
15. Se considera multimea  .
.
a). Sa se determine numarul elementelor
multimii ![]() .
.
b). Sa se arate ca ![]() este parte
stabila in raport cu inmultirea matricelor din
este parte
stabila in raport cu inmultirea matricelor din ![]()
c). Sa se rezolve ecuatia ![]() , cu
, cu ![]() .
.
16. Fie multimea de matrice 
a). Sa se dea un exemplu de o matrice nenula din
multimea ![]() care are determinantul
care are determinantul
![]() .
.
b). Sa se arate ca exista o matrice
nenula ![]() astfel incat
astfel incat 
c). Sa se rezolve ecuatia 
17. Fie multimile ![]() si
si  .
.
a). Sa se determine elementele mutimii ![]() .
.
b). Fie ![]() astfel incat
astfel incat ![]() . Sa se arate ca
. Sa se arate ca ![]() .
.
c). Sa se arate ca ![]() este grup abelian in
raport cu operatia de inmultire a matricelor.
este grup abelian in
raport cu operatia de inmultire a matricelor.
18. Se
considera multimea  .
.
a). Sa se determine numarul de elemente al
multimii ![]() .
.
b). Sa se arate ca ![]() este un grup in raport
cu operatia de inmultire a matricelor din
este un grup in raport
cu operatia de inmultire a matricelor din ![]() .
.
c). Sa se arate ca ![]() , oricare ar fi
, oricare ar fi ![]() .
.
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2026 - Toate drepturile rezervate -| |
|
|
|||
|
|||
|
|||
Lucrari pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








