
| Biologie | Botanica | Chimie | Didactica | Fizica | Geografie |
| Gradinita | Literatura | Matematica |
Gramatica
|
|
Qdidactic » didactica & scoala » literatura » gramatica Rezistenta grinzilor in prezenta fortei taietoare |
Rezistenta grinzilor in prezenta fortei taietoare
REZISTENTA GRINZILOR IN PREZENTA FORTEI TAIETOARE
1. Eforturi unitare tangentiale. Formula lui Juravski
Se considera volumul ABCD, decupat din bara (fig.3.57). Echilibrul de translatii pe directia axului barei (fig.3.58) este asigurat de fortele de interactiune a caror masura, pe sectiunea transversala este sistemul eforturilor unitare s, iar pe sectiunea longitudinala - forta elementelor de lunecare
dL = bdz (3.37)

Fig. 3.57

Fig. 3.58
In prezenta unor momente incovoietoare pozitive, la partea superioara a barei, eforturile unitare t masoara compresiuni. Pe cele doua sectiuni transversale compresiunile sunt diferite, caci in prezenta fortei taietoare momentul incovoietor variaza. Cresterea de a rezultantei volumului de compresiuni este echilibrata de forta elementara de lunecare dL:
dL = dC (3.38)
Rezultanta volumului de compresiune cu expresia
C = SA, sdA
unde A’ este aria sectiunii transversale aflate in interactiune, inlocuind efortul s cu expresia (3.18), se obtine
C = SA’ ![]() ,
,
C = ![]()
unde S’x este momentul static al suprafetei partiale A’ a sectiunii transversale in raport cu axa x; de aici
dC = dMx ![]() (3.39)
(3.39)
Din (3.37), (3.38) si (3.39) rezulta
bdz = dMx ![]()
= ![]()
si
= ![]() (3.40)
(3.40)
In expresia (3.40), care poarta numele lui Juravski, s reprezinta efortul unitar tangential yz din planul longitudinal egal cu efortul unitar tangential zy din planul sectiunii transversale; ambele planuri trec prin punctul C in care ne-am propus determinarea efectului fortei taietoare (fig. 3.57 si 3.58). Semnificatia parametrilor din membrul drept al formulei lui Juravski este urmatoarea:
T - forta taietoare din sectiune;
S’x - momentul static in raport cu axa x (axa neutra a sectiunii) al suprafetei partiale A’ determinate pe sectiunea transversala de planul longitudinal ce trece prin punctul C (punctul in dreptul caruia se defineste efortul tangential); momentul static al suprafetei A’ este egal cu momentul static al suprafetei” (S’x + S”x = Sx = 0, caci Sx reprezinta momentul static al unei suprafete in raport cu o axa ce trece prin centrul de greutate; in valoare absoluta, S’x = S”x);
b - latimea sectiunii transversale in dreptul punctului considerat;
Ix - momentul de inertie al suprafetei sectiunii in raport cu axa x (axa neutra a sectiunii).

Fig. 3.58
2.1. Distributia eforturilor unitare pe sectiunea transversala; eforturi unitare tangentiale maxime. Asa cum rezulta din formula lui Juravski, parametrii care determina variatia eforturilor unitare … pe sectiunea transversala sunt b si S. La sectiunile dreptunghiulare (cu latime constanta), variatia eforturilor este determinata doar de variatia momentului static. Expresia momentului static, in functie de cota y a planului de lunecare, este (fig.3.59):
|
S(y)
= b (
Ei - si deci si efortului unitar - ii corespunde o variatie parabolica, simetrica in raport cu axa x, cu valori nule pentru y = h/2 (la extremitatile sectiunii) si valoarea

Fig. 3.59
maxima pentru y = 0 (in dreptul axei x, axa neutra a sectiunii).
Pentru y = 0
Smax = ![]()
tmax = ![]()
tmax = 1,5 ![]() = 1,5 t med (3.41)
= 1,5 t med (3.41)
unde s med s-a notat efortul unitar (fictiv) corespunzator unei distributii uniforme pe sectiunea transversala.
La sectiunile de tip I si asimilate, cu sectiunea talpilor si a inimii de forma dreptunghiulara, distributia eforturilor unitare este cea din fig.3.60.a. Variatia parabolica este intrerupta de salturi in dreptul modificarii bruste a latimii sectiunii.

Fig. 3.60 Fig. 3.61
In realitate aceasta variatie brusca a formei este sursa unor perturbatii in distributia teoretica a eforturilor unitare si generaeza concentraii de eforturi (fig.3.60.b). Pentru atenuarea varfului de efort, sectiunile profilelor laminate de acest tip au laturile unite prin racordari (fig. 3.61).
2.2. Verificarea rezistentei la forfecare. La grinzi cu sectiune de forma dreptunghiulara eforturile unitare tangentiale sunt mici in comparatie cu eforturile unitare normale. Aplicatia din fig.3.ba este edificatoare.
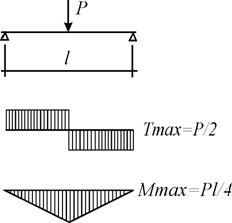
Fig. 3.62
smax = 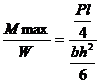
max = 1,5 
de unde
![]()
Se vede ca pentru grinzi cu proportie normala, raportul max este net in favoarea efortului unitar t; de aceea aceste grinzi se verifica numai la incovoiere.
In mod curent verificarea la forfecare nu este necesara nici in cazul grinzilor cu sectiune I sau asimilata acesteia, desi eforturile unitare tangentiale sunt mai mari ca cele corespunzatoare sectiunii dreptunghiulare.
3. Rezistenta barelor in sectiuni longitudinale (rezistenta la lunecare)
3.1. Determinarea fortei de lunecare. Variatia fortei de lunecare
Observatie privind ipteza lui Bernoulli. Forta elementara de lunecare a fost determinata in paragraful 1.
dL = dM![]()
Pe lungimea finita cuprinsa intre doua sectiuni (A si B),
LAB = ![]()
LAB = 
LAB = ![]() AT (3.42)
AT (3.42)
unde AT este aria diagramei de forte taietoare cuprinsa intre sectiunile A si B.
La grinzile cu sectiune constanta (cazul curent), forta de lunecare este proportionala cu aria diagramei de forte taietoare, deci maxima spre reazemele grinzii.
In planuri situate la cote diferite, forta de lunecare este proportionala cu momentul static, deci maxima in dreptul planului neutru. In fig.3.b se exprima aceasta variatii prin deplasari relative diferite intre fasii longitudinale de bara.
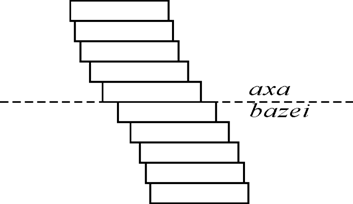
Fig. 3.63
Imaginea obtinuta infirma ipoteza lui Bernoulli (a sectiunilor plane….).
Tipul de deformatie din fig.3.b3 este doar una din cele trei componente ale deformatii complexe cu care bara raspunde solicitarii de incovoiere cu forte taietoare; ele sunt prezentate in fig.3.64.

Fig. 3.64
3.2. Probleme practice privind asigurarea interactiunii longitudinale. Cand dimensiunile prea mari ale sectiunii transversale nu permit realizarea grinzii dintr-o singura bucata, in planurile longitudinale care separa elementele componente ale grinzii se manifesta tendinte de lunecare (fig.3.65). In cele ce urmeaza se prezinta

Fig. 3.65
modul particular de blocare a acestor lunecari (asigurarea interactiunii longitudinale) la diferite tipuri de astfel de grinzi.
I. Grinzi de lemn cu sectiune compusa
La acest tip de grinda asigurarea interactiunii longitudinale se realizeaza, traditional, prin intermediul penelor (fig.3.66). Distanta dintre pene depinde de capacitatea lor la forfecare si de marimea de capacitatea lor la forfecare si de marimea fortelor de lunecare.
La grinzile de mare deschidere sau in cazul in care forta taietoare prezinta variatii mari in lungul grinzii, se urmareste ca prin asezarea penelor la distante diferite (mici in zonele cu forta taietoare mare, deci lunecari puternice si mari zonele cu forta taietoare redusa) sa se realizeze o incarcare uniforma a penelor.

fig. 3.66
Istoria constructiilor si sistemul din fig. 3.68, marcabil prin eleganta solutiei.
![]()
fig. 3.68
II. Grinzi metalice cu sectiune compusa de tip I sau asimilata. Asigurarea in turatiuni longitudinale intre inima si talpi - elementele componente ale grinzii - se realizeaza prin imbinari sudate (fig.3.69) sau nituite (3.70)

fig. 3.69

fig. 3.70
III. Grinzi cu zabrele. Lunecarea dintre cele doua talpi este blocata de legaturi de tip pendul, asigurate de bare transversale simple, articulate la capete, compuse in sistem cu ochiuri triunghiulare (fig. 3.71 si 3.72)

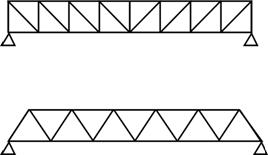
Fig. 3.71 Fig. 3.72
Barele transversale (denumite, in functie de orientarea lor, diagonale sau montanti) sunt alternativ comprimate si intinse (pentru sensul tendintei de lunecare precizat in fig.3.71, diagonala din stanga este comprimata, iar cea din dreapta intinsa).
IV. Grinzi Vierendel. Lunecarea dintre cele doua talpi este blocata de montanti robusti, incastrati la capete, formand, impreuna cu talpile, sisteme cu ochiuri dreptunghiulare (fig.3.73 si 3.74). Montantii sunt forfecati si incovoiati.

Fig. 3.73 Fig. 3.74
 V. Grinda de beton armat. Grinda de beton armat (fig.3.75
si 3.76) poate fi asimilata cu o grinda cu zabrele: talpa
superioara (comprimata) este alcatuita din beton simplu
(doar pe cca un sfert din inaltimea sa grinda de beton armat este
comprimata), talpa inferioara (intinsa) este alcatuita
din bare longitudinale de otel (armaturi) iar elementele transversale
“de coasere” ale celor doua talpi - din “vine” de beton comprimat
si armaturi intinse (in doua variante: bare inclinate, de tip
diagonale si etrieri, de tip montanti).
V. Grinda de beton armat. Grinda de beton armat (fig.3.75
si 3.76) poate fi asimilata cu o grinda cu zabrele: talpa
superioara (comprimata) este alcatuita din beton simplu
(doar pe cca un sfert din inaltimea sa grinda de beton armat este
comprimata), talpa inferioara (intinsa) este alcatuita
din bare longitudinale de otel (armaturi) iar elementele transversale
“de coasere” ale celor doua talpi - din “vine” de beton comprimat
si armaturi intinse (in doua variante: bare inclinate, de tip
diagonale si etrieri, de tip montanti).

Fig. 3.75 Fig. 3.76
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
 |
|||
|
|||
|
|||
Proiecte pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








