
Management
Metode de fundamentare a deciziilor
Metode de fundamentare a deciziilor
Asigurarea unui management dinamic, pe
baze stiintifice, necesita exprimarea diferitelor fenomene sau
fapte prin intermediul teoriilor si tehnicilor matematice, utilizarea
legitatilor sau relatiilor functionale pentru construirea
diferitelor modele, experimentarea pe aceste modele a unor strategii posibile
si stabilirea unui astfel de sistem de planificare, evidenta
si analiza economica care sa permita adoptarea in
orice moment a unor alternative de actiune optime, care sa asigure o
crestere continua a rentabilitatii intreprinderii.
Metodele de optimizare a deciziilor se
pot clasifica in functie de caracterul unicriterial sau multicriterial al
procesului decizional si in functie de incadrarea acestuia in
conditii de risc sau incertitudine. Astfel, pentru conditii de risc
se aplica teoria probabilitatii, pentru conditii de
incertitudine se aplica teoria jocurilor,iar pentru decizii
multicriteriale, se aplica teoria utilitatii. In
numeroase cazuri, pentru solutionarea problemelor complexe in care
intervin o multime de factori aleatori, se utilizeaza simularea
economica. De asemenea, o categorie importanta de probleme decizionale
se pot solutiona cu ajutorul tehnicilor matematice ale cercetarilor
operationale.
1. Teoria probabilitatii
Aceasta metoda se aplica
pentru fundamentarea deciziilor unicriteriale in conditii de risc, cand
alternativele posibile de actiune sunt afectate de o serie de evenimente
aleatoare, determinand astfel o variatie probabilistica a
rezultatelor economice estimate a se obtine. Pentru aplicarea acestei
metode se utilizeaza o matrice decizionala (tab. 3.2).
Tabel 3.2. Matrice decizionala
|
S1
(p1)
|
.Sj
(pj)
|
.Sk
(pk)
|
|
VD1
|
R11
|
.R1j
|
.R1k
|
|
VDi
|
Ri1
|
.Rij
|
.Rik
|
|
VDm
|
Rm1
|
.Rmj
|
.Rmk
|
unde: Rij , i = 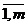 , j =
, j =  reprezinta rezultatul
estimat a se obtine daca se aplica varianta decizionala VDi,
in conditiile in care apare starea Sj, cu probabilitatea pj
, astfel incat
reprezinta rezultatul
estimat a se obtine daca se aplica varianta decizionala VDi,
in conditiile in care apare starea Sj, cu probabilitatea pj
, astfel incat  = 1.
= 1.
Pentru fiecare varianta
decizionala VDi se calculeaza valoarea medie
asteptata a rezultatelor probabile, cu relatia (3.1).
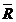 (VDi) =
(VDi) = 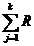 ij ∙ pj (3.1)
ij ∙ pj (3.1)
Selectia alternativei optime se
face cu relatia (3.2) sau (3.3) dupa cum obiectivul urmarit este
de maximizare sau minimizare.
Vopt = max [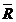 (VDi)] , i =
(VDi)] , i = 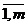 (3.2)
(3.2)
sau
Vopt = min [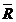 (VDi)] , i =
(VDi)] , i = 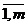 . (3.3)
. (3.3)
In desfasurarea
actiunilor economice complexe care sunt succesiuni de procese decizionale
si de procese nedecizionale, de multe ori este necesar sa se
decida nu numai in functie de rezultatele imediate asociate
variabilelor, ci si de rezultatele mai indepartate estimate ale unui
sir de procese decizionale viitoare. Acestea sunt puse in evidenta
cu ajutorul unei reprezentari grafice sub forma arborescenta - arbore
decizional.

Fig 3.2. Arbore
decizional
unde: [1], [2]
reprezinta puncte de decizie corespunzatoare unor procese
decizionale succesive;
(1.1), (1.2) -
noduri de evenimente aleatoare corespunzatoare punctului 1 de decizie
(2.1), (2.2) -
noduri de evenimente aleatoare corespunzatoare punctului 2 de decizie;
R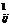 reprezinta rezultatele estimate a se obtine cu
probabilitatile p
reprezinta rezultatele estimate a se obtine cu
probabilitatile p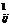 , daca se aplica variantele decizionale V
, daca se aplica variantele decizionale V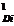 corespunzatoare punctului 1 de decizie;
corespunzatoare punctului 1 de decizie;
R reprezinta rezultatele estimate a se obtine cu
probabilitatile p
reprezinta rezultatele estimate a se obtine cu
probabilitatile p , daca se aplica variantele decizionale V
, daca se aplica variantele decizionale V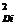 corespunzatoare punctului 2 de decizie.
corespunzatoare punctului 2 de decizie.
Pentru fundamentarea
deciziei se analizeaza graful pornind de la partea ramificata a arborelui,
conform urmatorului algoritm:
- se
calculeaza valoarea asteptata a rezultatului in nodurile de evenimente
corespunzatoare punctului [2] de decizie:
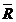 (V
(V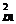 ) = R
) = R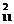 ∙ p
∙ p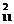 + R
+ R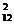 ∙ p
∙ p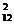 (3.4)
(3.4)
si
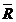 (V
(V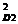 ) = R
) = R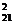 ∙ p
∙ p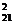 + R
+ R ∙ p
∙ p + R
+ R ∙ p
∙ p (3.5)
(3.5)
- se alege
decizia in punctul [2] prin maximizarea sau minimizarea valorilor asteptate
. Se aplica relatiile(3.6) sau (3.7);
V max [
max [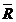 (V
(V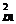 );
); 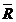 (V
(V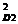 )] .(3.6)
)] .(3.6)
sau
V min [
min [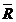 (V
(V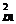 );
); 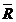 (V
(V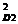 )] .(3.7)
)] .(3.7)
- se calculeaza valoarea
asteptata a rezultatului in nodurile corespunzatoare punctului
[1] de decizie;
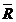 (V
(V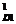 ) = R
) = R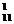 ∙ p
∙ p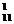 + R
+ R ∙ p
∙ p (3.8)
(3.8)
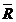 (V
(V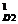 ) = R
) = R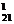 ∙ p
∙ p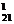 + R
+ R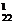 ∙ p
∙ p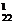 + V
+ V (3.9)
(3.9)
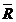 (V
(V ) = R
) = R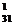 ∙ p
∙ p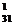 + R
+ R ∙ p
∙ p + R
+ R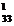 ∙ p
∙ p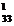 (3.10)
(3.10)
-se alege decizia in punctul [1] prin
maximizarea sau minimizarea valorilor asteptate, aplicandu-se relatia
(3.12).
V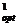 max [
max [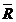 (V
(V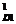 );
); 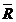 (V
(V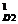 );
); 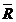 (V
(V )]
)]
sau
V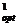 min
[
min
[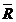 (V
(V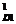 );
); 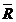 (V
(V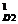 );
); 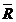 (V
(V )] (3.12)
)] (3.12)
Exemplul 1. Managerul productiei este ingrijorat in legatura cu
procentul de produse neconforme realizate de o masina recent
instalata. Pe baza studiilor efectuate, s-a stabilit ca, in prezent,
masina realizeaza cu o
probabilitate de 0,2 un procent de 1% produse neconforme, cu o probabilitate de
0,3 un procent de 5% produse neconforme, cu o probabilitate de 0,35 un procent
de 10% produse neconforme, sau 25% produse neconforme cu o probabilitate de
0.15.
Sunt analizate trei alternative
posibile de actiune. Prima este de a lasa masina asa cum
este, a doua este de a realiza o ajustare a masinii la un cost de 250 000
unitati monetare, cu garantia de a nu avea mai mult de 5%
produse neconforme, a treia consta in ajustarea masinii la un cost de
1 000 000 unitati monetare, asigurand numai 1% procent de
neconformitati.
Managerul tocmai a semnat un contract
de 1000 produse realizabile pe aceasta masina. Profitul firmei
este de 5000 unitati monetare pentru fiecare produs vandut, iar
costul remedierii produselor neconforme este de 20 000 unitati
monetare/produs.
Ce decizie ar trebui sa ia
managerul productiei in legatura cu ajustarea masinii,
pentru a obtine un profit maxim din contractul semnat?
Rezolvare
Se identifica elementele
procesului decizional: variantele decizionale, starile naturii;
rezultatele estimate a se obtine.
Varianta decizionala V1,
insemna sa lase masina asa cum este. Acestei variante ii
corespund patru stari de functionare ale masinii: procent de
defectiuni 1%, procent de defectiuni 5%, 10% sau 25%. Se calculeaza
profitul estimat a se obtine pentru cele patru stari de
functionare ale masinii:
P(1%) = 5000∙1000 -
1%∙1000∙20000 = 4 800 000 u.m
P(5%) = 5000∙1000 -
5%∙1000∙20000 = 4 000 000 u.m. .
P(10%) = 5000∙1000 -
10%∙1000∙20000 = 3 000 000 u.m
P(25%) = 5000∙1000 -
25%∙1000∙20000 = 0 u.m
Varianta decizionala V2,
insemna ajustarea masinii la un cost de 250000 u.m. Acestei variante
ii corespund doua stari de functionare ale masinii: procent
de defectiuni 1% sau procent de defectiuni 5%. Profitul estimat a se
obtine este de 4 800 000 u.m. pentru starea de 1% procent de
defectiuni si de 4 000 000 u.m. pentru 5% procent de defectiuni.
Varianta decizionala V3,
insemna ajustarea masinii la un cost de 1000000 u.m. Acestei variante
ii corespunde o singura stare de functionare a masinii, procent
de defectiuni 1% .
Se modeleaza procesul decizional
cu ajutorul unui arbore care sintetizeaza variantele decizionale,
starile naturii corespunzatoare fiecarei variante,
probabilitatile de aparitie a acestor stari si
rezultatele estimate a se obtine, exprimate prin profit (fig.3.3).
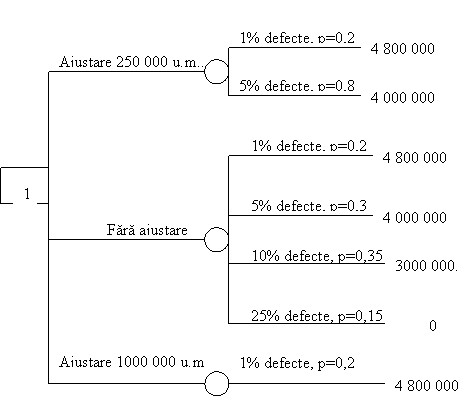
Fig. Modelarea procesului decizional
Pentru fiecare varianta
decizionala, se calculeaza profitul probabil, tinand cont
si de costurile corespunzatoare ajustarilor:
P(V2) = 4 800 000∙0,2
+ 4 000 000∙0,8 - 250 000 = 3 910 000 u.m.
P(V1) = 4 800 000∙0,2
+ 4 000 000∙0,3 + 3 000 000∙0,35 = 3210000u.m.
P(V3) = 4 800 000 - 1000000
= 3 800 000 u.m.
Se
alege varianta care corespunde profitului maxim probabil, respectiv varianta V2
(ajustarea masinii la costul de 250 000 u.m).
2. Teoria jocurilor
Teoria jocurilor este utila
pentru rezolvarea problemelor decizionale in conditii de incertitudine.
Incertitudinea este generata de existenta unor variabile (stari
ale naturii) care pot apare in cursul unei alternative de actiune si
asupra carora nu se detin informatii pentru a le putea determina
probabilitatea de aparitie. In aceste conditii, pentru fundamentarea
deciziei se pot utiliza diferite reguli de optimizare:
1.Regula pesimista enuntata de Abraham Wald propune
selectarea variantei care optimizeaza situatia cea mai
nefavorabila. In conditiile cuantificarii elementelor procesului
decizional, exprimarea matematica a acestei reguli se face prin
relatia (3.13),daca obiectivul urmarit este de maximizare a rezultatelor,
sau prin relatia (3.14), daca obiectivul este de minimizare a
rezultatelor.
Vopt.→maxi=1,m (minj=1,k
Rij) (3.13)
sau
Vopt.→mini=1,m (maxj=1,k
Rij) (3.14)
2.Regula optimista propune selectarea variantei
decizionale care optimizeaza situatia cea mai favorabila,
conform relatiei (3.15) sau(3.16).
Vopt.→maxi=1,m (maxj=1,k
Rij) (3.15)
sau
Vopt.→mini=1,m(minj=1,k
Rij) (3.16)
3.Regula optimist ponderata enuntata de Hurwicz
propune alegerea unui coeficient de optimalitate, a I (0,1) care pondereaza situatia
cea mai favorabila. Varianta decizionala optima corespunde
relatiei (3.17) sau(3.18) dupa cum obiectivul urmarit este de
maximizare sau minimizare a rezultatelor.
Vopt.→maxi=1,m[α∙maxj=1,k
Rij +(1 - α)∙minj=1,k Rij] (3.17)
sau
Vopt.→mini=1,m[α∙minj=1,k
Rij +(1 - α)∙maxj=1,k Rij] (3.18)
4.Regula proportionalitatii enuntata de Laplace
propune aplicarea metodei valorii asteptate, considerand ca
starile naturii apar cu probabilitati egale, conform
relatiei (3.19) sau(3.20).
Vopt maxi=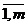 [
[ 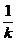
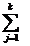 Rij (3.19)
Rij (3.19)
sau
Vopt mini=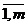 [
[ 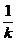
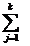 Rij (3.20)
Rij (3.20)
5.Regula minimizarii regretului enuntata de Savage
propune calculul regretului Rg cu relatia (3.21) sau(3.22) ,
dupa cum obiectivul urmarit este de maximizare sau minimizare.
||Rgij|| = ||maxi=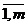 Rij - Rij|| (3.21)
Rij - Rij|| (3.21)
sau
||Rgij|| = ||Rij
- mini=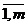 Rij|| (3.22)
Rij|| (3.22)
unde: ||Rgij||
reprezinta matricea regretelor, iar Rij reprezinta
rezultatul estimat a se obtine daca se aplica varianta
decizionala VDi in conditiile aparitiei starii Sj.
Varianta decizionala optima
este cea care minimizeaza regretul calculat conform relatiei (3.23).
Vopt mini=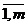 (maxj=
(maxj= Rgijj
(3.23)
Rgijj
(3.23)
Daca asupra unei probleme de
decizie se aplica toate cele cinci reguli, in cele mai multe cazuri
rezulta decizii contradictorii. In situatiile reale aplicarea uneia
din cele cinci reguli este subiectiva, depinde de optimismul sau
pesimismul decidentului. Totusi, in anumite conjuncturi, cand exista
posibilitatea de faliment sau pierderii de vieti omenesti, se impune
aplicarea minimizarii regretului, iar in situatia in care matricea
castigurilor are valori omogene, se aplica regula optimista
deoarece riscul de pierderi este minim.
Exemplul 2. Directorul tehnic are de luat o
decizie in ceea ce priveste alegerea unei variante tehnologice pentru
asimilarea in fabricatie a unui nou produs. Sunt analizate trei variante
tehnologice posibile, pentru fiecare cunoscandu-se structura cheltuielilor,
conform tabelului Pretul de vanzare
este stabilit in functie de performantele tehnice ale produsului
astfel: 126 000 u.m. pentru varianta V1; 120 000 u.m. pentru
varianta V2; 140 000 u.m. pentru variantaV3.
Toate cele trei variante tehnologice
permit realizarea a 1000 produse/an.
In urma studiilor de piata
intreprinse, s-a stabilit ca cererea pentru acest produs poate sa
varieze intre un minim de 500 produse/an si un maxim de 1000 produse/an.
Tabel Structura cheltuielilor
|
Varianta tehnologica
|
Cheltuieli variabile
|
Cheltuieli fixe
|
|
Unitati monetare/produs
|
Unitati monetare/an
|
|
V1
|
90 000
|
12 000 000
|
|
V2
|
80 000
|
15 000 000
|
|
V3
|
98 000
|
11 000 000
|
Care considerati ca este
varianta tehnologica optima, din punct de vedere economic ?
Rezolvare
Se considera trei variante
decizionale corespunzatoare celor trei variante tehnologice si
doua stari ale naturii corespunzatoare celor doua
stari ale cererii de produse,Q1 = 500 produse/an si Q2
=1000 produse/an.
Se calculeaza profitul estimat a
se obtine pentru fiecare varianta decizionala si fiecare
stare a naturii, aplicandu-se relatia generala de calcul
P = Q∙(Pv - Chv)
- ChF (3.24)
unde: P reprezinta profitul
estimat a se obtine in perioada T;
Q - cererea de produse in perioada T;
Pv - pretul unitar de
vanzare;
Chv - cheltuieli variabile
unitare;
ChF- cheltuieli fixe in perioada T
Rezulta:
P11 = 500∙(126 000 -
90 000) - 12 000 000 = 6 000 000 u.m./an
P12 = 1 000∙(126 000
- 90 000) - 12 000 000 = 24 000 000 u.m./an
P21 = 500∙(120 000 -
80 000) - 15 000 000 = 5 000 000 u.m./an
P22 = 1 000∙(120 000
- 80 000) - 15 000 000 = 25 000 000 u.m./an
P31 = 500∙(140 000 -
98 000) - 11 000 000 = 10 000 000 u.m./an
P31 = 1 000∙(140 000
- 98 000) - 11 000 000 = 23 000 000 u.m./an
Se
sintetizeaza toate informatiile de care dispunem intr-un tabel de
decizie (tab.3.4).
Tabel 3.4. Matricea profiturilor
|
Variante decizionale
|
Profit pentru starea naturii Q1=
500 produse/an
|
Profit pentru starea naturii Q2=
1000 produse/an
|
|
milioane unitati
monetare/an
|
milioane unitati
monetare/an
|
|
V1
|
6
|
24
|
|
V2
|
5
|
25
|
|
V3
|
10
|
23
|
Se aplica cele cinci reguli de
decizie din teoria jocurilor.
1. Regula pesimista:Vopt→
maxi=1,3 (minj=1,2 Pij) = max (6, 5, 10) = 10
mil.u.m. Rezulta Vopt. = V3
2. Regula optimista:Vopt→
maxi=1,3 (maxj=1,2 Pij) = max (24, 25, 23) =
25 mil. u.m. Rezulta Vopt.
= V2
3.Regula optimist ponderata.
Se alege un coeficient de optimalitate α = 0,2 astfel incat: Vopt→
maxi=1,3 [0,2∙24 + 0,8∙6; 0,2∙25+ 0,8∙5;
0,2∙23+ 0,8∙10] = maxi=1,3 [9,6; 9; 12,6] = 12,6 mil.
u.m. Rezulta Vopt =V3
4. Regula
proportionalitatii:Vopt→ max [(6+24):2;
[(5+25):2; [(10+23):2] = max (15; 15; 16,5) = 16,5 Rezulta Vopt. = V3
5.Regula minimizarii
regretului. Se calculeaza valoarea regretului cu relatia (3.21),
rezultand matricea regretelor ║Rgij║
(tabel 3.5)
Tabel 3.5. Matricea regretelor
|
Variante decizionale
|
Regretul pentru starea naturii Q1=
500 produse/an
|
Regretul pentru starea naturii Q2=
1000 produse/an
|
|
milioane unitati
monetare/an
|
milioane unitati
monetare/an
|
|
V1
|
4
|
1
|
|
V2
|
5
|
0
|
|
V3
|
0
|
2
|
Vopt→ mini=1,3
(maxj=1,2Rgij )= min (4; 5; 2) = 2 Rezulta Vopt.=V3
3. Teoria utilitatii
Teoria utilitatii
asigura fundamentarea deciziilor multicriteriale, cand evaluarea
rezultatelor corespunzatoare diferitelor variante decizionale se face prin
mai multe criterii Crl , l =  , care se exprima prin unitati de
masura diferite. De exemplu, in decizia privind achizitionarea
unui echipament de productie, se au in vedere drept criterii de decizie:
pretul de achizitie, fiabilitatea si consumul de combustibil in
exploatare. In aceste conditii se pune problema determinarii unei
unitati de masura comune, pentru a se putea analiza
comparativ diferite variante decizionale. Se normalizeaza
consecintele prin utilitati, putandu-se determina o utilitate
globala pentru fiecare varianta decizionala.
, care se exprima prin unitati de
masura diferite. De exemplu, in decizia privind achizitionarea
unui echipament de productie, se au in vedere drept criterii de decizie:
pretul de achizitie, fiabilitatea si consumul de combustibil in
exploatare. In aceste conditii se pune problema determinarii unei
unitati de masura comune, pentru a se putea analiza
comparativ diferite variante decizionale. Se normalizeaza
consecintele prin utilitati, putandu-se determina o utilitate
globala pentru fiecare varianta decizionala.
3.1 Conceptul de utilitate
In procesul decizional, utilitatea masoara
importanta pe care o are pentru decident o anumita varianta
decizionala care apartine unei multimi de variante posibile.
Cea mai completa fundamentare a
utilitatii decizionale este data de axiomatica lui Von Neuman
si O. Morgenstern. Succint, aceasta cuprinde urmatoarele
propozitii fundamentale:
a) Un decident care compara
doua variante decizionale VD1 si VD2 poate manifesta
una din urmatoarele optiuni:
VD1 VD2 varianta VD1 este
preferata variantei VD2;
VD2 varianta VD1 este
preferata variantei VD2;
VD2 VD1 varianta VD2 este
preferata variantei VD1;
VD1 varianta VD2 este
preferata variantei VD1;
VD1 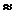 VD2 relatie de
indiferenta.
VD2 relatie de
indiferenta.
b) Fiind date trei variante
decizionale, daca un decident exprima relatia de preferinta
VD1 VD2 atunci implicit va exprima si
relatia de preferinta a unei mixturi a lui VD1 cu VD3
fata de o mixtura a lui VD2 cu VD3. In
acest fel, se pot construi cu ajutorul a doua variante VD1
si VD2 un numar infinit de mixturi care variaza
continuu pe scara preferintelor intre cele doua variante.
VD2 atunci implicit va exprima si
relatia de preferinta a unei mixturi a lui VD1 cu VD3
fata de o mixtura a lui VD2 cu VD3. In
acest fel, se pot construi cu ajutorul a doua variante VD1
si VD2 un numar infinit de mixturi care variaza
continuu pe scara preferintelor intre cele doua variante.
Plecand de la aceasta
axiomatica se poate determina functia de utilitate
corespunzatoare unui proces decizional.
3.2 Functia de utilitate
Functia de utilitate
caracterizeaza preferintele decidentului pentru un anumit rezultat Rilk
din cadrul unui criteriu. Pentru a exprima functia de utilitate U(R),
se alege arbitrar o scala adimensionala [0,1] astfel incat:
- Umin = 0, se acorda
utilitatea minima celui mai nefavorabil rezultat din cadrul unui criteriu;
- Umax = 1, se acorda
utilitatea maxima celui mai favorabil rezultat din cadrul unui criteriu.
Daca criteriile de decizie se
ierarhizeaza cu un coeficient de importanta Kj I[0,5;1],
utilitatile se vor acorda astfel:
- Umin = 1-Kj ;
- Umax = Kj
Pentru un rezultat intermediar cuprins
intre cele doua valori extreme, utilitatea se determina prin
interpolare. Daca utilitatile variaza direct
proportional cu rezultatele, se aplica (3.25), iar pentru o
variatie invers proportionala, se aplica (3.26).
U(Ri) = Umin.+
(Umax - Umin.) ∙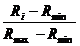 (3.25)
(3.25)
sau
U(Ri) = Umin.+
(Umax - Umin.)∙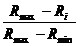 (3.26)
(3.26)
unde: Rmin / Rmax
reprezinta valorile minime respectiv maxime ale rezultatelor estimate a se
obtine in cadrul unui criteriu de decizie ;
U(Ri) - utilitatea
calculata pentru un rezultat intermediar.
3.3 Fundamentarea deciziei
Fiecarui rezultat din matricea
prezentata in tabelul (3.1) i se va asocia o utilitate conform regulilor
prezentate in § 3.2. Se obtine matricea utilitatilor (tabelul 3.6).
Tabel 3.6.Matricea utilitatilor
|
Starile naturii
Criterii
decizie
Variante
decizionale
|
S1
|
Sj
|
Sk
|
|
Cr1
|
Crl..
|
Crn
|
Cr1
|
Crl..
|
Crn
|
Cr1
|
Crl
|
Crn
|
|
VD1
|
U111
|
U 1l1
|
U 1n1
|
U 11j
|
U 1lj
|
U 1nj
|
U 11k
|
U 1lk
|
U 1nk
|
|
VDi
|
U i11
|
U il1
|
U in1
|
U i1j
|
U ilj
|
U inj
|
U i1k
|
U ilk
|
U ink
|
|
VDm
|
U m11
|
U ml1
|
U mn1
|
U m1j
|
U mlj
|
U mnj
|
U m1k
|
U mlk
|
U mnk
|
Pentru fundamentarea deciziei se
calculeaza o valoare globala a utilitatii Ug(VDi)
corespunzatoare fiecarei variante decizionale. Calculul
utilitatii globale se face diferit in functie de incadrarea
procesului decizional. Astfel, in conditii de certitudine se aplica
relatia (3.27) iar pentru conditii de risc se aplica (3.28).
Ug(VDi) = 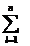 Uil1 (3.27)
Uil1 (3.27)
Ug(VDi) = p1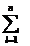 Uil1 + pj
Uil1 + pj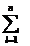 Uilj + pk
Uilj + pk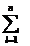 Uilk.(3.28)
Uilk.(3.28)
Varianta decizionala optima este
aceea care prezinta maximum de utilitate globala (3.29).
Vopt maxi=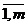 [Ug(VDi)] .(3.29)
[Ug(VDi)] .(3.29)
Exemplul 3. O societate comerciala a primit o oferta de cooperare
pentru fabricarea unui anumit tip de masina, din partea a trei
parteneri straini. Performantele tehnice ale celor trei tipuri de
masini sunt diferentiate, ceea ce genereaza consecinte
economice diferite. Se iau in considerare urmatoarele criterii de decizie:
- productia fizica
anuala , cu un coeficient de importanta K1 = 0,8;
- consumul de energie electrica ,
cu un coeficient de importanta K2= 0,6;
- profitul anual obtinut, cu
coeficientul de importanta K3 = 0,9;
- ponderea productiei de
calitatea I, cu coeficientul de importanta K4=1.
Matricea consecintelor economice
asociate fiecarui tip de masina si criteriu de decizie se
prezinta in tabelul 2.7.
Tabel 2.7.Matricea consecintelor
economice
|
Variante decizionale
|
Productia fizica
|
Consum de energie electrica
|
Profit
|
Ponderea productiei de
calitatea I
|
|
Kg/an
|
Kw/ora
|
Mii lei/an
|
|
|
M1
|
62 000
|
4,5
|
2480
|
92
|
|
M2
|
65 000
|
4,1
|
2568
|
88
|
|
M3
|
78 000
|
4,8
|
3003
|
84
|
|
Coeficient de importanta
|
0,8
|
0,6
|
0,9
|
1
|
Efortul investitional solicitat
de asimilarea in fabricatie a noului tip de masina este acelasi
in cele trei variante. Sa se aleaga varianta optima .
Rezolvare
Se inlocuiesc consecintele
economice cu utilitati, analizandu-se valorile corespunzatoare
fiecarui criteriu de decizie.
Astfel, pentru criteriul productia
fizica,consecinta cea mai favorabila este valoarea de 78
000kg/an careia i se va acorda utilitatea 0,8, iar consecinta cea mai
nefavorabila este valoarea de 62 000kg/an careia i se va acorda
utilitatea de 0,2. Pentru valoarea intermediara de 65 000 kg/an utilitatea se calculeaza cu relatia
(3.25).
Pentru criteriul consum de energie
electrica, consecinta cea mai favorabila este 4,1
kw/ora careia i se va acorda utilitatea 0,6, iar consecinta cea
mai nefavorabila este 4,8 kw/ora careia i se va acorda
utilitatea 0,4. Pentru valoarea de 4,5 kw/ora utilitatea se va calcula cu
relatia (3.26).
Pentru criteriul profit,consecinta
cea mai favorabila este valoarea de 3003 mii lei/an careia i se va
acorda utilitatea 0,9, iar consecinta cea mai nefavorabila este
valoarea de 2480 mii lei/an careia i se va acorda utilitatea de 0,1.
Pentru valoarea intermediara de 2568 mii lei/an utilitatea se calculeaza cu relatia
(3.25). Similar se calculeaza
utilitatile pentru criteriul ponderea productiei de calitatea
I.
Rezulta matricea
utilitatilor din tabelul 3.8.
Tabel 3.8.Matricea utilitatilor
|
Variante decizionale
|
Utilitatea pentru productia
fizica
|
Utilitatea pentru consum energie electrica
|
Utilitatea pentru profit
|
Utilitatea pentru ponderea productiei de calitatea I
|
|
M1
|
0,2
|
0,48
|
0,1
|
1
|
|
M2
|
0,21
|
0,6
|
0,25
|
0,5
|
|
M3
|
0,8
|
0,4
|
0,9
|
0
|
Pentru fiecare varianta se calculeaza
o utilitate globala, cu (3.28).
Se
obtin urmatoarele valori ale utilitatilor:
U(M1) = 0,2 + 0,48 + 0,1 +1
= 1,78
U(M2) = 0,21 + 0,6 + 0,25
+0,5 = 1,56
U(M3) = 0,8 + 0,4 + 0,9 +0
= 2,1
Se observa ca:U(M3)
> U(M1) > U(M2) Rezulta, varianta M3
este preferata celorlalte doua variante.
4. Metode ale cercetarii
operationale
Cercetarile operationale
initiate de Kauffman reprezinta modele matematice cu algoritmi
specifici de rezolvare.
Modelele matematice sunt modele
abstracte care descriu in termeni cantitativi structura reala a unui
sistem. Astfel de modele se aplica pentru optimizarea unor
activitati, cand in functionarea acestora sunt identificate
variabile care se pot cuantifica si intre care se pot stabili relatii
de interdependenta care sunt exprimate prin ecuatii sau
inecuatii.
Utilizarea modelelor matematice in
fundamentarea deciziilor presupune parcurgerea logica a urmatoarelor
etape:
- definirea problemei de rezolvat prin
colectarea de date privind modul de desfasurare in timp a
activitatii care se optimizeaza;
- construirea modelului matematic prin
identificarea variabilelor si a ecuatiilor care descriu
interdependenta dintre acestea;
- alegerea unui criteriu de
eficienta pentru activitatea respectiva (venituri, costuri,
timp, numar piese) si optimizarea criteriului ales, respectiv
maximizare sau minimizare;
- rezolvarea modelului prin algoritmi
specifici si analiza de sensibilitate prin acordarea de valori diferite
variabilelor;
- validarea modelului si
aplicarea in practica.
Cele mai uzuale metode ale
cercetarii operationale utilizate in fundamentarea deciziilor sunt:
- programarea liniara si
neliniara prin care se asigura:optimizarea planului de
productie, optimizarea planului de transport, alocarea optima a
resurselor, stabilirea celui mai ieftin program de inlocuire a echipamentelor
uzate;
- teoria firelor de asteptare
prin care se asigura minimizarea timpului de asteptare in depozite
sau magazii;
- teoria stocurilor pentru
dimensionarea optima a stocurilor de productie, in conditiile
asigurarii ritmicitatii productiei si a unor costuri
minime de lansare, depozitare.
3.4.Proces
decizional de grup
In mod
obisnuit, deciziile in cadrul intreprinderii sunt luate de echipe
multidisciplinare (grupuri constituite din angajati sau specialisti
din diverse domenii de activitate). De exemplu, grupurile sunt adesea
solicitate sa decida ce produse noi trebuie oferite clientilor,
cum trebuie imbunatatite politicile de promovare, cum se poate
imbunatati calitatea, etc.
Participarea
grupului la luarea deciziilor este cunoscuta in teoria manageriala
sub denumirea de management participativ.
Managementul
participativ este definit ca reprezentand o metoda de management
bazata pe atragerea salariatilor sub forma consultativa sau
deliberativa , in procesul de luare a deciziilor, in scopul cresterii
eficientei, folosind in acest scop mecanisme economice, organizatorice,
juridice si psiho-sociologice.
Managementul
participativ are doua forme de aplicare:
a)de natura
consultativa - se bazeaza pe consultarea grupului asupra
modalitatilor de solutionare a diferitelor probleme decizionale.
Se recomanda practicarea acestei forme de management participativ in toate
compartimentele si la toate nivelurile ierarhice, autoritatea de a lua
deciziile se atribuie sefului de compartiment.
b)de natura
deliberativa - se caracterizeaza prin adoptarea in grup a deciziilor
respectandu-se anumite cerinte organizatorice, economice, juridice.
Aceasta forma se aplica prin institutionalizarea unor
organe ale managementului participativ (de exemplu, consiliul de
administratie).
Principalele
avantaje ale utilizarii grupului in luarea deciziilor sunt:
−sunt
folosite mai multe cunostinte si informatii, ca urmare, se
pot identifica mai multe variante decizionale, deci creste probabilitatea
alegerii variantei optime;
−oamenii se
vor implica mult mai mult in implementarea unei decizii, daca au
contribuit la fundamentarea ei.
Exista, de
asemenea, si cateva dezavantaje ale folosirii grupurilor cum ar fi:
−prelungirea
timpului si costului luarii deciziei, deoarece este nevoie de mai
mult timp pentru ascultarea si analizarea punctului de vedere al
fiecarui membru al grupului;
−o
singura persoana poate domina si influenta grupul;
−deciziile
grupului pot fi de o calitate mai redusa daca, din dorinta de a
nu intra in conflict, unii membrii refuza sa-si exprime deschi
punctul de vedere.
Cu toate acestea,
luarea deciziilor in grup privind rezolvarea unor probleme complexe din
organizatie, reprezinta una din provocarile managementului
modern.
Principalele
metode care pot fi utilizate pentru cresterea eficientei deciziilor
de grup sunt: tehnica Brainstorming, tehnica Delphi, tehnica nominala a
grupului.
1.Tehnica
Brainstorming (furtuna creierelor)reprezinta un proces de luare a
deciziilor in grup, utilizat pentru identificarea unui numar cat mai mare
de alternative posibile privind solutionarea unei probleme decizionale
(gasirea cat mai multor variante decizionale). Acest proces se desfasoara
sub forma unei sedinte, in care fiecare participant propune o
solutie pentru rezolvarea problemei pusa in discutie (fig.3.4).
Se interzic reactiile negative din partea oricarui membru al grupului
fata de alternativele sugerate, pana ce toti membrii vor
prezenta alternativele pe care le percep drept valoroase.

Fig. 3.4. Procesul de
brainstorming
Aceasta
metoda ofera avantajul exprimarii cat mai multor idei utile, dar
si dezavantajul irosirii timpului grupului cu idei care nu pot fi
transpuse in practica.
2.Tehnica
nominala a grupului este un proces, in care fiecarui membru al
grupului ii este asigurata o participare egala la luarea deciziilor.
Se parcurg urmatoarele etape:
−fiecare
membru al grupului isi scrie propriile idei privind rezolvarea problemei
analizate;
−fiecare
membru isi prezinta ideile in fata grupului;
−grupul
discuta simultan ideile prezentate, discutiile avand caracter spontan
si neorganizat;
−cand se
incheie discutia, se organizeaza un vot secret pentru a permite
membrilor sa sprijine fara nici o teama ideile pe care le
agreeaza. Ideea care primeste cele mai multe voturi este
adoptata si implementata.
Principalul
dezavantaj al acestei metode, este ca nu se poate stii motivul pentru
care oamenii au votat o anumita idee.
3.Tehnica Delphi se bazeaza
pe utilizarea unui grup de specialisti fara ca acestia
sa discute fata in fata. Etapele formale ale acestei
tehnici sunt urmatoarele:
−identificarea
problemei de rezolvat si conceperea unui chestionar;
−membrii
grupului sunt solicitati sa vina cu solutii la aceasta
problema, prin completarea anonima a chestionarului;
−raspunsurile
sunt centralizate si trimise tuturor membrilor grupului;
−membrii
grupului sunt solicitati sa ofere o noua solutie la
problema, dupa ce au studiat raspunsurile centralizate;
−etapele 3
si 4 se repeta , pana ce se ajunge la un consens privind
solutia problemei.
Avantajul acestei
metode este acela ca se pot consulta specialisti din intreaga lume,
dar cu dezavantajul ca acestia nu pot comunica intre ei.
Concluzii
Decizia este
rezultatul unui proces, prin care se alege dintr-o multime de variante
posibile de actiune, varianta considerata optima, in ceea ce
priveste realizarea unui obiectiv.
In functie
de obiectivul urmarit, deciziile pot fi :strategice, tactice, operationale.
In functie
de caracterul informatiilor de care dispune decidentul, deciziile sunt
luate in conditii de : certitudine, risc, incertitudine.
In functie
de numarul criteriilor de decizie distingem: decizii unicriteriale,
decizii multicriteriale.
Procesul
decizional se bazeaza pe conceptul de sistem, avand urmatoarea
structura: elemente de intrare − informatii ; elemente de
iesire − decizia; elemente componente − formularea problemei,
identificarea solutiilor de rezolvare, identificarea conditiilor de
desfasurare a actiunii, estimarea consecintelor economice,
fundamentarea solutiei optime; feed-back − transmiterea, aplicarea
si masurarea rezultatelor implementarii deciziei.
Pentru
fundamentarea deciziei se utilizeaza o serie de metode cum ar fi: teoria
probabilitatii, teoria jocurilor, teoria utilitatii, metode
ale cercetarii operationale.
Procesele
decizionale de grup au atat avantaje cat si dezavantaje. Se bazeaza
pe folosirea unor tehnici specifice.
Test de
autoevaluare
Studiu de caz. Managerul unei
intreprinderi de produse lactate are de luat o decizie privind dezvoltarea in
perspectiva a firmei. In acest scop, solicita departamentului de
cercetare dezvoltare sa elaboreze cat mai multe variante posibile de
dezvoltare a productiei. In urma studiilor intreprinse,a analizei si
sintezei informatiilor interne si externe, au rezultat
urmatoarele patru variante:
Varianta 1 presupune achizitionarea unei
linii tehnologice, pe langa cele existente, ceea ce va asigura o
crestere a productiei la 3000 tone/zi, fata de numai 2000
tone/zi cat produce in prezent intreprinderea. Aceasta crestere a
productiei necesita angajarea a inca trei soferi si 15
muncitori. Durata de realizare a acestui proiect se estimeaza la trei luni
si necesita un volum de investitii de 120 milioane lei. De
asemenea, se estimeaza ca, dupa punerea in aplicare a
proiectului se va obtine un profit zilnic de 90 000 lei.
Varianta 2 presupune achizitionarea a patru linii tehnologice din
strainatate si dublarea suprafetei actualelor cladiri.
Fiecare linie tehnologica achizitionata necesita pentru
buna functionare, 12 muncitori si are o capacitate de 2000 tone/zi.
Dezvoltarea activitatii necesita angajarea a 4 soferi
pentru colectarea laptelui cu cisternele, 20 muncitori indirect productivi, 3 persoane
la serviciul desfacere, o secretara si un contabil sef. Punerea
in functiune a liniilor tehnologice precum si
imbunatatirile aduse capacitatii de care dispune
intreprinderea, se pot realiza in 8 luni, vor necesita un fond de
investitii de 480 milioane lei si vor asigura un profit de 300 000
lei/zi.
Varianta 3 consta in cumpararea unei
intreprinderi de produse lactate care actualmente are dificultati.
Aceasta intreprindere dispune de o linie tehnologica cu o
productie zilnica de 1000 tone si foloseste 30
salariati. Achizitionarea intreprinderii si reorganizarea
intregii activitati precum si achizitionarea a inca
doua linii tehnologice din strainatate va necesita un volum de
investitii de 360 milioane lei. Aplicarea acestei variante de dezvoltare
se estimeaza la 2 luni si va asigura un profit de 120 000 lei/zi.
Varianta 4 consta in amenajarea unei
suprafete de productie pentru instalarea a inca doua linii
tehnologice ce se vor achizitiona de pe piata interna. Fiecare
linie nou instalata va necesita angajarea a inca 18 muncitori si
va produce cate 3000 tone/zi. Dezvoltarea va presupune un numar
suplimentar de angajati si anume, 6 muncitori indirect productivi, 3
soferi si o persoana la serviciul desfacere. Aceasta
varianta se estimeaza ca se poate implementa in 5 luni, cu un
volum de investitii de 125 milioane lei. Dupa punerea in aplicare a
proiectului se estimeaza obtinerea unui profit zilnic de 270 000 lei.
Tema
1.Identificati tipul deciziei.
2.Identificati elementele
componente ale procesului decizional.
3.Care din metodele de fundamentare a
deciziei, considerati ca se poate aplica in aceasta
situatie?
4.Care varianta de dezvoltare o
considerati optima, daca se iau in considerare cinci criterii de
decizie, in conditii de echivalenta ?
5.Alegeti varianta optima de dezvoltare, prin
acordarea unui coeficient de importanta diferit pentru fiecare
criteriu decizional
 |

|
Management
|
|
|
Referate pe aceeasi tema
|
|
| Ramai informat |
Informatia de care ai nevoie
Acces nelimitat la mii de documente. Online e mai simplu. |
Contribuie si tu!
Adauga online documentul tau.
|
|
|
| |












