
| Afaceri | Agricultura | Comunicare | Constructii | Contabilitate | Contracte |
| Economie | Finante | Management | Marketing | Transporturi |
Economie
|
|
Qdidactic » bani & cariera » economie Studiul modelului liniar cind ipotezele clasice asupra erorilor nu mai sunt realizate |
Studiul modelului liniar cind ipotezele clasice asupra erorilor nu mai sunt realizate
STUDIUL MODELULUI LINIAR CIND IPOTEZELE CLASICE ASUPRA ERORILOR NU MAI SUNT REALIZATE
1. Ipoteza de independenta a erorilor
S-a studiat anterior modelul liniar de regresie sub ipoteza ca
erorile sunt independente. In cazul in care erorile et sunt corelate, matricea de varianta si
covarianta a erorilor We nu se mai reduce la ![]() , iar estimatorii parametrilor modelului general Y=Xa+e, cu E(et)=0,
t=1,2,,T si
, iar estimatorii parametrilor modelului general Y=Xa+e, cu E(et)=0,
t=1,2,,T si ![]() nu mai poseda
aceleasi proprietati ca in cazul erorilor independente.
nu mai poseda
aceleasi proprietati ca in cazul erorilor independente.
Fie ![]() vectorul estimatorilor
parametrilor a. Estimatorul
vectorul estimatorilor
parametrilor a. Estimatorul ![]() trebuie sa fie
liniar in raport cu variabilele endogene Y,
adica
trebuie sa fie
liniar in raport cu variabilele endogene Y,
adica ![]() , unde M este o
matrice de coeficienti. Estimatorul
, unde M este o
matrice de coeficienti. Estimatorul ![]() este nedeplasat
deoarece:
este nedeplasat
deoarece:
![]()
(pentru ca
![]() ).
).
Pentru ca ![]() trebuie sa
impunem conditia MX=I, rezultand
ca:
trebuie sa
impunem conditia MX=I, rezultand
ca:
![]()
Matricea de varianta
si covarianta a estimatorilor (tinind cont ca ![]() ) este:
) este:
![]()
Punind
conditia ca ![]() sa fie
minimala, sub restrictia MX=I
si rezolvind aceasta problema de extremum conditionat,
rezulta ca matricea M este
de forma:
sa fie
minimala, sub restrictia MX=I
si rezolvind aceasta problema de extremum conditionat,
rezulta ca matricea M este
de forma: ![]()
Prin inlocuire si calcul se obtine:
![]()
![]()
Estimatorul ![]() astfel obtinut
este un estimator liniar, nedeplasat si de dispersie minima. El a
fost obtinut prin MCMMP generalizata. Se observa imediat ca
daca erorile sunt independente, adica
astfel obtinut
este un estimator liniar, nedeplasat si de dispersie minima. El a
fost obtinut prin MCMMP generalizata. Se observa imediat ca
daca erorile sunt independente, adica ![]() , atunci
, atunci ![]() , adica regasim estimatorul obtinut prin MCMMP
obisnuita.
, adica regasim estimatorul obtinut prin MCMMP
obisnuita.
In cazul in care erorile sunt corelate, determinarea estimatorului ![]() necesita
cunoasterea matricei de varianta si covarianta a
erorilor
necesita
cunoasterea matricei de varianta si covarianta a
erorilor ![]() . In aplicatii, deoarece
. In aplicatii, deoarece ![]() este necunoscuta,
se lucreaza cu estimatia ei
este necunoscuta,
se lucreaza cu estimatia ei ![]() , ceea ce nu antreneaza erori prea grave.
, ceea ce nu antreneaza erori prea grave.
Corelarea erorilor ![]() poate imbraca
diverse forme. Cel mai frecvent se studiaza cazul cand
poate imbraca
diverse forme. Cel mai frecvent se studiaza cazul cand ![]() (se spune ca
erorile urmeaza un proces autoregresiv de ordinul intai).
(se spune ca
erorile urmeaza un proces autoregresiv de ordinul intai).
Modelul liniar general Y=Xa+e, scris si sub forma:
(1) ![]() , t=1, 2, ,T
, t=1, 2, ,T
(in care ![]() , iar asupra erorilor
, iar asupra erorilor ![]() facem ipotezele
cunoscute:
facem ipotezele
cunoscute: ![]() ,
, ![]() , pentru
, pentru ![]() si
si ![]() ), poate fi pus sub urmatoarea forma:
), poate fi pus sub urmatoarea forma:
- ecuatia (1) scrisa pentru t-1 este: ![]() pe care o
inmultim cu r (presupunem
pe care o
inmultim cu r (presupunem ![]() ):
):
(2) ![]()
Prin scaderea (1)-(2) obtinem:
(3) ![]()
Daca s-ar cunoaste parametrul r, atunci ecuatia (3) ar putea fi scrisa sub forma:
(4) ![]()
unde: ![]()
![]() , i=1,2,,p.
, i=1,2,,p.
![]()
Deoarece, prin ipoteze, erorile ![]() sunt independente, se
poate aplica MCMMP obisnuita ecuatiei (4) care va conduce la
estimatorul
sunt independente, se
poate aplica MCMMP obisnuita ecuatiei (4) care va conduce la
estimatorul ![]() nedeplasat si de
minima dispersie.
nedeplasat si de
minima dispersie.
Dar, cum parametrul r nu este cunoscut, pentru estimarea parametrilor unei ecuatii de
regresie atunci cand erorile sunt corelate (sub forma unui proces autoregresiv
de ordinul I, ![]() , stationar, adica media
, stationar, adica media ![]() si dispersia
si dispersia ![]() sunt independente de
timp, iar
sunt independente de
timp, iar ![]() ) se pot aplica urmatoarele metode:
) se pot aplica urmatoarele metode:
Metoda I:
1.
Se aplica MCMMP
obisnuita ecuatiilor (1) fara a tine cont ca
erorile ![]() sunt corelate. Se
obtine estimatorul
sunt corelate. Se
obtine estimatorul ![]() al lui a si se determina valorile
ajustate
al lui a si se determina valorile
ajustate ![]() si
estimatiile erorilor
si
estimatiile erorilor ![]() .
.
2.
Dam o estimare a parametrului
r aplicand MCMMP
obisnuita ecuatiei ![]() , obtinand
, obtinand ![]() .
.
3.
Inlocuim r cu ![]() in ecuatia (3)
si aplicam MCMMP obisnuita acestei ecuatii. Se
obtine estimatorul
in ecuatia (3)
si aplicam MCMMP obisnuita acestei ecuatii. Se
obtine estimatorul ![]() pentru parametrul a.
pentru parametrul a.
Evident, pentru esantioane mici, estimatorul ![]() nu prezinta
garantii ca are proprietatile dorite.
nu prezinta
garantii ca are proprietatile dorite.
Metoda II:
Ecuatia (3) de mai inainte se poate scrie si sub forma:
(5) ![]()
Se aplica MCMMP obisnuita ecuatiilor (3) si (5) astfel:
1.
Dam o valoare initiala lui r, de exemplu r0=0 in ecuatia (3)
si obtinem o prima estimatie a parametrilor ![]()
2.
Inlocuim ![]() in ecuatia (5) si efectuand
regresia, obtinem o noua valoare pentru r, notata r1
in ecuatia (5) si efectuand
regresia, obtinem o noua valoare pentru r, notata r1
3.
Inlocuim r cu r1 in
ecuatia (3) si efectuam o noua regresie, obtinand
estimatorul ![]() s.a.m.d.
s.a.m.d.
4.
Se opresc iteratiile daca valorile gasite in doua iteratii
succesive nu difera decat printr-un numar oricat de mic dorit (se
spune ca estimatorii ![]() , i=1,2, converg).
, i=1,2, converg).
Metoda III (baleiaj):
Presupunem ca ![]() , ia succesiv valorile:
, ia succesiv valorile:
![]() .
.
Aplicam MCMMP obisnuita ecuatiei (3) pentru
fiecare valoare a lui r si calculam reziduurile ![]() . Se retine valoarea lui r care da cea mai mica suma a patratelor erorilor
. Se retine valoarea lui r care da cea mai mica suma a patratelor erorilor ![]() , careia ii corespund estimatorii
, careia ii corespund estimatorii ![]() ai parametrilor.
ai parametrilor.
Exista si alte proceduri de estimare a parametrilor in cazul cand erorile sunt corelate.
1.1. Testarea ipotezei de independenta a erorilor
Atunci cand ipotezele fundamentale ale modelului liniar al regresiei
nu sunt indeplinite proprietatile estimatorilor parametrilor
sufera. Astfel, sub ipoteza I2 referitoare la distributia
erorilor si la independenta lor, estimatorii obtinuti sunt
nedeplasati si au varianta minimala. Daca erorile sunt
corelate, estimatorii raman, in general, nedeplasati, dar matricea de
varianta si covarianta a acestora nu mai este ![]() . Pentru a ne asigura de independenta erorilor trebuie
sa efectuam teste. Este vorba despre testul lui Durbin si
Watson.
. Pentru a ne asigura de independenta erorilor trebuie
sa efectuam teste. Este vorba despre testul lui Durbin si
Watson.
Modelul liniar general al regresiei:
![]()
se poate scrie sub forma:
![]()
unde: ![]() si
si 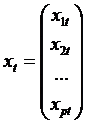 .
.
Se aplica MCMMP obisnuita si se obtine un
estimator ![]() , calculandu-se valorile ajustate
, calculandu-se valorile ajustate ![]() si erorile
estimate
si erorile
estimate ![]() .
.
Reziduurile estimate depind de sirul erorilor ![]() si de sirul
valorilor exogene
si de sirul
valorilor exogene ![]() , deoarece:
, deoarece:
![]() .
.
Se considera variabila aleatoare, notata ![]() , numita si statistica Durbin-Watson definita
prin ecuatia:
, numita si statistica Durbin-Watson definita
prin ecuatia:
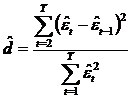 .
.
Durbin si Watson au determinat densitatea de probabilitate a
variabilei aleatoare ![]() , notata
, notata ![]() si au aratat
ca oricare ar fi sirul de exogene considerate, curbele reprezentative
ale lui
si au aratat
ca oricare ar fi sirul de exogene considerate, curbele reprezentative
ale lui ![]() oscileaza intre
doua curbe limita
oscileaza intre
doua curbe limita ![]() si
si ![]() . Aceste functii depind de numarul de
observatii (T), de numarul
de variabile exogene veritabile ce figureaza in model (m) si de sirul erorilor
. Aceste functii depind de numarul de
observatii (T), de numarul
de variabile exogene veritabile ce figureaza in model (m) si de sirul erorilor ![]() . Cele doua curbe limita (reprezentate grafic in
figura) sunt atinse pentru anumite siruri de exogene xt si sunt simetrice in
raport cu axa de abscisa 2.
. Cele doua curbe limita (reprezentate grafic in
figura) sunt atinse pentru anumite siruri de exogene xt si sunt simetrice in
raport cu axa de abscisa 2.
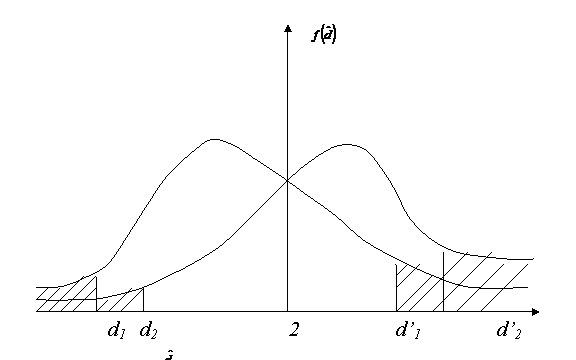

Scopul este de a sti daca erorile modelului sunt
autocorelate. Cel mai frecvent se cauta testarea legaturii erorilor
printr-o relatie de forma ![]() . Se spune ca erorile urmeaza un proces
autoregresiv de ordinul intai.
. Se spune ca erorile urmeaza un proces
autoregresiv de ordinul intai.
Vrem sa testam ipoteza I0: ![]() (absenta
autocorelatiei erorilor), contra ipotezei I1:
(absenta
autocorelatiei erorilor), contra ipotezei I1: ![]() (erorile
(erorile ![]() sunt autocorelate).
sunt autocorelate).
La un nivel de semnificatie a dat, Durbin si Watson au determinat doua valori, d1 si d2, in functie de numarul de observatii (T) si de numarul de exogene veritabile (m) corespunzatoare fiecareia din curbele limita.
Se calculeaza statistica ![]() cu relatia
data si se observa ca:
cu relatia
data si se observa ca:
1. daca ![]() , atunci se accepta I1;
, atunci se accepta I1;
2.
daca ![]() , atunci
exista indoieli ca legatura dintre erori este de forma
, atunci
exista indoieli ca legatura dintre erori este de forma ![]()
3. daca ![]() , atunci se accepta I0.
, atunci se accepta I0.
In tabelul urmator sunt date cateva valori uzuale pentru d1 si d2 in functie de T si m, pentru nivelul de semnificatie a=0,05:
Tabela D-W
|
T |
m=1 |
m=2 |
m=3 |
m=4 |
m=5 |
|||||||||
|
d1 |
d2 |
d1 |
d2 |
d1 |
d2 |
d1 |
d2 |
d1 |
d2 |
|||||
|
15 |
1,08 |
1,36 |
0,96 |
1,54 |
0,82 |
1,75 |
0,69 |
1,97 |
0,56 |
2,21 |
||||
|
20 |
1,20 |
1,41 |
1,10 |
1,54 |
1,00 |
1,68
|
0,90 |
1,83 |
0,79 |
1,99 |
||||
|
30 |
1,35 |
1,49 |
1,28 |
1,57 |
1,21 |
1,65 |
1,14 |
1,74 |
1,07 |
1,83 |
||||
|
50 |
1,50 |
1,59 |
1,46 |
1,63 |
1,42 |
1,67 |
1,38 |
1,72 |
1,34 |
1,77 |
||||
|
100 |
1,65 |
1,69 |
1,63 |
1,72 |
1,61 |
1,74 |
1,59 |
1,76 |
1,57 |
1,78 |
||||
Observatii
1. In
loc sa testam ![]() contra
contra ![]() , se poate testa I0:
, se poate testa I0: ![]() , contra I1:
, contra I1: ![]() . Se obtin doua valori
. Se obtin doua valori ![]() si
si ![]() simetrice in
raport cu 2 si se constata ca:
simetrice in
raport cu 2 si se constata ca:
a.
daca ![]() sau
sau ![]() , atunci se accepta I1;
, atunci se accepta I1;
b.
daca ![]() sau
sau ![]() , atunci exista indoieli ca erorile sunt corelate;
, atunci exista indoieli ca erorile sunt corelate;
c.
daca ![]() , atunci se accepta I0.
, atunci se accepta I0.
2.
Daca modelul studiat nu contine constanta, trebuie sa
determinam ![]() ca si cand
modelul ar contine o constanta.
ca si cand
modelul ar contine o constanta.
3. Statistica Durbin-Watson aplicata pe un model care contine variabile endogene retardate este deplasata catre 2, ceea ce inseamna ca erorile sunt mai putin corelate intr-un proces autoregresiv, decat intr-un proces ordinar.
1.2. Experienta de calcul
I. Se cunosc urmatoarele date referitoare la evolutia in timp a unei variabile economice (in preturi constante):
|
t |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
yt |
662,3 |
669,4 |
912,7 |
935,2 |
1027,2 |
1145,0 |
1193,7 |
1224,1 |
|
t |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
yt |
1281,7 |
1426,3 |
1376,2 |
1327,8 |
1420,6 |
1933,9 |
2023,4 |
|
Pe aceasta serie cronologica, utilizind
modelul ![]() ,s-a aplicat MCMMP, obtinandu-se
estimatorii:
,s-a aplicat MCMMP, obtinandu-se
estimatorii:
![]() ;
; ![]()
De asemenea, s-a calculat varianta
estimatorilor si ecartul-tip al acestora: ![]()
![]() si valorile ajustate ale variabilei endogene
si valorile ajustate ale variabilei endogene ![]() si ale reziduurilor
si ale reziduurilor ![]()
|
t |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
664,2 |
746,1 |
828,0 |
909,8 |
991,7 |
1073,6 |
1155,5 |
1237,3 |
|
t |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
|
1319,2 |
1401,0 |
1482,9 |
1564,6 |
1646,6 |
1728,5 |
1810,4 |
|
|
t |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
-1,93 |
-76,79 |
+84,79 |
+25,35 |
+35,49 |
+71,44 |
+38,30 |
-13,25 |
|
t |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
|
-37,54 |
+25,25 |
-106,64 |
-237,01 |
-226,00 |
+205,42 |
+213,03 |
|
Ne propunem sa cercetam o eventuala autocorelare a erorilor.
Rezolvare:
Pentru a putea utiliza testul Durbin-Watson trebuie ca numarul de observatii T sa fie suficient de mare (in practica T>15), iar modelul sa contina un termen constant.
Statistica Durbin-Watson definita de ecuatia 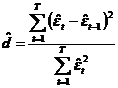 conduce, conform
datelor din tabel, la:
conduce, conform
datelor din tabel, la: ![]() .
.
Durbin si Watson au aratat ca pentru un proces
stationar (primele doua momente ale variabilei aleatoare ![]() independente de timp),
valoarea calculata a statisticii
independente de timp),
valoarea calculata a statisticii ![]() este cuprinsa
intre 0 si 4, cu absenta corelatiei in vecinatatea lui 2.
Intre aceste valori limita, tabela D-W furnizeaza, la pragul de
seminificatie a, diferite intervale de valori
este cuprinsa
intre 0 si 4, cu absenta corelatiei in vecinatatea lui 2.
Intre aceste valori limita, tabela D-W furnizeaza, la pragul de
seminificatie a, diferite intervale de valori ![]() corespunzatoare
prezentei autocorelatiei pozitive sau negative, absentei
autocorelatiei si situatiilor de indecizie, astfel:
corespunzatoare
prezentei autocorelatiei pozitive sau negative, absentei
autocorelatiei si situatiilor de indecizie, astfel:
1.
daca ![]() , atunci
erorile sunt pozitiv autocorelate;
, atunci
erorile sunt pozitiv autocorelate;
2. daca ![]() , atunci exista indoieli ca erorile ar fi corelate;
, atunci exista indoieli ca erorile ar fi corelate;
3. daca ![]() , atunci erorile
, atunci erorile ![]() sunt independente;
sunt independente;
4. daca ![]() , atunci exista indoieli ca erorile ar fi corelate;
, atunci exista indoieli ca erorile ar fi corelate;
5. daca ![]() , atunci erorile sunt negativ corelate.
, atunci erorile sunt negativ corelate.
In exemplul nostru, numarul de exogene veritabile in model este (m=1) si dispunem de T=15 observatii.
Tabela D-W furnizeaza valorile d1=1,08 si d2=1,36 la pragul de semnificatie a=0,05.
Deoarece ![]() , suntem intr-o situatie de indecizie, nu putem sa
spunem ca erorile
, suntem intr-o situatie de indecizie, nu putem sa
spunem ca erorile ![]() sunt corelate.
sunt corelate.
II. In tabelul urmator sunt date, pentru perioada 1985-2002:
volumul investitiilor in agricultura, yt;
produsul intern brut agricol, x1t;
indicele volumului importurilor pentru agricultura, x2t.
|
Anul t |
Investitii in agricultura yt |
Produsul intern brut agricol x1t |
Indicele volumului importurilor pentru agricultura x2t |
|
1985 |
85,2 |
563,8 |
90,6 |
|
1986 |
90,2 |
594,7 |
91,7 |
|
1987 |
96,6 |
635,7 |
92,9 |
|
1988 |
112,0 |
688,1 |
94,5 |
|
1989 |
124,5 |
753,0 |
97,2 |
|
1990 |
120,8 |
796,3 |
100,0 |
|
1991 |
131,5 |
868,5 |
104,2 |
|
1992 |
146,2 |
935,5 |
109,8 |
|
1993 |
140,8 |
982,4 |
116,3 |
|
1994 |
160,0 |
1063,4 |
121,3 |
|
1995 |
188,3 |
1171,1 |
125,3 |
|
1996 |
220,0 |
1306,6 |
133,1 |
|
1997 |
214,6 |
1412,9 |
147,7 |
|
1998 |
190,9 |
1528,8 |
161,2 |
|
1999 |
243,0 |
1702,2 |
170,5 |
|
2000 |
303,3 |
1899,5 |
181,5 |
|
2001 |
351,5 |
2127,6 |
195,4 |
|
2002 |
386,2 |
2368,5 |
217,4 |
Se cere:
1. Determinarea legaturii dintre investitii, PIB si volumul importurilor;
2. Testarea autocorelatiei erorilor;
3. Daca exista autocorelatie, cum se pot inlatura efectele acesteia?
Rezolvare:
Studierea legaturii dintre variabilele economice amintite se poate efectua cu modelul de regresie multipla:
![]()
Aplicarea MCMMP conduce la urmatoarea
estimare a modelului: ![]()
Coeficientul de corelatie multipla are valoarea calculata: R2=0,98
2. Dupa calcularea reziduurilor estimate, ![]() , statistica Durbin-Watson este:
, statistica Durbin-Watson este: ![]() . Conform tabelei D-W, pentru α=5%, T=18 observatii
si m=2 variabile exogene veritabile, rezulta: d1=1,05>
. Conform tabelei D-W, pentru α=5%, T=18 observatii
si m=2 variabile exogene veritabile, rezulta: d1=1,05>![]() , ceea ce conduce la concluzia ca erorile sunt corelate
pozitiv.
, ceea ce conduce la concluzia ca erorile sunt corelate
pozitiv.
3. Pentru a inlatura efectele autocorelatiei erorilor, se procedeaza astfel:
- scriem dependenta dintre variabile
(1) ![]() , pentru momentul t-1:
, pentru momentul t-1:
(2) ![]()
- inmultim (2) cu ρ si efectuam scaderea (1)-(2):
![]()
cautam o estimatie a coeficientului ρ. Observam ca ρ este coeficientul variabilei yt-1 in relatia anterioara. Efectuam o regresie cu MCMMP pe ultima ecuatie, fara sa tinem cont de relatiile dintre coeficienti, adica pe ecuatia:
![]()
unde a0=a(1- ρ) , a1=b, a2=-bρ,
a3=c, a4=-cρ si ![]()
Efectuind calculele, obtinem:
![]() Estimatia gasita pentru coeficientul ρ
este
Estimatia gasita pentru coeficientul ρ
este ![]()
cu ajutorul estimatiei gasite, transformam variabilele modelului initial pentru o noua regresie:
|
Anul |
|
|
|
|
1985 |
|
|
|
|
1986 |
30,56 |
200,04 |
28,28 |
|
1987 |
33,46 |
219,41 |
28,71 |
|
1988 |
44,38 |
243,11 |
29,47 |
|
1989 |
46,10 |
271,33 |
31,05 |
|
1990 |
33,68 |
269,70 |
31,96 |
|
1991 |
46,94 |
311,09 |
34,20 |
|
1992 |
54,15 |
327,55 |
36,86 |
|
1993 |
38,46 |
327,55 |
39,44 |
|
1994 |
61,44 |
375,72 |
39,89 |
|
1995 |
76,30 |
426,72 |
40,39 |
|
1996 |
88,19 |
486,83 |
45,39 |
|
1997 |
60,60 |
498,28 |
54,53 |
|
1998 |
40,68 |
539,77 |
57,81 |
|
1999 |
109,37 |
632,04 |
57,66 |
|
2000 |
133,20 |
707,96 |
62,15 |
|
2001 |
139,19 |
797,95 |
68,35 |
|
2002 |
140,15 |
879,18 |
80,62 |
Observatie:
Pentru a evita eliminarea primei valori din
sirul de observatii, prin trecerea la diferente, se pot folosi
transformarile: ![]() ,
, ![]() ,
, ![]()
se aplica MCMMP ecuatiei:
![]() , si rezulta:
, si rezulta:
![]()
Coeficientul de corelatie multipla este acum R2=0,88
iar statistica Durbin-Watson ![]() . Testul de independenta conduce acum la concluzia
ca erorile sunt independente, deoarece:
. Testul de independenta conduce acum la concluzia
ca erorile sunt independente, deoarece:
4-d2=2,47>![]() =1,54>d2=1,53
=1,54>d2=1,53
2. Ipoteza de normalitate a erorilor
Unele proprietati ale estimatorilor nu depind de
normalitatea erorilor. De exemplu, distributiile asimptotice ale
estimatorilor necesita doar existenta primelor doua momente
(media si dispersia) ale erorilor ![]() si nu in mod
obligatoriu ca
si nu in mod
obligatoriu ca ![]() sa urmeze o lege
normala. Acest lucru nu este insa valabil pe esantioane mici.
Testarea ipotezelor si intervalele de incredere nu mai au aceleasi
proprietati daca legea de distributie a erorilor nu este
legea normala. Pentru a caracteriza deviatiile de la legea
normala se utilizeaza doi coeficienti:
sa urmeze o lege
normala. Acest lucru nu este insa valabil pe esantioane mici.
Testarea ipotezelor si intervalele de incredere nu mai au aceleasi
proprietati daca legea de distributie a erorilor nu este
legea normala. Pentru a caracteriza deviatiile de la legea
normala se utilizeaza doi coeficienti:
a) coeficientul de asimetrie, calculat prin raportul:
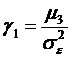
unde: ![]() este momentul centrat
de ordinul 3. Daca
este momentul centrat
de ordinul 3. Daca ![]() , atunci seria de date este deplasata spre dreapta
fata de legea normala, iar daca
, atunci seria de date este deplasata spre dreapta
fata de legea normala, iar daca ![]() , exista o deviere spre stanga.
, exista o deviere spre stanga.
b) coeficientul de aplatizare, calculat prin raportul:
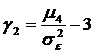
O valoare pozitiva pentru ![]() indica faptul
ca distributia este mai putin aplatizata decat
distributia normala, in timp ce o valoare
indica faptul
ca distributia este mai putin aplatizata decat
distributia normala, in timp ce o valoare ![]() caracterizeaza o
distributie mai aplatizata decat cea normala.
caracterizeaza o
distributie mai aplatizata decat cea normala.
Aceste deviatii afecteaza testele si intervalele de incredere ale estimatorilor. Studiul teoretic al acestor deviatii este complex. Pentru a obtine teste si intervale de incredere mai robuste, in practica se procedeaza astfel:
1.
Se efectueaza o regresie cu
metodele uzuale si se determina o estimatie a reziduurilor ![]() .
.
2. Se examineaza cele T reziduuri estimate si se repereaza cele a caror valoare absoluta este foarte mare.
3. Se elimina din seria de date observatiile corespunzatoare acestor erori foarte mari sau se corecteaza aceste observatii astfel ca sa se ajunga la valori cat mai normale ale erorilor.
4.
Se efectueaza o noua
regresie pe esantionul corectat. Proprietatile estimatorilor
obtinuti vor depinde de regula adoptata in etapa
anterioara. De exemplu, se poate adopta regula de a respinge sau corecta
observatiile corespunzatoare reziduurilor a caror valoare
absoluta ![]() este mai mare decat de
trei ori media erorilor absolute.
este mai mare decat de
trei ori media erorilor absolute.
3. Ipoteza de heteroscedasticitate
Sa presupunem, deci, ca desi ![]() sunt independente, dispesia erorilor
sunt independente, dispesia erorilor ![]() variaza in
functie de t. In acest caz,
estimatorii obtinuti sunt inca nedeplasati. Dar, momentele
centrate de ordinul doi nemaifiind constante se comite o eroare de calcul a
ecartului-tip al estimatorilor. Se poate evalua deplasarea in estimatia
lui
variaza in
functie de t. In acest caz,
estimatorii obtinuti sunt inca nedeplasati. Dar, momentele
centrate de ordinul doi nemaifiind constante se comite o eroare de calcul a
ecartului-tip al estimatorilor. Se poate evalua deplasarea in estimatia
lui ![]() . Aceasta deplasare depinde de natura si
importanta heteroscedasticitatii, adica de sirul de
valori
. Aceasta deplasare depinde de natura si
importanta heteroscedasticitatii, adica de sirul de
valori ![]() . Deplasarea este nula daca sunt realizate
relatiile urmatoare:
. Deplasarea este nula daca sunt realizate
relatiile urmatoare:
(1) ![]() ;
;
(2) 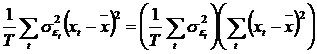 .
.
Aceste relatiile sunt realizate atunci cand nu exista nicio
legatura sistematica intre ![]() si
si ![]() .
.
Homoscedasticitatea erorilor se admite in seriile cronologice atunci cand ordinul de marime al variabilelor este apropiat pentru diverse observatii. Dar, in studiul datelor micro-economice, variabilele pot avea ordine de marime foarte diferite. Acest fapt conduce la erori de estimare importante pentru coeficientii unui model econometric.
Daca putem evalua varianta erorilor ![]() atunci, in loc sa
determinam parametrii din conditia ca suma patratelor erorilor
sa fie minima, acestia pot fi determinati din conditia
ca
atunci, in loc sa
determinam parametrii din conditia ca suma patratelor erorilor
sa fie minima, acestia pot fi determinati din conditia
ca 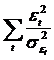 sa fie
minima.
sa fie
minima.
Pentru modelul elementar ![]() , estimatorii
, estimatorii
![]() si
si ![]() vor fi cei care minimizeaza expresia
vor fi cei care minimizeaza expresia 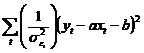
In cazul in care ![]() (dispersiile
reziduurilor) variaza proportional cu valorile variabilei exogene, se
poate pune conditia ca
(dispersiile
reziduurilor) variaza proportional cu valorile variabilei exogene, se
poate pune conditia ca 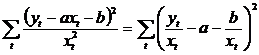 sa fie
minima.
sa fie
minima.
3.1. Experienta de calcul
Ne propunem sa studiem legatura dintre volumul investitiilor si suprafata cultivata. Pe un esantion de 30 de intreprinderi agricole s-au obtinut urmatoarele date:
|
Suprafata (ha) |
Cheltuielile de investitii (RON) |
|||||
|
100 |
75,6 |
75,6 |
77,4 |
78,3 |
80,1 |
81 |
|
200 |
80,1 |
81,9 |
83,7 |
83,7 |
84,6 |
84,6 |
|
300 |
85,5 |
88,2 |
89,1 |
92,7 |
92,7 |
94,5 |
|
400 |
92,7 |
95,4 |
98,1 |
101,7 |
103,5 |
105,3 |
|
500 |
104,4 |
106,2 |
108,9 |
112,5 |
117,9 |
117,9 |
Aplicand MCMMP pe intregul esantion cu modelul elementar ![]() , obtinem:
, obtinem:
![]() si
si ![]() .
.
Dorim sa testam ipoteza de homoscedasticitate a erorilor. In acest scop efectuam doua regresii separate, una pe primele 12 observatii, alta pe ultimele 12 (valorile lui X fiind ordonate crescator).
Fie SPE1 si SPE2 suma patratelor erorilor relative la cele doua regresii.
Regresia lui Y in raport cu X pentru primele 12 observatii, conduce la:
![]() si
si ![]() ;
; ![]() ,
,
iar regresia pe ultimele 12 observatii da:
![]() si
si ![]() ;
; ![]() .
.
In cazul in care erorile ar fi distribuite normal si
homoscedastice, variabilele aleatoare ![]() , respectiv
, respectiv ![]() ar trebui sa
urmeze fiecare o distributie hi-patrat
cu (T-d-k-p) grade de libertate, unde
T este numarul de
observatii, d este numarul
de observatii omise (in cazul nostru d=6),
k este numarul de
observatii luat in fiecare regresie separata, iar p este numarul parametrilor de
estimat. In exemplul nostru T-d-k-p=10.
In aceste conditii, variabila aleatoare
ar trebui sa
urmeze fiecare o distributie hi-patrat
cu (T-d-k-p) grade de libertate, unde
T este numarul de
observatii, d este numarul
de observatii omise (in cazul nostru d=6),
k este numarul de
observatii luat in fiecare regresie separata, iar p este numarul parametrilor de
estimat. In exemplul nostru T-d-k-p=10.
In aceste conditii, variabila aleatoare 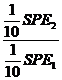 are o distributie
Fisher cu 10 si respectiv 10 grade de libertate (F10,10). Cu datele calculate, obtinem
are o distributie
Fisher cu 10 si respectiv 10 grade de libertate (F10,10). Cu datele calculate, obtinem ![]() . Din tabelele distributiei Fischer-Snedecor, la pragul
de semnificatie a=0,05 gasim Ftab=2,97.
Deoarece Fcalc=51,01>Ftab=2,97
se admite ipoteza de heteroscedasticitate a erorilor.
. Din tabelele distributiei Fischer-Snedecor, la pragul
de semnificatie a=0,05 gasim Ftab=2,97.
Deoarece Fcalc=51,01>Ftab=2,97
se admite ipoteza de heteroscedasticitate a erorilor.
Daca presupunem acum ca varianta erorilor ![]() este
proportionala cu patratul valorilor variabilei exogene,
adica
este
proportionala cu patratul valorilor variabilei exogene,
adica ![]() , l fiind o constanta nenula,
atunci efectele heteroscedasticitatii pot fi corectate prin
transformarea modelului. Impartind fiecare termen al ecuatiei de regresie prin xt, rezulta:
, l fiind o constanta nenula,
atunci efectele heteroscedasticitatii pot fi corectate prin
transformarea modelului. Impartind fiecare termen al ecuatiei de regresie prin xt, rezulta:
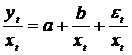
sau ![]() , unde:
, unde: ![]()
![]() si
si ![]()
Se observa ca 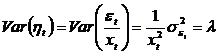
Prin urmare, modelul transformat are erorile ![]() homoscedastice,
deoarece dispersia lor este independenta de timp. Efectuand regresia pe
modelul transformat, rezulta:
homoscedastice,
deoarece dispersia lor este independenta de timp. Efectuand regresia pe
modelul transformat, rezulta:
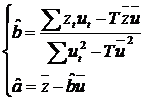
Revenind in variabilele initiale obtinem:
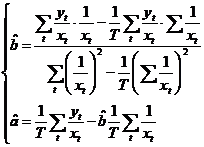
Efectuand calculele, rezulta:
![]() ;
; ![]() ;
; ![]() , adica:
, adica:
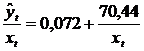 sau
sau ![]() .
.
Sa remarcam faptul ca panta dreptei de regresie (dupa corectarea heteroscedasticitatii) este mai mica decat cea obtinuta inaintea corectarii.
Ipoteza de independenta a erorilor in raport cu varibilele exogene
Se stie ca sub aceasta ipoteza fundamentala
estimatorii obtinuti au proprietati optimale
(nedeplasati, cu varianta minimala). Cand ipoteza nu mai
este satisfacuta aceste proprietati nu mai sunt valabile.
Cu cat coeficientul de corelatie liniara (![]() ) dintre
) dintre ![]() si
si ![]() este mai mare, cu atat
deplasarea estimatorilor va fi mai mare. In astfel de cazuri este de preferat
sa se aleaga un alt model econometric pentru studierea legaturii
dintre variabile.
este mai mare, cu atat
deplasarea estimatorilor va fi mai mare. In astfel de cazuri este de preferat
sa se aleaga un alt model econometric pentru studierea legaturii
dintre variabile.
La fel trebuie procedat si atunci cand se constata ca varianta erorilor nu este finita.
5. Ipoteza referitoare la faptul ca variabilele modelului sunt observate fara eroare
Atunci cand variabilele care apar in model nu sunt variabile observate fara eroare, va exista o corelatie intre reziduuri si exogenele din model.
In acest caz, pentru a obtine estimatori convergenti, s-a dezvoltat o metoda de estimare speciala, numita "metoda variabilelor instrumentale", pe care o prezentam mai jos.
Fie modelul liniar general:
![]() , t=1, 2, ,T,
, t=1, 2, ,T,
care, cu
notatiile obisnuite, se scrie in forma matriciala Y=Xa+e. Notam cu ![]() si
si ![]() valorile reale
(necunoscute acum pentru ca observatiile Y si X contin
erori!) ale variabilelor din model.
valorile reale
(necunoscute acum pentru ca observatiile Y si X contin
erori!) ale variabilelor din model.
Putem scrie ca ![]() ,
, ![]() , unde m si g sunt variabile aleatoare. Vom presupune ca m si g satisface ipotezele fundamentale (medie zero, varianta
finita, independente).
, unde m si g sunt variabile aleatoare. Vom presupune ca m si g satisface ipotezele fundamentale (medie zero, varianta
finita, independente).
Inlocuind X si Y prin expresiile lor, obtinem
modelul ![]() , unde
, unde ![]() . Aceasta arata ca in modelul initial, Y=Xa+e , reziduurile e sunt corelate cu X prin
intermediul lui g
. Aceasta arata ca in modelul initial, Y=Xa+e , reziduurile e sunt corelate cu X prin
intermediul lui g
Presupunem acum ca se cunosc alte p variabile exogene Zi, i=1,2,,p necorelate cu m g si h, deci necorelate cu e
Acest lucru inseamna ca ![]() , i=1,2,,p. Consideram modelul initial Y=Xa+e scris sub forma:
, i=1,2,,p. Consideram modelul initial Y=Xa+e scris sub forma:
(1) ![]() ,
,
unde 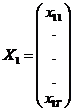 ,
,  ,,
,, 
Inmultim, succesiv, ecuatia (1) cu Z1, Z2, Zp si aplicam operatorul de medie E fiecarei ecuatii. Se obtine sistemul:
(2) 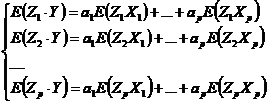
Metoda de estimare VI (variabilelor instrumentale) consta in a
lua ca estimatori ![]() exact solutiile
sistemului de ecuatii (2), in care sperantele matematice sunt
inlocuite cu momentele empirice corespunzatoare:
exact solutiile
sistemului de ecuatii (2), in care sperantele matematice sunt
inlocuite cu momentele empirice corespunzatoare:
![]() , i=1,2,,p
, i=1,2,,p
![]() , i,j=1,2,,p
, i,j=1,2,,p
Daca notam:
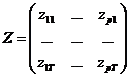 si
si  sistemul (2)
transformat se scrie sub forma matriciala:
sistemul (2)
transformat se scrie sub forma matriciala: ![]() , iar pentru ca
, iar pentru ca ![]() este inversabila,
obtinem estimatorul:
este inversabila,
obtinem estimatorul:
![]() .
.
Sa observam similitudinea cu estimatorii obtinuti prin MCMMP:
1. MCMMP obisnuita: ![]()
2. MCMMP generalizata: ![]()
3. metoda VI: ![]() .
.
Se trece de la 1. la 2. inlocuind ![]() prin
prin ![]() .
.
Se trece de la 1. la 3. inlocuind ![]() prin
prin ![]() .
.
Cunoasterea primei formule permite exprimarea celorlalte doua.
Estimatorul ![]() obtinut prin
metoda VI este un estimator deplasat pentru a,
dar converge in probabilitate catre a
pentru T suficient de mare.
obtinut prin
metoda VI este un estimator deplasat pentru a,
dar converge in probabilitate catre a
pentru T suficient de mare.
Pentru a putea utiliza metoda VI trebuie gasite atatea variabile instrumentale cate exogene contine modelul. Aceste variabile instrumentale trebuie sa fie necorelate cu reziduurile, dar puternic corelate cu exogenele modelului. Aceste restrictii limiteaza alegerea variabilelor instrumentale si, prin urmare, metoda VI nu este o metoda generala de estimare.
5.1. Experienta de calcul
Consideram o ancheta pe bugetele de familie pentru a studia consumul dintr-un anumit produs. Ancheta cuprinde un esantion de T familii. Facem urmatoarele notatii:
y1t: cheltuielile totale ale familiei t;
y2t: cheltuielile relative la produsul studiat;
Vt: veniturile familiei t;
si scriem ecuatiile:
(1) ![]()
(2) ![]()
Ne propunem sa exprimam cheltuielile relative la produsul
studiat in functie de cheltuielile totale. Din ecuatia (1) avem
ca ![]() si inlocuind in
(2), rezulta:
si inlocuind in
(2), rezulta:
![]()
sau, punand ![]() :
:
(3) ![]() .
.
Sa observam ca ![]() este corelat cu y1t prin intermediul lui e1t
este corelat cu y1t prin intermediul lui e1t
Vom estima a si b din ecuatia (3) introducand o variabila instrumentala.
Fie VDt venitul declarat de familia t. Este evidenta corelatia puternica dintre variabilele VDt si Vt.
Dimpotriva, venitul declarat VDt
nu este corelat cu ![]() , care este ecartul intre cheltuielile totale si
veniturile familiei t. Rezulta
ca VDt nu va fi
corelat cu
, care este ecartul intre cheltuielile totale si
veniturile familiei t. Rezulta
ca VDt nu va fi
corelat cu ![]() . Utilizam venitul declarat ca variabila
instrumentala.
. Utilizam venitul declarat ca variabila
instrumentala.
Pentru simplificarea calculelor, centram variabilele din model:
![]() , t=1,2,,T
, t=1,2,,T
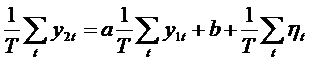
![]()
(4) ![]()
Daca aplicam MCMMP ecuatiei (4), obtinem estimatorul:
(5). 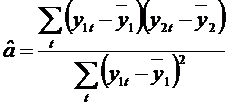
Folosim insa metoda variabilelor instrumentale. Pentru aceasta,
consideram variabila instrumentala centrata ![]() . Inmultind ecuatia (4) cu variabila
instrumentala centrata si aplicand operatorul de medie E, rezulta:
. Inmultind ecuatia (4) cu variabila
instrumentala centrata si aplicand operatorul de medie E, rezulta:
![]() .
.
Dar, cum ![]() si VDt nu sunt corelate,
inseamna ca
si VDt nu sunt corelate,
inseamna ca ![]() , iar acum inlocuind E
cu media empirica, obtinem:
, iar acum inlocuind E
cu media empirica, obtinem:
![]()
![]() ,
,
de unde:
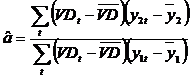 .
.
Am obtinut practic estimatorul (5) in care variabila ![]() s-a inlocuit cu
variabila instrumentala
s-a inlocuit cu
variabila instrumentala ![]() atat la
numarator, cat si la numitor.
atat la
numarator, cat si la numitor.
BIBLIOGRAFIE
1. Andrei, T. Statistica si econometrie, Editura Economica, Bucuresti, 2004
2. Cenusa, Ghe. (coord.) Matematici pentru economisti, Editura CISON, Bucuresti, 2000
3. Chow, G. Econometrics, McGraw Hill, New York, 1989
Dobrescu, E. Tranzitia in Romania-Abordari econometrice, Editura Economica, Bucuresti, 2002
5. Gheroghita, M. Modelarea si simularea proceselor economice, Editura ASE, Bucuresti, 2001
6. Giraud, R. - Econometrie, Economica, 49 rue Hericart, Paris, 1990
7. Gourieroux, C. Statistique et Modeles Econometriques,
Monfort, A. Economica, Paris, 1989
8. Gujarati, R.N. Essentials of Econometrics, McGraw Hill, New York, 1998
9. Isaic-Maniu, Al. Statistica pentru managementul
Mitrut, C. afacerilor, Editura Economica, 1995
Voineagu, V.
10. Malinvaud, E. Methodes statistiques de l'econometrie, Dunod, Paris, 1978
11. Onicescu, O. Incertitudine si modelare economica
Botez, M. (Econometrie informationala), Editura Stiintifica si Enciclopedica, Bucuresti, 1985
12. Pecican, E.S. Econometria pentru economisti; Econometrie-teorie si aplicatii,
Editura Economica, Bucuresti, 2003
13. Pecican, E.S. Econometrie, Editura All, Bucuresti, 1994
1 Tasnadi, Al. Econometrie, Editura A.S.E., 2001
15. Tasnadi, Al. Econometrie - proiect, Editura A.S.E.,
Cretu, A. 2003
Peptan, E.
16. Tanasoiu, O. Modele econometrice, Editura A.S.E.,
Pecican, E.S. 2001
Iacob, A.
17. Tanasoiu, O. Econometrie-studii de caz, Editura A.S.E., 1998
18. Tanasoiu, O. Econometrie aplicata, Editura Arteticart,
Iacob, A. Bucuresti, 1999
19. www.asecib.ase.ro/soft.htm
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||
|
|||
Lucrari pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








