
| Afaceri | Agricultura | Comunicare | Constructii | Contabilitate | Contracte |
| Economie | Finante | Management | Marketing | Transporturi |
Economie
|
|
Qdidactic » bani & cariera » economie Modelul input-output al cresrerii economice |
Modelul input-output al cresrerii economice
Modelul input-output al cresrerii economice
Acest tip de model prezinta un dublu avantaj fata de cele anterioare:
- Pe de o parte, au o arie mult mai larga de informare teoretica si metodologica;
- Pe de alta parte, pun in discutie o problema teoretica si practica deosebit de complexa si anume aceea a interdependentelor dintre compartimentele structurilor din cadrul fiecarei economii nationale.
Exemplul cel mai reprezentativ in aceasta privinta il constituie modelul input-output (balanta legaturilor dintre ramuri), elaborat de W. Leontief.
Meritul principal al modelelor economice structurale consta in faptul ca incearca sa cuantifice, cu ajutorul unor coeficienti, intensitatea fluxurilor intre ramurile economiei nationale, oferind elemente valoroase pentru determinarea conditiilor care se cer in vederea respectarii unor proportii rationale in functionarea normala a complexului economic.
In acest model productia fiecarei ramuri, notata X, (i = 1, 2,, n) este descompusa pe elementele de destinatie: consum pentru productia proprie si pentru productia altor ramuri. Daca notam x;j Q = 1, 2,, n) partea din productia ramurii i care se consuma productiv, intr-o anumita perioada, in ramura j, atunci productia ramurii i se poate scrie sub forma unei ecuatii:
XI= xi1+xi2+.+xin
Pentru i = 1, 2, , n se obtine un sistem de ecuatii care caracterizeaza relatiile de productie-consum din economie:
X1=x11+x12+.+x1n
X2=x21+x22+.+x2n
Xi=xi1+xi2+.+xij+.+xin
Xn=xn1+xn2+.+xnn
Elementele xij se numesc fluxuri interramuri. Cantitatea din productia ramurii i absorbita de ramura j, impartita la productia totala a ramurii j, este descrisa cu simbolul aij si este numita coeficientul intrarilor productiei din ramura i in ramura j.
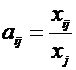
unde:
Xj- productia totala a ramurii j.
Considerand ca numarul ramurilor cuprinse in balanta este n, deci i=j, modelul matematic al sistemului inchis al sistemului poate fi prezentat de urmatorul sistem de ecuatii:
a11X1+a12X2+.+a1nXn=X1
a21X1+a22X2+.+a2nXn=X2
an1X1+an2X2+.+annXn=Xn
sau, sub forma matriceala:
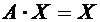
In baza celor de mai sus, este evident ca:
- Suma coeficientilor dintr-o coloana (dupa i=1; n) este egala cu 1
![]() ;
;
- Suma totalurilor pe coloane (intrari) este egala cu suma totala pe linii (iesiri) (dupa i=1; j=1; n):
![]()
sau:
(1-a11)X1-a12X2-.-a1nXn=0
|
-a21X1-(1-a22)X2-.-a2nXn=0
-an1X1-an2X2-.-(1-annXn)=0
sau:
(1-A)X=0
Prin rezolvarea sistemului de ecuatii de mai sus se obtine proportiile dintre necunoscutele X1,X2,.,Xn (productiile globale ale ramurilor). Pentru echilibrarea sistemului inchis, suma livrarilor (iesirilor) fiecarei ramuri catre celelalte trebuie sa fie egala cu suma primirilor (intrarilor) de la celelalte.
Volumul productiei fiecarei ramuri se poate exprima in unitati naturale sau valorice si ca urmare vom avea: fie balanta in expresie naturala, fie in expresie valorica.
Rolul cel mai important intr-un tablou input-output revine coeficientilor intrarilor (aij) pentru ca in functie de ei se poate stabilii, pe baze aproape de realitate, influentele productiei unei ramuri asupra altora cu care au relatii de "intrare-iesire".
Iata, deci, un exemplu de Model Input-Output, intr-o economie de tip inchis care - presupunem - are trei sectoare:
|
Ramuri Produse |
Agricultura |
Industrie |
Tertiar |
Consum final |
Productie totala |
|
Agricultura |
15 |
50 |
20 |
45 |
130 |
|
Industrie |
50 |
50 |
25 |
65 |
160 |
|
Tertiar |
10 |
50 |
50 |
50 |
190 |
|
Cumparari Intermediare |
75 |
150 |
95 |
160 |
|
|
Valoarea adaugata |
55 |
40 |
65 |
160 |
|
|
Intrari totale |
130 |
190 |
160 |
|
480 |
Pe orizontala avem 'IESIRI CATRE ALTE RAMURI'
Iata, de pilda, lectura liniilor (randurilor). Exemplul de utilizare a productiei agricole.
Agricultura a produs 130 u.m. de produse agricole (output). 15 u.m. reprezinta autoconsumul ramurii agricultura (de pilda, nutret pentru animale). 50 u.m. sunt output orientat spre industrie si sunt consumate productiv acolo (laptele pentru producerea inghetatei). 20 u.m. sunt iesiri (output) pentru sectorul serviciilor ca factori de productie de origine agricola (restaurantele folosesc carne, unt, etc.). 45 u.m. sunt iesiri spre populatie (consumul familial de produse agricole).
Pe verticala avem 'INTRARI DE LA ALTE RAMURI'.Ilata, aici, lectura coloanelor. Exemplul de cumparari ale ramurii industrie.
Industria (agro-alimentara) utilizeaza 50 u.m. produse agricole intrate de la agricultura (laptele pentru inghetata). 50 u.m. produse (industriale) vor fi utilizate pentru autoconsum (panza pentru camasi). 50 u.m. vor fi intrari de la sectorul tertiar (transport, comert, marketing, etc.). Industria a utilizat 150 u.m. sub forma de consumuri intermediare diverse (inputuri de la alte ramuri) pentru a obtine o productie proprie de 190 u.m., din care 40 u.m. reprezinta valoarea adaugata.
In acest tablou, consumul final apare ca cea de a (n +1) coloana, iar valoarea adaugat ca cea de a (n + 1) linie. In realitate, cea de a (n + 1) coloana si cea de a (n + 1) linie nu au acelasi statut ca si cele n linii si n coloane. Cele n linii si n coloane descriu (singure) industriile cu tehnologiile date: agricultura industrie, tertiar.
De aici a venit ideea lui Leontief de a trasa un model deschis, cu coeficienti tehnici reprezentand cantitatea unui input necesara pentru a obtine o unitate de output.
|
Ramuri produse |
Agricultura |
Industrie |
Tertiar |
|
Agricultura |
15/130 |
50/130 |
20/130 |
|
Industrie |
50/190 |
150/190 |
25/190 |
|
Tertiar |
10/160 |
50/160 |
50/160 |
Leontief a emis ipoteza ca acesti coeficienti tehnici sunt putini sensibili la variatiile pe termen scurt. Ei pot, in aceste conditii sa serveasca la calculele matriciale menite sa fundamenteze deciziile de planificare a economiei nationale.
1. Care este autoconsumul unei ramuri?
In exemplul nostru, coeficientul a11 = 151130, arata ca 15 u.m. din productia agricola se utilizeaza in ramura agriculturii pentru a obtine o productie totala a ramurii de 130 u.m.
2. Care este dependenta unei ramuri in raport cu alta?
Care sunt 'locurile inguste', 'strangularile' din economie? Nu ne serveste la nimic dorinta de a spori productia unei ramuri, daca alte ramuri nu pot sa furnizeze factorii de productie necesari. De asemenea, nu putem spori produc~ia unei ramuri, daca iesirile spre alte ramuri de destinatie nu permit acest lucru.
3. Care sunt consecintele modificarii activitatii unei ramuri asupra altora?
Unele ramuri economice au un efect de impulsionare asupra altora.
4. Daca se relanseaza activitatea economica, in special consumul final al menajelor, ce repercusiuni se vor produce asupra productiei, ocuparii, importurilor?
Intr-o economie deschisa, relansarea productiei intr-o ramura, sau mai multe, care consuma produse importate, va genera probleme de natura modificarii acestor importuri. Daca ele nu se pot modifica corespunzator, nici dorinta de sporire a productiei ramurilor respective nu va deveni realitate. La fel, productia unor ramuri a caror productie este destinata exporturilor, va depinde in mare masura - de posibilitatile de export.
Modelele input-output sunt deosebit de utile in procesul cresterii economice si chiar al planificarii, intrucat ofera posibilitatea construirii de 'scenarii alternative si comparative, fiecare dintre ele raspunzand unui ansamblu diferit de ipoteze referitoare la structura cererii finale, schimbarilor in valoarea coeficientilor de input incorporati in diversi vectori coloana ai coeficientilor fluxurilor de capital, sau alte combinatii.
Printre limitele acestor modele structurale retinem:
- Nu ierarhizeaza ramurile economiei nationale dupa importanta lor. Aici toate ramurile sunt egale ca importanta, ori in politica economica aplicata situatia este alta. De aceea, pentru a utiliza balanta legaturilor ramurilor ca instrument de planificare, trebuie introduse in model, ca variabile exogene, optiunile de politica economica. Oricum, prin balanta se pot verifica daca sunt sau nu sunt bine fundamentate optiunile de dezvoltare 'exogene'.
- Modelele input-output nu pot surprinde corespunzator toate actiunile speculative din domeniul financiar;
- Balanta legaturilor dintre ramuri este mai mult un model de analiza postfactum a realitatii economice si mai putin un instrument de previziune, de anticipare.
Intocmite cu mare regularitate, tablourile input-output la nivelul economiei nationale pot furniza pretioase informatii asupra tendintelor (cel putin interne) de evolutie a vietii economice.
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||
|
|||
Analize pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








