
| Afaceri | Agricultura | Comunicare | Constructii | Contabilitate | Contracte |
| Economie | Finante | Management | Marketing | Transporturi |
Economie
|
|
Qdidactic » bani & cariera » economie Globalizarea pietelor financiare |
Globalizarea pietelor financiare
Globalizarea pietelor financiare
Cum era de asteptat, nu exista o definitie global acceptata a fenomenului
globalizarii, dar o expresie sintetica ar suna in felul urmator:
'Globalizarea consta in intensificarea cantitativa si calitativa a
tranzactiilor care depasesc limitarea impusa de granite, concomitent cu
expansiunea spatiala a acestora' (Ulrich MENZEL).
Sigur ca nu este vorba despre o definitie exhaustiva dar, cel putin la nivel macroeconomic, globalizarea se poate defini ca un proces prin care se asigura o interdependenta sporita si o integrare a diferitelor economii din lume.
Exista opinii divergente asupra efectelor
acestui fenomen, specialisti de renume penduland intre a-l considera fie un rau
necesar care conduce la cresterea competitiei intre operatorii din orice piata,
la dezvoltarea comertului si a investitiilor directe, fie intre un
'inceput al sfarsitului' pentru economiile nationale.
Cert este insa ca inegalitatile si diferentele dintre potentialul de crestere
al diferitelor piete reprezinta deopotriva cauza si stimulentul fenomenului de
globalizare.
Daca ne referim in mod direct la industria
serviciilor financiare, este firesc ca din ce in ce mai multi operatori din
Europa Occidentala decid sa isi extinda activitatea in Europa de Est si in tarile
membre ale CSI (Comunitatea Statelor Independente) in conditiile in care, in
statele dezvoltate potentialul industriei este aproape in totalitate exploatat.
Ritmuri de crestere de ordinul a 15-20%, cum adesea putem observa in domeniul
bancar si al asigurarilor din tarile Europei de Est sunt poate de domeniul
fantasticului in tari precum Germania sau Austria.
Potentialul pietelor din fostul bloc comunist nu mai este neglijat de mult
timp, aproape toate marile corporatii, incluzand aici si gruparile bancare si
de asigurari, intrand deja pe aceste piete sau urmand sa o faca in scurt timp.
Rusia, Ucraina, Belarus sau Kazahstan au devenit din zone necartografiate in
strategiile furnizorilor de servicii financiare in piete de mare viitor.
|
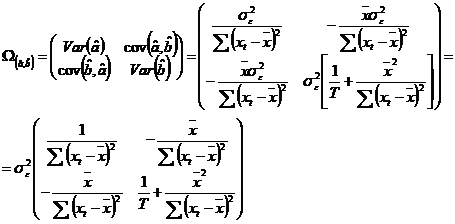
Se remarca faptul ca ![]() contine pe
contine pe ![]() , adica varianta lui
, adica varianta lui ![]() care este
necunoscuta. Se pune deci problema de a obtine o estimatie
pentru
care este
necunoscuta. Se pune deci problema de a obtine o estimatie
pentru ![]() , adica o estimatie pentru
, adica o estimatie pentru ![]() . Notam aceasta estimatie cu
. Notam aceasta estimatie cu ![]() .
.
2.3.2. Determinarea unui estimator nedeplasat pentru varianta erorilor
Utilizand estimatorii ![]() si
si ![]() putem calcula estimatia
variabilei endogene yt,
notata
putem calcula estimatia
variabilei endogene yt,
notata ![]() (se mai
numesc si valori ajustate ale variabilei endogene):
(se mai
numesc si valori ajustate ale variabilei endogene): ![]()
Atunci diferenta dintre yt
si ![]() este un estimator
pentru eroarea
este un estimator
pentru eroarea ![]() . Notam
. Notam ![]() . Avem ca
. Avem ca ![]() . Remarca: deoarece
. Remarca: deoarece
![]() si
si ![]() converg in
probabilitate catre a si b, distributia lui
converg in
probabilitate catre a si b, distributia lui ![]() converge in
probabilitate catre distributia lui
converge in
probabilitate catre distributia lui ![]() (distributie
normala, conform I2).
(distributie
normala, conform I2).
Stim ca ![]() si inlocuind
obtinem:
si inlocuind
obtinem:
![]() .
.
iar prin ridicare la patrat:
![]()
Insumam dupa t=1,2,,T si impartim la T:
![]() .
.
Dar: 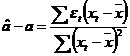 , si
, si
![]()
pentru ca 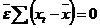 .
.
Inlocuind, rezulta:
 .
.
Notam cu ![]() dispersia erorilor
fata de media lor si cum ea este o variabila aleatoare, ii
calculam media
dispersia erorilor
fata de media lor si cum ea este o variabila aleatoare, ii
calculam media ![]() :
:
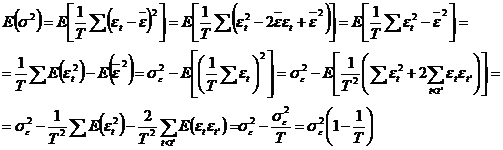
Aplicand acum operatorul de medie in relatia:
![]() ,
,
si tinind cont de expresia variantei estimatorului ![]() , rezulta:
, rezulta:
![]() .
.
Relatia gasita se poate scrie si astfel: 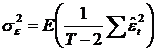 , asa ca, notand
, asa ca, notand ![]() , am obtinut:
, am obtinut: ![]() , adica
, adica ![]() este un estimator
nedeplasat pentru
este un estimator
nedeplasat pentru ![]() (varianta
erorilor).
(varianta
erorilor).
Este de remarcat ca modelul ![]() presupune estimarea a
doi parametri (a si b), iar numitorul lui
presupune estimarea a
doi parametri (a si b), iar numitorul lui ![]() este T- (T-2)
constituie "numarul gradelor de
libertate". Vom reveni ulterior asupra acestei probleme.
este T- (T-2)
constituie "numarul gradelor de
libertate". Vom reveni ulterior asupra acestei probleme.
In concluzie, pentru modelul liniar al regresiei simple, avem estimatorii:
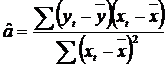
![]()
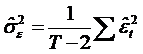
Estimatorul ![]() permite sa
dam o estimatie a variantelor si covariantei
parametrilor din model, deci o estimatie a matricei
permite sa
dam o estimatie a variantelor si covariantei
parametrilor din model, deci o estimatie a matricei ![]() , notata
, notata ![]() :
:
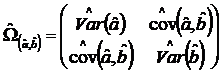 , unde:
, unde:
 ,
,
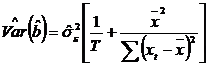 ,
,
![]() .
.
2.3.3. Interpretarea geometrica a metodei celor mai mici patrate
Am determinat estimatorii ![]() si
si ![]() ai parametrilor
modelului utilizand conditia necesara de existenta a
minimului sumei patratelor erorilor
ai parametrilor
modelului utilizand conditia necesara de existenta a
minimului sumei patratelor erorilor ![]() . Putem sa dam o conditie necesara
si suficienta pentru ca
. Putem sa dam o conditie necesara
si suficienta pentru ca ![]() sa fie
minimala, cu ajutorul unei reprezentari grafice. Aceasta
conditie va consta in egalitatea cu zero a doua produse scalare care
redau ecuatiile normale.
sa fie
minimala, cu ajutorul unei reprezentari grafice. Aceasta
conditie va consta in egalitatea cu zero a doua produse scalare care
redau ecuatiile normale.
Modelul ![]() se scrie sub
forma matriceala astfel:
se scrie sub
forma matriceala astfel: ![]() ,
,
unde: 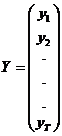 ,
, 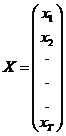 ,
, 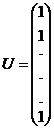 ,
, 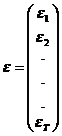 .
.
In spatiul
ortonormat ![]() consideram
vectorii Y, X, U si e
consideram
vectorii Y, X, U si e
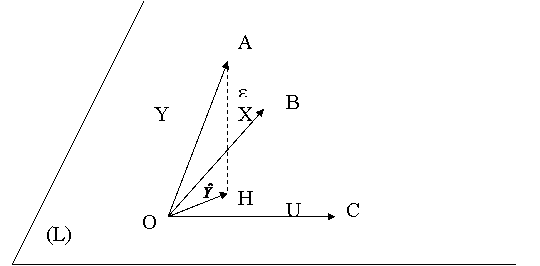

Vectorul 0H=aX+bU
apartine planului (L) determinat de vectorii X si U. Fie 0A=Y, 0B=X, 0C=U, HA=e. Cantitatea ![]() este minimala
daca HA este ortogonal pe (L),
adica pe X si U. Aceasta conditie se traduce
prin egalitatea cu zero a produsului scalar al vectorilor respectivi:
este minimala
daca HA este ortogonal pe (L),
adica pe X si U. Aceasta conditie se traduce
prin egalitatea cu zero a produsului scalar al vectorilor respectivi: ![]() , sau
, sau ![]() , adica
, adica 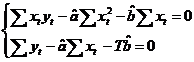 .
.
Am regasit, deci, sistemul de ecuatii normale.
Notam ![]() proiectia pe
planul (L) a vectorului Y si cu
proiectia pe
planul (L) a vectorului Y si cu ![]() vectorul HA ortogonal
la planul (L).
vectorul HA ortogonal
la planul (L).
A efectua o regresie a variabilei Y
asupra variabilei X in modelul ![]() revine, deci, la a
proiecta vectorul Y pe planul (L) din
revine, deci, la a
proiecta vectorul Y pe planul (L) din
![]() determinat de X si U.
determinat de X si U.
Observatie
Consideram
modelul ![]() . O reprezentare analoga celei dinainte este:
. O reprezentare analoga celei dinainte este:


In
scriere matriciala, modelul este ![]() , iar conform cu reprezentarea grafica, avem
relatia OA=OH+HA.
, iar conform cu reprezentarea grafica, avem
relatia OA=OH+HA.
![]() este minimala
daca
este minimala
daca ![]() (HA este perpendicular pe 0H),
adica
(HA este perpendicular pe 0H),
adica ![]() sau
sau ![]() sau
sau ![]() ,
, ![]() si
si ![]() . Masura algebrica a proiectiei vectorului Y pe suportul vectorului U este
. Masura algebrica a proiectiei vectorului Y pe suportul vectorului U este ![]() . Vom utiliza aceasta observatie pentru a exprima
ecuatia variantei.
. Vom utiliza aceasta observatie pentru a exprima
ecuatia variantei.
Ecuatia variantei
Reluam reprezentarea geometrica precedenta si notam cu K proiectia lui A pe suportul vectorului U:
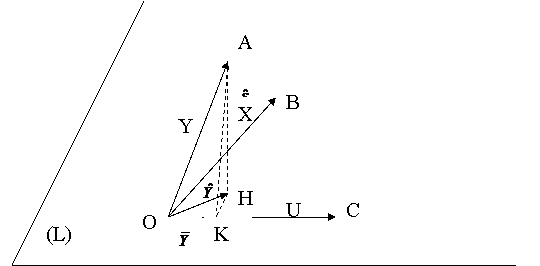

Evident, KH este perpendicular in K pe 0C. In triunghiul AKH, dreptunghic, avem:
![]() .
.
Stim ca ![]() si
si  , adica:
, adica: ![]() . Dar si
. Dar si ![]() , rezultand ca
, rezultand ca ![]() .
.
Deoarece: AK=0A-0K (![]() dreptunghic in K)
dreptunghic in K)
HK=0H-0K (![]() dreptunghic in K),
dreptunghic in K),
rezulta, folosind (1):
![]()
Aceasta este ecuatia variantei. Vom reveni asupra ei cand vom aborda regresia multipla.
3.4. Coeficientul de corelatie liniara
Coeficientul de corelatie liniara intre variabilele X si Y, notat r, se calculeaza cu relatia:
 .
.
In general, ![]() , unde
, unde ![]() si
si ![]() sunt abaterile
standard (radicalul dispersiei) ale variabilelor X si Y.
sunt abaterile
standard (radicalul dispersiei) ale variabilelor X si Y.
Stim ca estimatorul parametrului a are expresia  , astfel ca putem scrie:
, astfel ca putem scrie:
 . Am obtinut o expresie a coeficientului de
corelatie in functie de estimator, iar prin ridicare la patrat:
. Am obtinut o expresie a coeficientului de
corelatie in functie de estimator, iar prin ridicare la patrat: 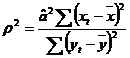 .
.
Un calcul
imediat arata ca: ![]() .
.
In acelasi
timp, ecuatia variantei conduce la: ![]() , de unde:
, de unde: 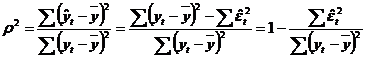 .
.
Pe de alta parte, utilizand figura geometrica si notand
cu α unghiul ![]() , avem
, avem ![]() ,
, 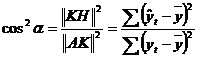 , adica
, adica 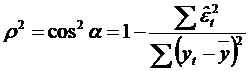 .
.
In mod necesar, ![]() si
si ![]() .
.
Cand ![]() , nu exista o relatie de tip liniar
, nu exista o relatie de tip liniar ![]() intre yt si xt, adica a=0.
intre yt si xt, adica a=0.
Cand ![]() , yt
este legat de xt printr-o
relatie de forma
, yt
este legat de xt printr-o
relatie de forma ![]() .
. ![]() implica a>0
implica a>0
Dupa ce HVB Bank Romania a decis ca va fuziona cu Banca TIRIAC, UniCredito
Italia (reprezentata in Romania prin banca UniCredit, UniCredit Leasing si
UniCredit Securities) a anuntat achizitionarea intregului grup HVB, tranzactie
care a tinut prima pagina a tuturor publicatiilor economice de pe continent
timp de cateva zile.
Va lua astfel nastere o noua entitate bancara europeana, cu peste 28 milioane
de clienti, 7.000 unitati in 19 tari, si active de 733 mld. EUR.
Globalizarea se manifesta nu numai in randul jucatorilor din piata, ci si la nivelul normativelor care trebuie respectate si in privinta modului in care acestia sunt supravegheati de catre organismele de profil. Rolul legislatiei unificate a Uniunii Europene, implementata prin intermediul Directivelor, este de netagaduit.
Ca o concluzie, putem mentiona faptul ca globalizarea este generata de manifestarea a patru importante tendinte: cresterea redusa inregistrata de pietele tarilor puternic industrializate, declinul protectionismului statului, trecerea de la sistemul public de pensii la un sistem privat si lipsa unor perspective reale de supravietuire pentru un anumit tip de asiguratori locali.
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||
|
|||
Proiecte pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








