
| Biologie | Botanica | Chimie | Didactica | Fizica | Geografie |
| Gradinita | Literatura | Matematica |
Matematica
|
|
Qdidactic » didactica & scoala » matematica Trei metode de demonstrare a inegalitatii lui Euler |
Trei metode de demonstrare a inegalitatii lui Euler
Trei metode de demonstrare a
inegalitatii lui Euler ![]() ( * )
( * )
Gizela Pascale
Fie ![]() in care notam cu
a, b, c lungimile laturilor BC, AC, AB si cu R si r raza cercului
circumscris, respectiv inscris triunghiului dat.
in care notam cu
a, b, c lungimile laturilor BC, AC, AB si cu R si r raza cercului
circumscris, respectiv inscris triunghiului dat.
I.
Prima metoda de
lucru consta in a exprima raportul ![]() unde
unde ![]() ,
, ![]() , iar
, iar ![]() cu formula lui Heron.
cu formula lui Heron.
Solutie: ![]() Notam
Notam
2p-2a=x, 2p-2b=y, 2p-2c=z ![]()
![]() . Obtinem
. Obtinem ![]() . Cum
. Cum ![]()
![]()
![]()
![]()
![]() de unde
de unde ![]() ceea ce conduce
la
ceea ce conduce
la ![]() ( * ) cu egalitate
( * ) cu egalitate ![]() x=y=z
x=y=z ![]() a=b=c, adica
a=b=c, adica ![]() echilateral.
echilateral.
II. A doua metoda de lucru
consta in stabilirea relatiei lui Euler: ![]() unde C(I, r), C(O, R) reprezinta cercul inscris,
respectiv circumscris
unde C(I, r), C(O, R) reprezinta cercul inscris,
respectiv circumscris
![]() . Cum
. Cum ![]()
![]() ( * ).
( * ).
Solutie: Fie ![]() C(O, R)
C(O, R)![]() . Din
. Din ![]() ABD cu teorema sinusului obtinem
ABD cu teorema sinusului obtinem  si in
si in ![]() exprimam
exprimam 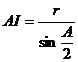 (1), unde P este
proiectia punctului I pe latura AB. Se constata cu usurinta ca
(1), unde P este
proiectia punctului I pe latura AB. Se constata cu usurinta ca 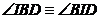 ( fiecare are masura
( fiecare are masura ![]() ), deci
), deci ![]() DBI este isoscel cu ID BD
DBI este isoscel cu ID BD![]()
|
![]() (2). In
(2). In ![]() AOD aplicam teorema lui Stewart si obtinem
AOD aplicam teorema lui Stewart si obtinem ![]()
![]()
![]() . Cum
. Cum ![]() din (1)+ (2)
obtinem relatia cautata, de unde concluzia.
din (1)+ (2)
obtinem relatia cautata, de unde concluzia.
III. Pentru a demonstra inegalitatea ![]() ( * ), stabilim mai intai relatia
lui Carnot:
( * ), stabilim mai intai relatia
lui Carnot: ![]() , unde cu
, unde cu ![]() am notat distantele de la centrul cercului circumscris
triunghiului ABC la laturile de lungimi a, b, c, iar M, N, P sunt
proiectiile punctului O pe laturile BC, AC, AB.
am notat distantele de la centrul cercului circumscris
triunghiului ABC la laturile de lungimi a, b, c, iar M, N, P sunt
proiectiile punctului O pe laturile BC, AC, AB.
Solutie: Patrulaterele APON, BMOP, CNOM sunt inscriptibile si
aplicand teorema lui Ptolemeu in acestea, obtinem de exemplu: ![]() ceea ce conduce la
relatiile
ceea ce conduce la
relatiile ![]() ;
; ![]() ;
; ![]() .
.
Adunand aceste trei egalitati si grupand convenabil ![]()
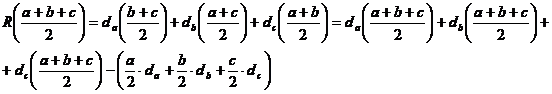
prin urmare  deci
deci
![]() . Am folosit
. Am folosit ![]() , deci obtinem relatia lui Carnot.
, deci obtinem relatia lui Carnot.
Mai departe vom demonstra teorema lui Paul Erdos care afirma ca:
Daca P este un punct care apartine interiorului triunghiului ABC ascutitunghic si A', B', C' sunt proiectiile punctului P pe laturile triunghiului, atunci are loc:
AP+BP+CP![]() 2( P A'+P B'+P C').
2( P A'+P B'+P C').
Solutie: Fie AP=![]() , BP
, BP![]() , CP
, CP![]() , P A'
, P A'![]() , P B'
, P B'![]() , P C'
, P C'![]() Inegalitatea din enunt este echivalenta cu
Inegalitatea din enunt este echivalenta cu ![]()
Patrulaterul A B'P C' este inscriptibil deci B'C'![]() Analog
exprimam A'C' si
Analog
exprimam A'C' si
A'B'. Fie ![]() si
si ![]() proiectiile
punctelor C' si B' pe BC. Atunci
proiectiile
punctelor C' si B' pe BC. Atunci ![]()
![]()
![]() A
A ![]() A'.
Fie
A'.
Fie ![]()
![]() C'; m(
C'; m(![]() DP C')
DP C')![]()
![]() cos(
cos(![]() DP C')
DP C')![]() de unde
de unde ![]()
![]() A si
analog
A si
analog ![]() A
A ![]() , deci
, deci ![]() Cum B'C'
Cum B'C'![]() obtinem
obtinem ![]()
![]() si analoagele:
si analoagele:
![]()
![]() , prin adunarea acestor ultime trei inegalitati
obtinem
, prin adunarea acestor ultime trei inegalitati
obtinem ![]() Cu datele obtinute putem demonstra acum inegalitatea lui
Euler.
Cu datele obtinute putem demonstra acum inegalitatea lui
Euler.
Fie ![]() inlocuind in inegalitatea Paul Erdos, obtinem
inlocuind in inegalitatea Paul Erdos, obtinem ![]() . Cum
. Cum ![]()
![]() , prin urmare
, prin urmare ![]() ( * )
( * )
Bibliografie:
Buletin matematic, Vol.1, Targoviste, 1987.
Nicolescu L., Boskoff V., Probleme practice de geometrie, Editura Tehnica, Bucuresti, 1990.
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||
|
|||
|
|||
Esee pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








