
| Biologie | Botanica | Chimie | Didactica | Fizica | Geografie |
| Gradinita | Literatura | Matematica |
Matematica
|
|
Qdidactic » didactica & scoala » matematica Integrarea functiilor rationale |
Integrarea functiilor rationale
INTEGRAREA FUNCTIILOR RATIONALE
Definitie: O functie f:I→R , I interval,
se numeste rationala daca R(x)= ![]() unde f,g sunt functii polinomiale.
unde f,g sunt functii polinomiale.
Daca grad f ![]() grad g, atunci se efectueaza impartirea lui f
la g
grad g, atunci se efectueaza impartirea lui f
la g ![]() f=gq+r, 0
f=gq+r, 0![]() grad r<grad g si deci
grad r<grad g si deci ![]()
1 ![]() Ex.
Ex. ![]()
2 ![]() Ex
Ex ![]()
3 ![]() Ex
Ex ![]()
4 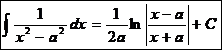 Ex
Ex ![]()
5*
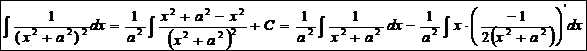
Ex.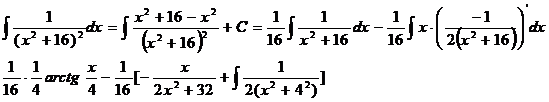
6 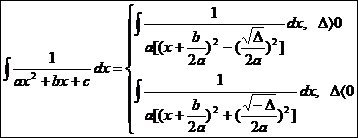
Ex 
Ex ![]()
7.![]() Ex.
Ex.
![]()
|
8*.
![]()
Ex 
Sa se calculeze
1. ![]() 2.
2. ![]() 3.
3. ![]() 4.
4. ![]()
5. ![]() 6.
6. ![]() 7.
7. ![]() 8.
8. ![]()
9. ![]() 10.
10. ![]() 11.
11. ![]() 12.
12. ![]()
13. ![]() 14.
14. ![]() 15.
15. ![]() 16.
16. ![]()
17. ![]() 18.
18. ![]() 19.
19. ![]() 20.
20. ![]()
21. ![]() 22.
22. ![]() 23.
23. ![]() 24.
24. 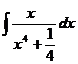 25.
25. ![]() 26.
26. ![]() 27.
27. ![]() 28.
28. ![]()
29. ![]()
Rezolvari.
23.
Notam![]() cu t
cu t![]()
![]()
![]()

26. Notam pe![]() cu t
cu t ![]() 4
4![]() dx=dt
dx=dt ![]()
![]()
27. Notam pe x-1 cu t ![]() x=t+1
x=t+1 ![]() dx=dt
dx=dt ![]()
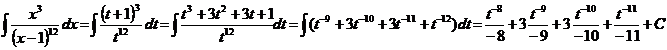
= ![]()
28. Notam pe x-1cu t ![]()
![]()
Sa se calculeze integralele folosind descompunerea in fractii rationale simple.
30. ![]() 31.
31. ![]() 32.
32. ![]() 33.
33. ![]()
34. ![]() 34.
34. ![]() 35.
35. ![]() 36.
36. ![]()
37. ![]() 38.
38. ![]() 39.
39. ![]() 40.
40. ![]()
41. ![]() 42.
42. ![]() 43.
43. ![]() 44.
44. ![]()
45. ![]()
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||
|
|||
|
|||
Proiecte pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








