
| Biologie | Botanica | Chimie | Didactica | Fizica | Geografie |
| Gradinita | Literatura | Matematica |
Matematica
|
|
Qdidactic » didactica & scoala » matematica Subiecte examen metode numerice |
Subiecte examen metode numerice
SUBIECTE EXAMEN METODE NUMERICE
[Curs 1] Elemente de teoria aproximarii
Subiectul 1: Complexitatea si ordinul de complexitate al unei probleme numerice
Prin complexitate timp intelegem timpul necesar executiei programului. Inainte de a evalua timpul necesar executiei programului ar trebui sa avem informatii detaliate despre sistemul de calcul folosit. Pentru a analiza teoretic algoritmul, vom presupune ca se lucreaza pe un calculator 'clasic', in sensul ca o singura instructiune este executata la un moment dat. Astfel, timpul necesar executiei programului depinde de numarul de operatii elementare efectuate de algoritm. Privind din perspectiva calculului paralel, acest mod de analiza a complexitatii timp a unui algoritm va fi, probabil, total inadecvat pentru viitoarele generatii de calculatoare. Dar pentru algoritmii 'clasici' ofera un criteriu general de comparatie, fara a fi necesara implementarea si rularea pe un calculator. De altfel, din motive practice, pe calculator nu putem testa algoritmul pentru cazuri oricat de mari si nu putem obtine informatii asupra comportarii in timp a algoritmilor decat pentru seturi particulare de date de intrare.
Subiectul 2: Definitia unei probleme numerice. Exemple de metode numerice.
Combinatia dintre o problema matematica (PM) de natura constructica si specificatiile de precizie ale rezultatului (SP) se numeste problema numerica.
Exemple de metode numerice :
Evaluarea unei functionale ![]() cum ar fi de exemplu,
calcularea valorii unei functii
cum ar fi de exemplu,
calcularea valorii unei functii ![]() , a derivatelor
, a derivatelor  . (derivare numerica), a integralelor definite
. (derivare numerica), a integralelor definite ![]() (integrare numerica) si a normelor
(integrare numerica) si a normelor ![]() , etc.
, etc.
Rezolvarea ecuatiilor algebrice: determinarea valorilor unor necunoscute aflate in relatii algebrice prin rezolvarea unor sisteme de ecuatii liniare sau neliniare.
Rezolvarea unor ecuatii analitice: determinarea functiilor (sau valorilor de functii) solutii ale unei ecuatii operatoriale, cum ar fi ecuatiile diferentiale ordinare sau cu derivate partiale, ecuatiile integrale, etc
Probleme de optimizare: determinarea unor valor numerice particulare ale unor functii, care optimizeaza (minimizeaza sau maximizeaza) o functie obiectiv cu restrictii sau fara restrictii.
Subiectul 3 : Sursele si clasificarea erorilor(cele trei categorii de erori) Masuri ale erorii
In rezolvarea numerica a unei probleme deosebim - in general - trei feluri de erori:
Erori inerente (initiale) Aceste erori provin din: simplificarea modelului fizic pentru a putea fi descris printr-un model matematic; masuratori initiale; calcule anterioare; datele problemei;
Erori de metoda (de trunchiere) care se datoreaza preciziei insuficiente a metodei folosite. Majoritatea metodelor necesita un numar mare de operatii aritmetice (adesea un numar infinit!) pentru a ajunge la solutia exacta a problemei. Acest fapt necesita trunchieri (renuntarea la o multime - eventual infinita - de operatii) si aproximatii;
Erori de rotunjire (de calcul) care apar in datele de intrare, in calculele pe parcurs si in datele de iesire. Astfel, datele de start nu pot fi numere cu o infinitate de cifre deoarece nu putem opera cu acestea. Se inlatura multe cifre - eventual o infinitate - rotunjind numerele date, prin retinerea unui numar finit de cifre. Pe parcursul calculelor numarul cifrelor creste si se impune de asemenea rotunjirea. Chiar rezultatul final se rotunjeste retinandu - se un numar de cifre corespunzator preciziei dorite.
Eroarea totala = erori inerente + erori de metoda + erori de rotunjire
Masuri ale erorii
Definitie1 Fie X
un spatiu liniar normat, ![]() si
si ![]() Un element
Un element ![]() se numeste aproximanta
a lui x din A (notatie
se numeste aproximanta
a lui x din A (notatie ![]()
Definitie2 Daca ![]() este o aproximanta a lui x diferenta
este o aproximanta a lui x diferenta ![]() se numeste eroare, iar
se numeste eroare, iar ![]() se numeste eroare absoluta.
se numeste eroare absoluta.
Prin urmare, expresia  se numeste eroare relativa
se numeste eroare relativa
Subiectul 4 : Definirea erorii asimptotice
Definitie1:
Spunem ca ![]() converge la
converge la ![]() (cel putin liniar) daca
(cel putin liniar) daca
![]() (4.1)
(4.1)
unde ![]() este un sir pozitiv ce satisface
este un sir pozitiv ce satisface
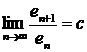
![]() (4.2)
(4.2)
Daca relatiile (4.1) si (4.2) au loc cu egalitate in atunci c se numeste eroare asimptotica. Expresia "cel putin" , se leaga de faptul ca avem doar inegalitate in (4.1), ceea ce dorim in practica.
Subiectul 5: Convergenta procesului iterativ pentru ecuatii neliniare
Evident in cazul unui proces iterativ se doreste convergenta, dar mai mult de atat o convergenta rapida, cand este posibil. Conceptul de baza pentru viteza de convergenta este ordinul de convergenta.
Definitie Spunem ca ![]() converge la
converge la ![]() (cel putin liniar) daca
(cel putin liniar) daca
![]() (3.1)
(3.1)
unde ![]() este un sir pozitiv ce satisface
este un sir pozitiv ce satisface
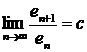 ,
, ![]() .
.
Convergenta de ordinul 1 coincide cu convergenta liniara,
in timp de convergenta p>1 este
mai rapida. In ultimul caz nu avem o restrictie pentru c: odata ce ![]() este sufficient de mic ordinul p va avea grija de convergenta.
este sufficient de mic ordinul p va avea grija de convergenta.
Spunem ca sirul ![]() converge
liniar catre
converge
liniar catre ![]() daca exista o
constanta
daca exista o
constanta ![]() astfel incat
astfel incat
![]() n>p.
n>p.
Sirul ![]() converge patratic
catre
converge patratic
catre ![]() daca exista C si
p astfel incat
daca exista C si
p astfel incat
![]() (3.4)
(3.4)
Sirul ![]() converge
superliniar catre
converge
superliniar catre ![]() daca exista un numar natural p si un alt sir
daca exista un numar natural p si un alt sir ![]() cu
cu ![]() astfel incat
astfel incat
![]() , n>p
, n>p
Subiectul 6 - Metode iterative de rezolvare a ecuatiilor neliniare
6.1 Metoda Newton
Descrierea metodei
Este una din metodele iterative cele mai utilizate in calculul solutiei unei ecuati neliniare.
Fie ecuatia
![]()
![]()
Presupunem ca ecuatia admite o
solutie izolata pe [a,b], ![]() , adica
, adica ![]()
Presupunem urmatoarele conditii pentru f
f continua pe [a,b]
f este derivabila de doua ori pe [a,b] si derivate a-2-a pastreaza semn constant pe [a,b]
derivata I nu se anuleaza pe intervalul specificat
Metodele iterative vor furniza practic
un sir de aproximatii ![]() ce tinde catre
radacina
ce tinde catre
radacina ![]()
|
Ordinul de convergenta va indica numarul de iteratii ce trebuie efectuate pentru a atinge o anumita precizie, data uneori si de eroarea de aproximare. Metodele cu ordin de convergenta mai ridicat tind sa efecueze mai multe operatii pe iteratie.
Continuand
algoritmul, metoda lui Newton construieste astfel un sir de aproximatii
successive ale lui ![]() cu ajutorul
relatiei de recurenta:
cu ajutorul
relatiei de recurenta:
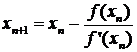
![]()
unde ![]() este abscisa
punctului de intersectie cu axa OX a tangentei la graficul functiei f in punctele de coordonate
este abscisa
punctului de intersectie cu axa OX a tangentei la graficul functiei f in punctele de coordonate ![]()
Se obtine astfel
un sir de aproximatii ![]()
![]() ce in anumite conditii converge la la
ce in anumite conditii converge la la ![]()
O alta problema ar fi stabilirea conditiilor de oprire a procesului iterativ. Una din.
conditii ar fi relatia:
![]()
unde eps reprezinta termenul eroare stabilit la inceputul problemei in anumite situatii..
Cu alte cuvinte procesul iterativ se opreste cand diferenta in modul a doua aproximatii succesive este mai mica decat termenul eroare eps- dat.
6.2 Metoda secantei
Metoda Newton
prezinta inconvenientul de a calcula derivata lui f. Se poate ca
aceasta derivata ![]() sa fie
dificil de calculat. Atunci, se inlocuieste derivata
sa fie
dificil de calculat. Atunci, se inlocuieste derivata ![]() printr-o
aproximatie in functie de valori ale lui f.
printr-o
aproximatie in functie de valori ale lui f.
De exemplu
![]() (3.13)
(3.13)
Metoda
face parte tot din categoria metodelor iterative de rezolvare a unei ecuatii
neliniare. Ipotezele pentru functia f sunt
aceleasi ca si la metoda lui Newton. Numele metodei deriva din interpretarea
geometrica. Mai exact se inlocuieste curba ![]() cu o coarda dusa prin
punctele
cu o coarda dusa prin
punctele ![]() ,
, ![]() .
.
Procedeul iterativ consta in apropierea de
solutia exacta a ecuatiei (2.2.1.) prin punctele de intersectie ale coardelor
duse prin punctele ![]()
![]() si punctul fix
si punctul fix ![]() - punct dat de conditia initiala a problemei iterative.
Aceasta metoda se construieste pe doua conditii initiale, cu alte cuvinte
implica cunoasterea a doua aproximatii ale solutiei exacte l si anume
- punct dat de conditia initiala a problemei iterative.
Aceasta metoda se construieste pe doua conditii initiale, cu alte cuvinte
implica cunoasterea a doua aproximatii ale solutiei exacte l si anume ![]() .
.
Ca si la metoda lui Newton
alegerea lui ![]() se face astfel incat
sa fie verificata relatia
se face astfel incat
sa fie verificata relatia
![]() ,
, ![]() . (3.14)
. (3.14)
Pentru usurinta vom alege unul
din capetele intervalului [a,b] care respecta acesta relatie, iar ![]() va reprezenta celalalt
capat.
va reprezenta celalalt
capat.
Astfel pentru
aflarea aproximantei de ordin 2 vom intersecta secanta determinata de punctele ![]()
![]() - corespunzatoare conditiilor initiale cu ecuatia:
- corespunzatoare conditiilor initiale cu ecuatia:
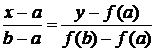
si axa OX, cu ecuatia ![]() .
.
Obtinem

sau
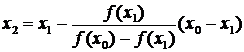 ,
,
in conditiile in care ![]() .
.
Continuand algoritmul pe
aceeasi idee, aproximatia de ordin n+1 se obtine ca intersectie a secantei ![]() cu axa OX
cu axa OX
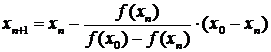
care reprezinta relatia de iteratie pentru metoda secantei.
Subiectul 7 : Algoritmii metodei Newton si secantei
7.1 Metoda lui Newton conduce la urmatorul algoritm :
Intrari f =functia din metoda
fd = derivata functiei f
eps = precizia
nr_max = numarul maxim de iteratii admis
Iesiri x = solutia aproximativa indeplinind eps sau nr_max;
Subiectul 8 : Metoda injumatatirii intervalului[metoda bisectiei]
Fie ecuatia ![]() ,
, ![]() , functie continua.
, functie continua.
Sa presupunem a s-a gasit un
interval ![]() pentru care
pentru care ![]() , cu alte cuvinte exista cel putin o solutie (eventual un
numar impar) in acest interval.
, cu alte cuvinte exista cel putin o solutie (eventual un
numar impar) in acest interval.
Metoda injumatatirii sau
bipartitiei consta in aproximarea
succesiva a radacinii ecuatiei prin mijlocul intervalului [a,b] care se
noteaza cu ![]() .
.
Daca ![]() atunci e este radacina. Daca
atunci e este radacina. Daca ![]() , se calculeaza semnul produsului
, se calculeaza semnul produsului ![]() Daca acesta este
ngativ, atunci radacina se afla in intervalul [a,c], altfel radacina se afla in
[c,b]. Calculele se reiau pe fiecare subinterval.
Daca acesta este
ngativ, atunci radacina se afla in intervalul [a,c], altfel radacina se afla in
[c,b]. Calculele se reiau pe fiecare subinterval.
Metoda este simpla si necesita doar o evaluare de functie pe iteratie. Procesul de impartire a intervalului continua pana cand avem indeplinita una din conditiile de oprire.:
depasirea numarului maxim de iteratii
restrangerea intervalului sub un prag ales eps.
Prin urmare eroarea intre
solutia exacta si aproximanta ![]() este data de"
este data de"
![]() .
.
Metoda bisetiei estre extrem de simpla dar are si cele mai slabe proprietati de convergenta
Algoritmul metodei bisectiei
Intrari : a,b- capetele intervalului
f- functia continua;
eps- precizia;
Iesiri aproximanta solutiei ecuatie data de mijlocul intervalului ![]() ,
,![]() , cu
, cu ![]()
![]()
for k=1:it
![]() ;
;
daca ![]() atunci
atunci ![]()
![]()
altfel daca ![]() atunci
atunci ![]() ;
;
altfel ![]()
![]()
Subiectul 9 - Metode directe de rezolvare a sistemelor liniare. Descrierea metodei lui Gauss
9.1 Aspecte generale
O matrice ![]() , cu
, cu ![]() pentru toti
pentru toti ![]() se numeste inferior triunghiulara.
se numeste inferior triunghiulara.
O matrice ![]() , cu
, cu ![]() pentru toti
pentru toti ![]() se numeste superior triunghiulara
se numeste superior triunghiulara
Algoritmii directi in general daca erorile de rotunjire lipsesc conduc la solutia exacta a sistemului.
Metodele directe aduc sistemul prin transformari de echivalenta, la un sistem particular (diagonal, triunghiular, etc), care se rezolva prin metode elementare.
9.2 Descrierea metodei lui Gauss
Este o metoda in care necunoscutele ![]() se elimina succesiv, sistemul transformandu-se
intr-un sistem echivalent superior triunghiular.
se elimina succesiv, sistemul transformandu-se
intr-un sistem echivalent superior triunghiular.
Astfel, prima necunoscuta calculata
va fi cea de ordin n, ![]() , apoi din penultima ecuatie se calculeaza
, apoi din penultima ecuatie se calculeaza ![]() , functie de
, functie de ![]() , s.a.m.d se calculeaza pe rand toate necunoscutele pe
masura ce inaintam spre prima ecuatie a sistemului.
, s.a.m.d se calculeaza pe rand toate necunoscutele pe
masura ce inaintam spre prima ecuatie a sistemului.
Prin transformari liniare efectuate
asupra elementelor matricei A se aduce primul
element (elementul de pe diagonala principala) la valoarea 1, si celelalte
elemente de sub acesta la valoarea 0, eliminand astfel necunoscuta ![]() din ecuatiile de ordin
din ecuatiile de ordin ![]() .Se ia
apoi a doua coloana si se precedeaza la fel eliminand necunoscutele de ordin
doi,
.Se ia
apoi a doua coloana si se precedeaza la fel eliminand necunoscutele de ordin
doi, ![]() din ecuatiile de ordin
din ecuatiile de ordin ![]()
Algoritmul continua cu eliminarea in acelasi mod a necunoscutelor de ordin 3,4, . n-1
La primul pas, in conditiile in care ![]() , se inmulteste prima ecuatie cu factorul
, se inmulteste prima ecuatie cu factorul ![]()
![]() , si se aduna la ecuatiile de ordin
, si se aduna la ecuatiile de ordin ![]()
Astfel dupa parcurgerea celor (n-1) pasi, sistemul se transforma intr-un sistem triunghiular echivalent.
Subiectul 10 - Metode iterative de rezolvare a sistemelor - Metoda lui Jacobi
Sa consideram sistemul liniar
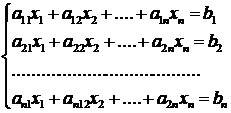
sau matriceal ![]() , astfel incat
, astfel incat ![]() cu
cu


Metoda aduce sistemul la forma a doua, folosind descompunerea matricii sistemului:
![]()
unde D- matricea doagonala corespunzatoare matricii A, ce trebuie sa fie nesingulara, adica ![]() Reamintim ca
matricea diagonala este matricea ce are pe diagonala principala elementele
matricii A, restul sunt 0.
Determinantul unei astfel de matrici este dat de produsul elementelor de pe
diagonala principala.
Reamintim ca
matricea diagonala este matricea ce are pe diagonala principala elementele
matricii A, restul sunt 0.
Determinantul unei astfel de matrici este dat de produsul elementelor de pe
diagonala principala.
Sistemul devine
![]()
De aici rezulta si relatia de iteratie ce genereaza aproximatiile successive ale solutiei exacte a sistemului.
![]()
unde am notat ![]() si
si ![]()
![]()
![]()
Din relatia de iteratie avem:
![]()
![]()
![]()
O conditie de oprire a
procesului iterativ este cand diferenta in modul a doua aproximatii successive
se incadreaza intre limitele erorii ![]()
![]()
Subiectul 11 - Convergenta metodelor iterative de rezolvare a sistemelor de ecuatii liniare(Jacobi si Gauss-Seidel)
11.1 Conditia de convergenta a metodei Jacobi
O conditie suficienta de convergenta a procesului iterativ Jacobi este ca norma matricii de iteratie sa fie subunitara
![]() unde
unde ![]()
Deci conditia necesara si suficienta pentru ca metoda iterativa Jacobi sa convearga este ca matricea sistemului sa fie diagonal dominanta.
11.2 Conditia de convergenta a metodei Gauss-Seidel.
Metoda Gauss-Seidel reprezinta o
modificare a metodei Jacobi in sensul ca la calculul componentei ![]() , se folosesc toate componentele
, se folosesc toate componentele ![]() , deja calculate la iteratia curenta (k+1), impreuna cu
componentele
, deja calculate la iteratia curenta (k+1), impreuna cu
componentele ![]() obtinute la
iteratia precedenta (k).
obtinute la
iteratia precedenta (k).
Convergenta metodei implica dominanta diagonala in cadrul matricii A, unde A este matricea coeficientilor
Pe baza descompunerii se va obtine o relatie de iteratie si cu ajutorul careia vom obtine sirul de aproximatii sucesive pentru solutia exacta a sistemului.
De regula, metoda Seidel - Gauss aduce un plus de viteza de convergenta fata de metoda Jacobi. Astfel, este de asteptat ca, pornind de la o aceeasi aproximatie initiala, metoda Seidel - Gauss sa asigure precizia impusa intr-un numar mai mic de iteratii
Subiectul 12 - Aproximarea functiilor prin polinoame. Aspecte generale
Pentru o functie ![]() problema
aproximarii ei printr-un polinom se pune fie cand este dificil de evaluat f,
fie cand nu se cunoaste expresia analitica a lui f ci doar
valorile ei in anumite puncte
problema
aproximarii ei printr-un polinom se pune fie cand este dificil de evaluat f,
fie cand nu se cunoaste expresia analitica a lui f ci doar
valorile ei in anumite puncte ![]() ,
, ![]() , obtinute in general ca urmare a unor
masurari si prezentate intr-un tabel. Multimea de puncte
, obtinute in general ca urmare a unor
masurari si prezentate intr-un tabel. Multimea de puncte ![]() ,
, ![]() , cu proprietatea
, cu proprietatea ![]() , o vom nota prin
, o vom nota prin ![]() si o vom numi
diviziune a intervalului
si o vom numi
diviziune a intervalului ![]() . Punctele
. Punctele ![]() ,
, ![]() vor fi numite nodurile
diviziunii.
vor fi numite nodurile
diviziunii.
Alegerea unui polinom pentru
aproximarea functiei f se justifica prin modul simplu com Fiind
data o functie arbitrara ![]() se pune problema
stabilirii unui criteriu de alegere a polinomului P care sa
aproximeze functia data. Astfel este necesar un instrument matematic
pentru masurarea distantei dintre doua functii, care impune
situarea intr-un spatiu vectorial normat complet si in functie
de stabilirea criteriului de alegere a polinomului P care sa
aproximeze functia f vom avea metode de aproximare a
functiilor prin polinoame si anume: aproximarea prin interpolare si aproximarea in medie patratica.
se pune problema
stabilirii unui criteriu de alegere a polinomului P care sa
aproximeze functia data. Astfel este necesar un instrument matematic
pentru masurarea distantei dintre doua functii, care impune
situarea intr-un spatiu vectorial normat complet si in functie
de stabilirea criteriului de alegere a polinomului P care sa
aproximeze functia f vom avea metode de aproximare a
functiilor prin polinoame si anume: aproximarea prin interpolare si aproximarea in medie patratica.
Subiectul 13 - Definitia operatorului polinomial
Operatorul de aproximare ![]() cu proprietatea ca
cu proprietatea ca ![]() , se numeste operator
de interpolare, in raport cu multimea
, se numeste operator
de interpolare, in raport cu multimea ![]()
![]()
este formula de interpolare generata de operatorul P iar R este operatorul rest corespunzator.
In general, functionale ![]() sunt valori ale
functiei f sau ale unor derivate ale acesteia in puncte
sunt valori ale
functiei f sau ale unor derivate ale acesteia in puncte ![]() numite noduri de interpolare. Identificand
multimile A si
numite noduri de interpolare. Identificand
multimile A si ![]() vom obtine si
diverse tipuri de operatori de interpolare. Astfel daca A reprezinta
multimea polinoamelor de grad cel mult m,
vom obtine si
diverse tipuri de operatori de interpolare. Astfel daca A reprezinta
multimea polinoamelor de grad cel mult m, ![]() , vom
obtine operatori de interpolare polinomiala.
, vom
obtine operatori de interpolare polinomiala.
Subiectul 14 (Polinomul de interpolare Lagrange)
Fie ![]() si
si ![]()
![]() astfel incat
astfel incat ![]() sa fie toate
distincte. Presupunem ca se cunosc valorile functiei f in
nodurile
sa fie toate
distincte. Presupunem ca se cunosc valorile functiei f in
nodurile ![]()
![]()
![]()
In situatia interpolarii Lagrange,
multimea functionalelor ![]() , reprezinta valorile functiei in nodurile de interpolare
, reprezinta valorile functiei in nodurile de interpolare
![]()
Definitie Problema de interpolare relativ la spatiul ![]() si la
functionalele liniare
si la
functionalele liniare ![]() , definite prin
, definite prin ![]() se numeste problema de interpolare Lagrange.
se numeste problema de interpolare Lagrange.
Aceasta problema consta defapt in determinarea unui polinom P astfel incat
![]() pentru
pentru ![]()
O solutie daca exista, a unei astfel de probleme, se numeste polinom de interpolare Lagrange, notat ![]() , unde n reprezinta gradul polinomului,
asociat functiei f.
, unde n reprezinta gradul polinomului,
asociat functiei f.
Subiectul 15 - Restul in interpolarea Lagrange
Fie ![]() si fie
si fie ![]() . Ce se poate spune despre restul
. Ce se poate spune despre restul ![]() , unde
, unde ![]() este
polinomul de interpolare, astfel ca
este
polinomul de interpolare, astfel ca ![]()
![]()
Se remarca
faptul ca x nu poate sa apartina lui ![]() . In aceste caz, se spune ca avem o extrapolare.
. In aceste caz, se spune ca avem o extrapolare.
Aproximarea
realizata cu ajutorul polinomului de interpolare Lagrange este
nelocala, in sensul ca la evaluarea functiei de interpolat
contribuie informatii din toate punctele de interpolare, nu numai din cele
din vecinatatea argumentului considerat. Aceasta conduce la oscilatii
complet straine de comportarea reala a functiei aproximate. Un
exemplu in acest sens este pentru aproximarea functiei ![]() . Distribuirea in mod echidistant a punctelor de
interpolare reduce oscilatiile pana aproape la disparitie.
. Distribuirea in mod echidistant a punctelor de
interpolare reduce oscilatiile pana aproape la disparitie.
Subiectul 16 - Metoda lui Aitken de calcul iterativ al polinomului Lagrange
Metoda consta in generarea urmatorului tablou:
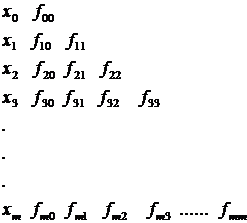
unde ![]() iar
iar
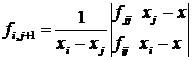
pentru ![]()
Se observa ca

adica ![]() este valoarea
polinomului Lagrange relative la nodurile
este valoarea
polinomului Lagrange relative la nodurile ![]() pe punctual x.
pe punctual x.
In mod asemanator, se poate verifica egalitatea
![]()
![]() fiind polinomul de
interpolare Lagrange relative la nodurile
fiind polinomul de
interpolare Lagrange relative la nodurile ![]()
Prin urmare,
![]()
este un sir de aproximatii ale lui ![]() , constand din valorile polinomului Lagrange respective
de gradul 1,2, . ,m, pe punctual
, constand din valorile polinomului Lagrange respective
de gradul 1,2, . ,m, pe punctual ![]() , nodurile de interpolare fiind luate in ordinea
, nodurile de interpolare fiind luate in ordinea ![]()
Subiectul 17 - Interpolarea cu diferente divizate
Se utilizeaza pentru o baza de date numerice aflata sub forma de a unui tabel
 cu n + 1 de puncte neechidistante , adica la care diferentele dintre
punctele alaturate nu sunt egale
sau la care
cu n + 1 de puncte neechidistante , adica la care diferentele dintre
punctele alaturate nu sunt egale
sau la care
![]()
Diferentele divizate , care sunt elemente caracteristice ale acestei metodei, se definesc dupa formulele:
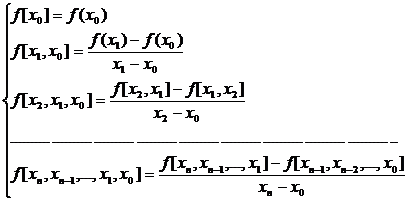
Diferentele divizate au urmatoare proprietati:
ordinea argumentelor este nesemnificativa, de exemplu:
![]()
diferentele divizate se pot fi puse intr-o forma simetrica, de exemplu:

Subiectul 18 - Diferente finite - proprietati ale diferentelor finite
Nodurile de interpolare ![]() sunt echidistante daca
sunt echidistante daca ![]()
![]()
Numim diferenta finita
de ordinul intai in x ![]()
Se verifica direct ca ![]() este un operator liniar, iar diferenta
finita de ordinul k in x se defineste prin relatia
este un operator liniar, iar diferenta
finita de ordinul k in x se defineste prin relatia
![]()
![]() .
.
Formula
de calcul pentru ![]() este urmatoarea:
este urmatoarea:

Subiectul 19 - Polinomul Newton cu diferente finite(ascendent)

Subiectul 20 - Valori si vectori proprii - polinomul caracteristic
Vom arata in cele ce urmeaza cum se ajunge la o problema algebrica de valori si vectori proprii, extinzand problema rezolvarii unui sistem omogen de ecuatii.
Astfel luand sistemul:
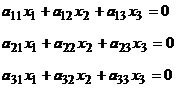
constatam ca acesta se poate scrie sub forma
![]()
unde A
este matricea formata din elementele ![]() cu
cu ![]() si
si ![]() , iar x este vectorul
coloana
, iar x este vectorul
coloana ![]() . Sistemul nu are alte solutii
decat cea banala exceptand cazul
. Sistemul nu are alte solutii
decat cea banala exceptand cazul ![]()
Sa presupunem
ca matricea A depinde de un parametru ![]() si anume sa luam
si anume sa luam
![]()
unde I este matricea unitate.
In acest fel putem cauta acele
valori ![]() pentru care
pentru care ![]() si apoi putem cauta solutiile
nebanale ale ecuatiei
si apoi putem cauta solutiile
nebanale ale ecuatiei ![]()
Problema pe care o avem de rezolvat se poate scrie sun forma:
![]()
Deci o problema algebrica de valori si vectori proprii se exprima prin relatia:
![]()
unde A este o matrice patratica de ordin
n, x un vector (nenul) care se numeste vector propriu (la
dreapta) ce trebuie calculat iar ![]() un numar care se numeste valoare
proprie ce trebuie calculata.
un numar care se numeste valoare
proprie ce trebuie calculata.
Valorile
proprii ![]() pentru problema
pentru problema ![]() sunt radacinile ecuatiei
(numita ecuatie caracteristica):
sunt radacinile ecuatiei
(numita ecuatie caracteristica):
![]()
![]() fiind
un polinom de grad n in
fiind
un polinom de grad n in ![]() obtinut din dezvoltarea determinantului
obtinut din dezvoltarea determinantului ![]() . Avand o
valoare proprie
. Avand o
valoare proprie ![]() , un
vector propriu corespunzator x este solutia nebanala a
sistemului omogen de ecuati.i
, un
vector propriu corespunzator x este solutia nebanala a
sistemului omogen de ecuati.i
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2026 - Toate drepturile rezervate -| |
|
|
|||
|
|||
|
|||
Proiecte pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








