
| Aeronautica | Comunicatii | Drept | Informatica | Nutritie | Sociologie |
| Tehnica mecanica |
Tehnica mecanica
|
|
Qdidactic » stiinta & tehnica » tehnica mecanica Unda de expansiune Prandtl-Meyer |
Unda de expansiune Prandtl-Meyer
Unda de expansiune Prandtl-Meyer
Curgerea supersonica in jurul unui cot deschis sau de-a lungul unui perete plan abrupt, se deosebeste prin aceea ca in zona curburii are loc destindere gazului si accelerarea curentului supersonic.
Zona de destindere reprezinta un evantai atasat la punctul de perturbatie care in dinamica gazelor se numeste unda centrata de expansiune (fig.4.10).

Fig. 4.10. Unda centrata de expansiune:
a - cot deschis; b - perete abrupt; c - portiunea de iesire a ajutajului Laval
Vom examina problema de curgere in jurul unui cot deshis. Problema in cauza a fost rezolvata in premiera de L.Prandtl si R. Meyer.
Se considera curgerea supersonica cu viteza υ1 in jurul unui varf al unui perete cu unghiul deschis AOC (fig.4.11) cunoscut. In varful O se incepe modificarea curgerii.
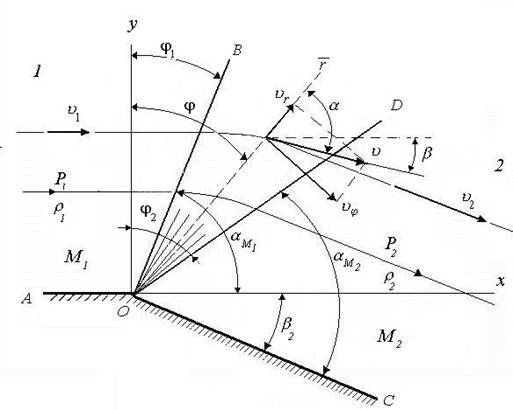
Fig. 4.11. Generarea undei de expansiune la curgerea in jurul unui
perete cu unghiul deschis: b - unghiul de deviere a peretelui.
Sub influenta varfului, care este o perturbatie
slaba, apare o unda slaba, numita unda Mach, care
face cu peretele unghiul ![]() determinat prin
relatia
determinat prin
relatia
![]()
unde a1 este viteza sunetului locala in curentul incident.
Curgerea se face paralel cu peretele inclinat si va
avea viteza υ2 dupa a doua unda
slaba Mach care face unghiul ![]() cu noua directie
a curentului:
cu noua directie
a curentului:
![]()
unde a2 este viteza sunetului locala in avalul undei de expansiune BOD.
Expansiunea are loc in evantaiul BOD, fiind limitata de undele Mach OB si OD. Pe o raza vectoare r se considera un punct in care viteza are marimea υ si este deviata fata de directia initiala la unghiul β. Pe raza aceasta din evantai numita caracteristica parametrii gazodinamici (υ,P,ρ,T) nu se modifica.
Se considera cunoscuti parametrii υ1,P1, ρ1 ai curentului initial si unghiul de deviere a peretelui β2. Se cere determinarea parametrilor υ2,P2, ρ2 dupa unda de expansiune si stabilirea legii de variatie a parametrilor gazodiamici in evantaiul de expansiune limitat de unghiul φ2 - φ1.
Pentru solutionarea problemei se aplica ecuatiile curgerii stationare plane a gazului perfect scrise in coordonate cilindrice x=r cosφ si y=r sinφ (fig.4.9). Din aceste ecuatii fac parte ecuatia de continuitate si ecuatia de vartej:
 , (4.55)
, (4.55)
unde υr este componenta radiala, iar υφ - componenta transversala a vitezei de curgere.
Dar cum in problema examinata curgerea este potentiala, componentele υr, υφ si parametrii P, ρ depind numai de unghiul φ, rezulta:

In continuare la sistemul se adauga ecuatia energiei (ecuatia Bernoulli) scrisa prin vitezele sunetului, avand in vedere ca viteza curgerii in evantaiul de expansiune υ2 = υr2+ υφ2 :
 (4.57)
(4.57)
|
Pentru inchiderea, sistemului se completeaza cu ecuatia procesului adiabatic:

Astfel,avem 4 ecuatii (4.55-4.58) pentru determinarea 4 necunoscutelor P, ρ, υr, υφ .
Relatiile (4.56 a) se transforma astfel :
 ,
,

Dar cum ![]() , unde
, unde ![]() , sau
, sau  ,
,
rezulta
 (4.59)
(4.59)
Separand variabilele, se poate scrie 
Prin integrarea acestei ecuatii, se obtine

sau
 ,
,
unde ![]() este viteza
maxima posibila la curgerea gazului in vid, iar C - constanta
de integrare.
este viteza
maxima posibila la curgerea gazului in vid, iar C - constanta
de integrare.
Asadar ,
 (4.60)
(4.60)
Pentru calculul marimilor υφ, υ si P aplicam consecutiv relatiile (4.56 b),(4.60) si functia π(λ):
 ,
,
 ,
,
 , sau
, sau
 (4.63)
(4.63)
Introducand in examinare unghiul Mach curent a , se pot scrie urmatoare relatii:
![]()
![]()
![]() ,
,
![]()
 ,
,
![]()

Inlocuind in ultima ecuatie υr si υφ din (4.60) si (4.61), rezulta:

de unde
![]() (4.64)
(4.64)
Din geometria curgerii (fig. 4.11) se vede ca unghiul de deviere a vitezei υ fata de directia initiala este:
![]() ,
,
de unde ![]()
Luand in
consideratie ca ![]() , iar
, iar ![]() ,
,
se
obtine ![]() (4.66)
(4.66)
Introducand in ultima ecuatie (4.66) unghiul φ din expresia (4.64) rezulta:
 , (4.67)
, (4.67)
unde ω(M) este functia gazodinamica de expansiune, numita functia Prandl-Meyer.
Constanta C se determina din conditii initiale: M=M1, φ=φ si β=0 .
Rezulta , deci, ![]()
Ecuatia pentru unghiul curent de deviere a vitezei de curgere din evantaiul BOD,care,de fapt, reprezinta unda centrata de expansiune, se scrie sub forma
![]() ,
,
unde ω(M), ω(M1) este functia gazodinamica Prandl-Meyer corespunzatoare numarului Mach M , respectiv M1
Relatia (4.68) fiind dependenta numai de numarul Mach permite, cunoscand unghiul β2, calculul numarului Mach M2 dupa unda de expansiune:
![]()
Frontiera unghiulara a undei de expansiune centrate poate fi determinata din relatia
 (4.70)
(4.70)
Parametrii gazului dupa unda de expansiune se pot gasi usor, reiesind din valorile numarului Mach inainte (M1) si dupa (M2) undei de expansiune, cu ajutorul functiilor gazodinamici p(M), e(M) si t(M), eliminand parametrii gazului franat P0 ,T0 , ρ0
De exemplu, pentru determinarea presiunii P2 dupa unda de expansiune se pleaca de la raporturi:
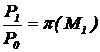 si
si  ,
,
care dau 
La fel se
obtin relatii:  si
si 
Viteza de curgere dupa unda de expansiune se determina din formula
![]()
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||
|
|||
|
|||
Referate pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








