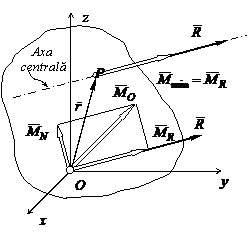| Aeronautica | Comunicatii | Drept | Informatica | Nutritie | Sociologie |
| Tehnica mecanica |
Tehnica mecanica
|
|
Qdidactic » stiinta & tehnica » tehnica mecanica Torsor minimal. Axa centrala. |
Torsor minimal. Axa centrala.
Torsor minimal. Axa centrala.
|
Fig. 3.21 |
Facand reducerea sistemului in diferite
puncte, torsorul va varia prin cea de a doua componenta a sa – momentul ![]() . Daca se face
des-compunerea din fig. 3.21, respectiv:
. Daca se face
des-compunerea din fig. 3.21, respectiv:
![]() (3.47)
(3.47)
se constata ca componenta ![]() este constanta
deoarece proiectia sa
este constanta
deoarece proiectia sa ![]() este un invariant al
sistemului de forte. In consecinta, variatia momentului
rezultant are loc prin componenta sa
este un invariant al
sistemului de forte. In consecinta, variatia momentului
rezultant are loc prin componenta sa ![]() perpendiculara pe
directia rezultantei.
perpendiculara pe
directia rezultantei.
Daca facand reducerea intr-un punct vom gasi
![]() , atunci momentul rezultant va avea o valoare minima,
respectiv
, atunci momentul rezultant va avea o valoare minima,
respectiv ![]() . Torsorul de reducere astfel obtinut poarta numele
de torsor minimal.
. Torsorul de reducere astfel obtinut poarta numele
de torsor minimal.
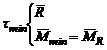 (3.48)
(3.48)
Scalarul momentului minim se calculeaza cu relatia:
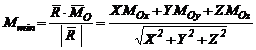 (3.49)
(3.49)
Intr-un punct oarecare P(x,y,z) in care facand reducerea sistemului de forte dat se gaseste un torsor minimal, momentul minim se mai poate exprima, in baza relatiei (3.41) de variatie a torsorului la schimbarea punctului de reducere, prin
![]() (3.50)
(3.50)
in care ![]() . Cu exprimarile analitice corespunzatoare aceasta
relatie ia forma:
. Cu exprimarile analitice corespunzatoare aceasta
relatie ia forma:
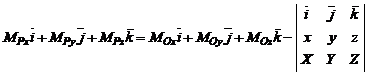 (3.51)
(3.51)
Rezulta proiectiile:
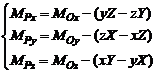 (3.52)
(3.52)
Momentul minim si rezultanta sunt vectori coliniari. Intre proiectiile pe axe exista, conform relatiei (2.25), rapoartele de proportionalitate:
![]() (3.53)
(3.53)
sau, dupa inlocuire,
![]() (3.54)
(3.54)
Aceasta relatie reprezinta ecuatia unei drepte in spatiu avand directia rezultantei. In consecinta , locul geometric al punctelor din spatiu in care facand reducerea unui sistem de forte oarecare se obtine un torsor minimal este o dreapta numita axa centrala a sistemului respectiv.
In mod practic, luand cate doua rapoartele din relatia (3.54) se obtin ecuatiile analitice ale unor plane a caror intersectie este tocmai axa centrala.
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
 |
|||
|
|||
|
|||
Documente online pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||