
| Aeronautica | Comunicatii | Drept | Informatica | Nutritie | Sociologie |
| Tehnica mecanica |
Tehnica mecanica
|
|
Qdidactic » stiinta & tehnica » tehnica mecanica Miscarea si elementele ei - mecanica clasitca |
Miscarea si elementele ei - mecanica clasitca
Miscarea si elementele ei - mecanica clasitca
Pozitia unui corp in spatiu se poate preciza prin intermediul coordonatelor punctului in care se gaseste corpul. Fiecarui punct din spatiul euclidian tridimensional ii corespund trei coordonate. In functie de simetria problemei studiate se pot folosi sisteme de coordonate rectilinii sau curbilinii. Astfel x, y si z sunt coordonate rectilinii (Fig. I.1. a), iar r, q si j sunt coordonate sferice (Fig. I.1.b).


(a) (b)
Fig. I.1.
Se cunosc si alte tipuri de coordonate : polare, cilindrice, etc. Legatura dintre coordonatele carteziene si cele sferice se poate deduce cu ajutorul Fig. I.1. si se concretizeaza in urmatoarele formule :
![]() ,
, ![]() ,
, ![]() . (1)
. (1)
Sa se deduca si relatiile de transformare inverse, respectiv r, q si j in functie de x, y si z.
Pozitia unui corp in spatiu poate fi precizata si cu ajutorul unui vector, numit vector de pozitie, a carui origine se afla in originea sistemului de coordonate si al carui varf se gaseste in punctul in care se gaseste corpul. Intr-un sistem de coordonate carteziene Oxyz vectorul de pozitie are urmatoarea expresie:
![]() , (2)
, (2)
|
x, y si z reprezentand deopotriva coordonatele punctului din spatiu dar si proiectiile vectorului de pozitie pe axele cu acelasi nume. Intre modulul vectorului de pozitie si coordonatele punctului din spatiu in care se afla corpul se stabileste relatia:
![]() . (3)
. (3)
Miscarea corpului presupune schimbarea pozitiei acestuia in raport cu sistemul de coordonate. Succesiunea tuturor pozitiilor din spatiu prin care a trecut corpul in timpul miscarii reprezinta traiectoria urmata de corp, lungimea acesteia fiind o marime scalara.
Daca la momentul t pozitia corpului in spatiu
este descrisa de vectorul de pozitie ![]() , iar la momentul t' t
de vectorul de pozitie
, iar la momentul t' t
de vectorul de pozitie ![]() , diferit de
, diferit de ![]() , atunci se spune ca in intervalul de timp Dt = t'-t s-a produs o deplasare a corpului din pozitia
, atunci se spune ca in intervalul de timp Dt = t'-t s-a produs o deplasare a corpului din pozitia ![]() in pozitia
in pozitia ![]() (Fig. I.2.).
(Fig. I.2.).
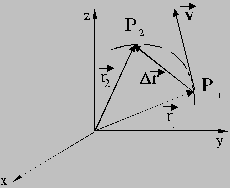
Fig. I. 2
Deplasarea corpului in
intervalul de timp Dt = t'-t
este o marime vectoriala si este definita ca diferenta
dintre vectorii de pozitie ![]() si
si ![]() ai corpului :
ai corpului :
![]() . (4)
. (4)
Sa se identifice situatia in care, desi mobilul parcurge o traiectorie a carei lungime este diferita de zero, totusi deplasarea mobilului este nula.
Pentru a putea preciza cat de repede are loc aceasta deplasare se defineste o alta marime fizica, vectoriala, numita viteza. Viteza instantanee (momentana) a corpului se defineste astfel :
![]() (5)
(5)
si este un vector tangent la traiectorie in orice
punct al acesteia. Unitatea de masura pentru viteza, in Sistemul
International al Unitatilor de Masura (SI), este ![]() . Punctul de deasupra vectorului de pozitie
. Punctul de deasupra vectorului de pozitie ![]() in membrul drept al
relatiei (5) este o alta notatie, mai simpla si foarte des
folosita pentru a marca operatia de derivare a unei marimi
fizice in raport cu timpul. In cazul in care vectorul viteza nu ramane
constant in timp, se defineste acceleratia
momentana a corpului:
in membrul drept al
relatiei (5) este o alta notatie, mai simpla si foarte des
folosita pentru a marca operatia de derivare a unei marimi
fizice in raport cu timpul. In cazul in care vectorul viteza nu ramane
constant in timp, se defineste acceleratia
momentana a corpului:
![]() . (6)
. (6)
Unitatea de masura pentru acceleratie, in
Sistemul International, este ![]()
Miscarea corpurilor poate fi clasificata in functie de anumite particularitati pe care aceasta le prezinta. Astfel, dupa forma traiectoriei, miscarea poate fi rectilinie sau curbilinie. Miscarea poate fi uniforma sau neuniforma, dupa cum viteza corpului variaza sau nu in timpul miscarii. Daca viteza variaza in mod constant, miscarea se numeste uniform variata. Cazul general il reprezinta o miscare in timpul careia atat pozitia cat si viteza si acceleratia corpului se modifica. Legile care descriu aceste modificari se numesc legile miscarii si au urmatoarea forma generala:
![]()
![]() (7)
(7)
![]()
Daca se cunoaste forma explicita a oricareia dintre cele trei legi si conditiile initiale ale miscarii, atunci, cu ajutorul definitiilor (5) si (6), prin derivare si/sau integrare se pot obtine formele explicite ale celorlalte doua legi.
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||
|
|||
|
|||
Referate pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








