Tehnica mecanica
Legi de conservare in mecanica clasica - conservarea energiei, legea de conservare a impulsului, legea de conservare a momentului cinetic
Legi de conservare in mecanica
clasica
Un corp,
sau un sistem de corpuri,
asupra caruia nu actioneaza nici o forta din exterior sau
asupra caruia actioneaza mai multe forte din exterior a caror
rezultanta este insa egala cu zero, se spune ca este izolat. Pentru sistemele izolate se pot
gasi niste functii, scalare sau vectoriale, care depind numai de
coordonatele si de vitezele particulelor constituente si care isi
conserva proprietatile in timpul miscarii. Aceste functii
se numesc integrale prime ale miscarii.
Ele au o proprietate generala importanta : sunt aditive, adica
valoarea lor pentru un sistem format din mai multe particule ale caror
interactiuni reciproce pot fi neglijate, se calculeaza prin insumarea
valorilor acestor functii luate pentru fiecare particula in parte.
Sunt trei astfel de integrale ale miscarii : energia, impulsul si momentul
cinetic.
1. Conservarea
energiei
Legea
conservarii energiei mecanice implica conceptele de energie cinetica, energie potentiala
si lucru mecanic.
Energia cinetica. Se
considera un corp de masa m
asupra caruia actioneaza o forta 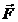 . Asa cum s-a aratat mai sus, in ipoteza fizicii
clasice, principiul fundamental al mecanicii se scrie: . Asa cum s-a aratat mai sus, in ipoteza fizicii
clasice, principiul fundamental al mecanicii se scrie:
 . .
Sub actiunea
fortei 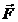 corpul se deplaseaza.
Se noteaza cu corpul se deplaseaza.
Se noteaza cu  deplasarea corpului
efectuata in intervalul de timp deplasarea corpului
efectuata in intervalul de timp  . Acesta se alege atat de mic
incat sa se poata considera ca viteza corpului ramane
practic constanta in acest interval. In acest caz, pentru deplasarea . Acesta se alege atat de mic
incat sa se poata considera ca viteza corpului ramane
practic constanta in acest interval. In acest caz, pentru deplasarea  se poate scrie ca: se poate scrie ca:

Ultimile
doua relatii se inmultesc (scalar membru
cu membru si se obtine:

sau,
tinand cont ca 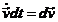
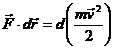 (10) (10)
Cantitatea
din paranteza se noteaza cu 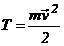 , se numeste energie
cinetica, este o marime scalara, unitatea ei de masura
in SI este 1J (Joule). , se numeste energie
cinetica, este o marime scalara, unitatea ei de masura
in SI este 1J (Joule).
Se
observa ca energia cinetica
a unui corp izolat, pentru care 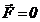 , se conserva, adica ea este o integrala
prima a miscarii acestei particule. Enuntul este adevarat si pentru un
sistem izolat de corpuri. Relatia (10) se mai poate scrie si sub
forma: , se conserva, adica ea este o integrala
prima a miscarii acestei particule. Enuntul este adevarat si pentru un
sistem izolat de corpuri. Relatia (10) se mai poate scrie si sub
forma:
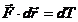 (10') (10')
Lucrul mecanic. Daca
insa  , atunci corpul se va deplasa de-a lungul unei traiectorii
iar relatia (10') se poate integra intre punctele A si B , puncte intre
care are loc deplasarea. Se obtine : , atunci corpul se va deplasa de-a lungul unei traiectorii
iar relatia (10') se poate integra intre punctele A si B , puncte intre
care are loc deplasarea. Se obtine :
 . (11) . (11)
In membrul stang al relatiei
este circulatia vectorului forta intre doua puncte ale unui
anumit contur, in general deschis, iar in membrul drept este diferenta
dintre energiile cinetice ale corpului calculate in aceleasi doua puncte.
Cantitatea din membrul stang este, prin definitie, lucrul mecanic efectuat de forta 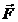 asupra corpului
pentru deplasarea acestuia din punctul A
in punctul B. Relatia (11)
reprezinta astfel teorema de variatie
a energiei cinetice si are urmatorul enunt : asupra corpului
pentru deplasarea acestuia din punctul A
in punctul B. Relatia (11)
reprezinta astfel teorema de variatie
a energiei cinetice si are urmatorul enunt :
Variatia energiei cinetice a unui corp
la deplasarea acestuia intre doua puncte A si B este egala cu
lucrul mecanic efectuat asupra corpului intre aceste puncte de catre forta
aplicata.
Lucrul
mecanic este o marime scalara avand aceeasi unitate de masura
ca si energia cinetica.
In
general, valoarea lucrului mecanic efectuat de o forta pentru
deplasarea unui corp intre doua puncte depinde de drumul pe care se face
deplasarea. Exista insa o categorie de forte, numite forte conservative, pentru care lucrul mecanic efectuat nu depinde de
drumul ales intre cele doua puncte. Altfel spus, pentru fortele
conservative este adevarata relatia:
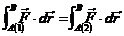 (12) (12)
unde numerele 1 si 2
marcheaza doua trasee diferite intre punctele A si B (vezi Fig.3).
Dupa inversarea limitelor de integrare in
membrul drept si dupa trecerea integralei astfel obtinuta
tot in membrul stang, se obtine:
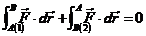 , ,
sau inca:
 . (13)a fac . (13)a fac
Deci lucrul mecanic al fortelor conservative pe un contur inchis este
egal cu zero. Acest enunt este echivalent cu cel de mai sus si
poate servi de asemenea ca definitie pentru fortele conservative. O a
treia definitie se poate gasi folosind teorema lui Stokes-Ampère:
 , ,
sau inca
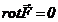 . (14) . (14)
G
|
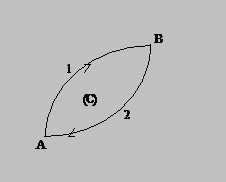
Fig.
Fortele gravitationale,
coulombiene, elastice reprezinta cateva exemple de forte
conservative.
Doua campuri de forte stationare au expresiile analitice 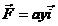 si
si  , unde
, unde 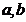 sunt constante nenule,
sunt constante nenule,
 sunt variabile
independente iar
sunt variabile
independente iar 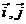 sunt versorii
axelor de coordonate
sunt versorii
axelor de coordonate  . Stabiliti daca cele doua campuri sunt
conservative.
. Stabiliti daca cele doua campuri sunt
conservative.
Energia potentiala.
Se demonstreaza cu usurinta ca este adevarata
urmatoarea relatie :
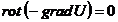 , (15)
, (15)
oricare ar fi functia
scalara de coordonate U(x, y, z),
derivabila si cu derivatele de ordinul intai continue. In aceste
conditii, relatia gasita mai sus pentru fortele
conservative este satisfacuta daca se alege :
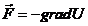 (16)
(16)
Functia
scalara U(x, y, z) astfel
definita se numeste energie
potentiala. Revenind la definitia lucrului mecanic elementar
efectuat de o forta conservativa,

si inlocuind in
aceasta relatie pe 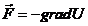 se obtine:
se obtine:

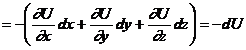 (17)
(17)
Mai departe, pentru a
afla lucrul mecanic total efectuat intre doua puncte A si B din spatiu,
se integreaza relatia de mai sus intre aceste limite:
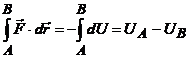 . (18)
. (18)
La
deplasarea corpului din A in B sub actiunea fortei
conservative 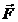 , energia potentiala a corpului se modifica. Relatia
(18) da posibilitatea calcularii doar a variatiei energiei potentiale a corpului la deplasarea
acestuia si nicidecum a energiei potentiale intr-unul din punctele A sau B. Din aceasta cauza se spune ca energia
potentiala se defineste pana la o constanta arbitrara.
, energia potentiala a corpului se modifica. Relatia
(18) da posibilitatea calcularii doar a variatiei energiei potentiale a corpului la deplasarea
acestuia si nicidecum a energiei potentiale intr-unul din punctele A sau B. Din aceasta cauza se spune ca energia
potentiala se defineste pana la o constanta arbitrara.
Daca
insa, prin conventie, se fixeaza valoarea energiei
potentiale intr-un punct oarecare, de exemplu in A, atunci se poate calcula valoarea energiei potentiale intr-un
punct oarecare B de vector de
pozitie  . Astfel, se poate presupune ca
punctul A se gaseste la infinit si ca
. Astfel, se poate presupune ca
punctul A se gaseste la infinit si ca
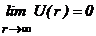 , (19)
, (19)
ceea ce este echivalent
cu a presupune ca energia potentiala a unui corp aflat la o
distanta infinit mare de sursa campului de forte este nula.
In aceasta ipoteza,
pentru energia potentiala a corpului aflat la o distanta  se obtine
expresia :
se obtine
expresia :
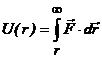 (20)
(20)
Energia potentiala a unui corp aflat
la distanta  intr-un camp de
forte conservative este egala cu lucrul mecanic efectuat pentru a
deplasa acel corp in mod uniform din punctul respectiv de la infinit.
intr-un camp de
forte conservative este egala cu lucrul mecanic efectuat pentru a
deplasa acel corp in mod uniform din punctul respectiv de la infinit.
Trebuie
subliniat ca energia potentiala este o marime fizica
ce se defineste exclusiv in cazul campurilor de forte conservative.
Functia energiei potentiale pentru cei doi atomi ai unei molecule
biatomice poate fi exprimata aproximativ astfel : 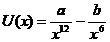 , unde
, unde 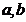 sunt constante
pozitive iar x masoara distanta
dintre atomi. Sa se gaseasca pentru ce valori ale lui x energia potentiala
sunt constante
pozitive iar x masoara distanta
dintre atomi. Sa se gaseasca pentru ce valori ale lui x energia potentiala 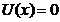 ? Pentru ce valoare a lui x energia potentiala are o valoare minima ? Sa
se reprezinte graficul energiei potentiale si al fortei de
interactiune dintre atomii moleculei.
? Pentru ce valoare a lui x energia potentiala are o valoare minima ? Sa
se reprezinte graficul energiei potentiale si al fortei de
interactiune dintre atomii moleculei.
Asa numitul potential Yukawa 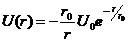 da o descriere destul de precisa a
interactiunii dintre nucleoni. Constanta
da o descriere destul de precisa a
interactiunii dintre nucleoni. Constanta 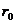 are aproximativ valoarea
are aproximativ valoarea 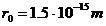 iar constanta
iar constanta  are aproximativ valoarea
are aproximativ valoarea 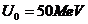 . Sa se afle expresia
corespunzatoare a fortei de atractie dintre nucleoni. Pentru a
arata raza de actiune scurta a acestei forte sa se
calculeze valorile fortelor de atractie pentru cazul in care
nucleonii se afla unul fata de celalalt la distantele
. Sa se afle expresia
corespunzatoare a fortei de atractie dintre nucleoni. Pentru a
arata raza de actiune scurta a acestei forte sa se
calculeze valorile fortelor de atractie pentru cazul in care
nucleonii se afla unul fata de celalalt la distantele  si sa
se raporteze aceste valori la valoarea fortei in cazul in care distanta
dintre nucleoni este
si sa
se raporteze aceste valori la valoarea fortei in cazul in care distanta
dintre nucleoni este 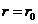
Legea conservarii energiei
mecanice. Se considera un corp de masa m asupra caruia actioneaza
o forta 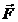 . Sub actiunea acesteia, corpul se deplaseaza
accelerat, in conformitate cu principiul al doilea al mecanicii, intre doua
puncte A si B, pe un anumit drum. S-a
demonstrat in acest caz ca,
. Sub actiunea acesteia, corpul se deplaseaza
accelerat, in conformitate cu principiul al doilea al mecanicii, intre doua
puncte A si B, pe un anumit drum. S-a
demonstrat in acest caz ca,

Daca,
in plus, forta 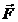 este o forta conservativa,
atunci s-a aratat ca este adevarata si relatia (17):
este o forta conservativa,
atunci s-a aratat ca este adevarata si relatia (17):
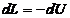
si deci
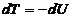
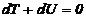
 (21)
(21)
Daca se noteaza
cu E=T+U suma dintre energia cinetica
si cea potentiala si se numeste energie mecanica, atunci se observa ca :
Energia mecanica totala
a unui punct material aflat sub actiunea unor forte
conservative ramane
constanta.
Enuntul este adevarat
si pentru un sistem de puncte materiale care indeplineste aceste
conditii.
Doi protoni avand fiecare energia E=0.5
MeV se indreapta unul catre celalalt. Pana la ce distanta
se pot apropia unul de celalalt cei doi protoni ? Se va considera ca
protonii interactioneaza numai
prin intermediul fortelor electrostatice.
2. Legea de conservare a
impulsului.
Legea de conservare a impulsului deriva direct din
expresia principiului fundamental al dinamicii :
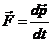 sau inca
sau inca 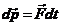 ,
, 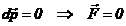 . (22)
. (22)
Daca
asupra unui punct material nu actioneaza nici o forta exterioara
sau actioneaza un sistem de forte a caror rezultanta
este nula, atunci impulsul punctului
material se conserva.
Enuntul ramane
valabil si in cazul unui sistem de mai multe puncte materiale. De
asemenea, trebuie mentionat ca lgea de conservare a impulsului se
aplica si in fizica atomica si nucleara, desi in
acest caz mecanica newtoniana nu mai este valabila.
O particula a
(nucleul unui atom de heliu) este emisa dintr-un nucleu de uraniu 238, initial
in repaus, cu o viteza de  m/s si o energie
cinetica de 4,1 MeV. Sa se afle viteza de recul a nucleului de toriu
234 nou format.
m/s si o energie
cinetica de 4,1 MeV. Sa se afle viteza de recul a nucleului de toriu
234 nou format.
Un
vehicul spatial proiecteaza in urma sa combustibilul ars cu o viteza
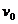 in raport cu
vehiculul ; viteza de variatie a masei vehiculului este egala cu
-a,
si este constanta. Sa se scrie si sa se rezolve ecuatia
de miscare a vehiculului spatial, neglijand gravitatia.
in raport cu
vehiculul ; viteza de variatie a masei vehiculului este egala cu
-a,
si este constanta. Sa se scrie si sa se rezolve ecuatia
de miscare a vehiculului spatial, neglijand gravitatia.
3.
Legea de conservare a momentului cinetic
Sa
consideram un punct material de masa m, care se misca pe o traiectorie curbilinie cu viteza 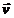 , astfel incat impulsul acestuia este
, astfel incat impulsul acestuia este  . Pozitia punctului material este descrisa cu ajutorul
vectorului de pozitie
. Pozitia punctului material este descrisa cu ajutorul
vectorului de pozitie  , avand originea in originea O a unui sistem de referinta inertial, ca in Figura
4. Se numeste moment cinetic sau moment unghiular marimea fizica
definita astfel :
, avand originea in originea O a unui sistem de referinta inertial, ca in Figura
4. Se numeste moment cinetic sau moment unghiular marimea fizica
definita astfel :
 . (23)
. (23)
Conform definitiei,
modulul, directia si sensul vectorului moment cinetic sunt date de
regula produsului vectorial. Dreapta paralela cu vectorul 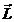 si care trece
prin originea O a sistemului de
referinta se numeste axa
de rotatie.
si care trece
prin originea O a sistemului de
referinta se numeste axa
de rotatie.
Pentru a gasi in ce conditii se conserva
momentul cinetic al unui punct material, se calculeaza mai intai variatia
acestuia :
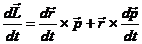 (24)
(24)
Primul termen din membrul
drept este egal cu zero deoarece este produsul vectorial a doi vectori coliniari
iar al doilea termen reprezinta chiar momentul 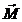 al fortei care actioneaza
asupra punctului material, astfel incat relatia de mai sus devine :
al fortei care actioneaza
asupra punctului material, astfel incat relatia de mai sus devine :
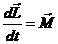 . (25)
. (25)
Se observa din
aceasta relatie ca :
Momentul cinetic al unui
punct material asupra caruia actioneaza o forta
al carei moment este nul,
se conserva.
Enuntul
ramane valabil si in cazul unui sistem de mai multe forte al caror
moment rezultant este nul si de asemenea in cazul unui sistem de puncte
materiale.
Fig. I.4.
Conditia
de mai sus se indeplineste in una din urmatoarele situatii :
a) forta care actioneaza asupra punctului material este egala
cu zero - punctul material este izolat ; b) bratul fortei este
egal cu zero, deci nu se efectueaza o miscare de rotatie in
jurul unei axe ; c) desi nici forta si nici bratul ei
nu sunt egale cu zero, momentul fortei este nul deoarece forta si
bratul ei au aceeasi directie ; aceasta situatie
se realizeaza la randul ei in cazul cand forta are sens invers
vectorului de pozitie, fiind o forta
centrala si in cazul cand are acelasi sens cu vectorul de
pozitie, caz in care iarasi nu se executa o miscare de
rotatie.
Daca miscarea unui punct material se face sub actiunea unei forte
centrale, atunci sa se demonstreaza ca miscarea acestuia
este plana, ca traiectoria miscarii este continuta
intr-un plan.
Acesta
este, de exemplu, cazul miscarii planetelor in jurul Soarelui.
Orbitele planetelor sunt plane eliptice, Soarele aflandu-se intr-unul din focarele
elipsei. Ca urmare a conservarii momentului cinetic rezulta ca
viteza pe orbita creste atunci cand planeta se apropie de Soare si
scade pe masura ce ea se indeparteaza.
Soarele,
planetele si majoritatea satelitilor acestora au, pe langa miscarea
de rotatie pe orbita si o miscare de rotatie in jurul
unei axe proprii. Acestei miscari ii corespunde un moment cinetic
distinct numit momentului cinetic de
spin. In aceste conditii, aplicarea corecta a legii conservarii
momentului cinetic la sistemul solar presupune luarea in consideratie a momentului cinetic total, adica a
sumei dintre momentul cinetic orbital
si momentului cinetic de spin
Exista insa unele corpuri ceresti, de exemplu Luna, care nu au o
miscare de rotatie proprie si ca urmare nu au nici moment
cinetic de spin.
Legile, in
numar de trei, care guverneaza miscarea planetelor in jurul
Soarelui au fost formulate prima data de catre Johannes Kepler
(1571-1630). Acesta a analizat si a interpretat, dupa aproximativ
douzeci de ani de la culegerea lor, datele
obtinute de profesorul sau, Ticho Brahe. Este de remarcat ca
acesta din urma nu a avut la dispozitie nici macar un simplu
telescop, culegandu-si informatiile prin observatie directa.
Legea de conservare a momentului cinetic total functioneaza
si in cazul sistemelor moleculare, atomice sau nucleare. In acest caz insa,
momentul cinetic nu va putea lua decat anumite valori, bine precizate, va fi
deci o marime fizica cuantificata.
 |

|
Tehnica mecanica
|
|
|
Proiecte pe aceeasi tema
|
|
| Ramai informat |
Informatia de care ai nevoie
Acces nelimitat la mii de documente. Online e mai simplu. |
Contribuie si tu!
Adauga online documentul tau.
|
|
|
| |

![]() . Asa cum s-a aratat mai sus, in ipoteza fizicii
clasice, principiul fundamental al mecanicii se scrie:
. Asa cum s-a aratat mai sus, in ipoteza fizicii
clasice, principiul fundamental al mecanicii se scrie: ![]() .
.![]() corpul se deplaseaza.
Se noteaza cu
corpul se deplaseaza.
Se noteaza cu ![]() deplasarea corpului
efectuata in intervalul de timp
deplasarea corpului
efectuata in intervalul de timp ![]() . Acesta se alege atat de mic
incat sa se poata considera ca viteza corpului ramane
practic constanta in acest interval. In acest caz, pentru deplasarea
. Acesta se alege atat de mic
incat sa se poata considera ca viteza corpului ramane
practic constanta in acest interval. In acest caz, pentru deplasarea ![]() se poate scrie ca:
se poate scrie ca: ![]()
![]()
![]()
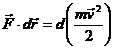 (10)
(10)![]() , se numeste energie
cinetica, este o marime scalara, unitatea ei de masura
in SI este 1J (Joule).
, se numeste energie
cinetica, este o marime scalara, unitatea ei de masura
in SI este 1J (Joule). ![]() , se conserva, adica ea este o integrala
prima a miscarii acestei particule. Enuntul este adevarat si pentru un
sistem izolat de corpuri. Relatia (10) se mai poate scrie si sub
forma:
, se conserva, adica ea este o integrala
prima a miscarii acestei particule. Enuntul este adevarat si pentru un
sistem izolat de corpuri. Relatia (10) se mai poate scrie si sub
forma:![]() (10')
(10')![]() , atunci corpul se va deplasa de-a lungul unei traiectorii
iar relatia (10') se poate integra intre punctele A si B , puncte intre
care are loc deplasarea. Se obtine :
, atunci corpul se va deplasa de-a lungul unei traiectorii
iar relatia (10') se poate integra intre punctele A si B , puncte intre
care are loc deplasarea. Se obtine :![]() . (11)
. (11)
![]() asupra corpului
pentru deplasarea acestuia din punctul A
in punctul B. Relatia (11)
reprezinta astfel teorema de variatie
a energiei cinetice si are urmatorul enunt :
asupra corpului
pentru deplasarea acestuia din punctul A
in punctul B. Relatia (11)
reprezinta astfel teorema de variatie
a energiei cinetice si are urmatorul enunt :![]() (12)
(12)![]() ,
,![]() . (13)a fac
. (13)a fac![]() ,
,![]() . (14)
. (14)










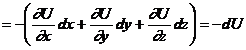
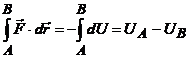 .
.