
| Aeronautica | Comunicatii | Drept | Informatica | Nutritie | Sociologie |
| Tehnica mecanica |
Informatica
|
|
Qdidactic » stiinta & tehnica » informatica Bazele matematice ale graficii 2d |
Bazele matematice ale graficii 2d
Bazele matematice ale graficii 2D
1. Transformari in plan
Daca x si y sunt coordonatele unui punct M, ecuatiile:
x'=f(x,y), y'=g(x,y) (1.14)
permit trecerea de la punctul M(x,y) la punctul. Ecuatiile (1.14.) definesc o transformare punctuala plana. Punctul M este transformatul lui M. Daca ecuatiile de transformare contin si parametri, spunem ca ele reprezinta o familie de transformari.
Putem considera coordonatele punctului ca o matrice 1y2. Fie produsul matricial urmator pe care il notam cu (x',y'):
![]() (1.15)
(1.15)
Atunci toate punctele planului xOy inmultite cu matricea 2x2 vor da noi puncte (x',y'), unde:
x =Ax+Cy, y' =Bx+Dy (1.16)
Transformarea astfel obtinuta va depinde de valorile date variabilelor A, B, C, si D.
Translatia. Transformarea este reprezentata de ecuatiile:
x =x+a, y' =y+b (1.17)
Familia de transformari depinde de parametrii a si b. Daca a=b=0, atunci punctul M(x,y) ramane neschimbat, adica transformarea identica este cuprinsa in familia transformarilor (1.17).
Putem rezolva invers ecuatiile (1.17) si gasim: x = x - a, y = y - b, care sunt ecuatii de aceeasi forma cu (1.17). deci familia contine transformarea inversa.
Presupunem ca efectuam o noua translatie asupra punctului M (x ,y
|
x"=x'+a', y"=y'+b'.
Trecerea de la M(x,y) la M"(x",y") se va exprima prin:
x"=x+(a+a'), y"=y+(b+b'),
adica produsul a doua translatii este tot o translatie.
In
concluzie, translatiile plane formeaza un grup G, cu doi parametri.
Vom observa ca nici-un produs al matricei generale ![]() nu ne permite sa
gasim relatiile (1.17). Pentru rezolvarea situatiei se va
introduce o a treia componenta a vectorilor (x y) si (x' y'),
obtinand (x y 1) si (x' y' 1). Matricea transformarilor
va fi obligatoriu de 3x2:
nu ne permite sa
gasim relatiile (1.17). Pentru rezolvarea situatiei se va
introduce o a treia componenta a vectorilor (x y) si (x' y'),
obtinand (x y 1) si (x' y' 1). Matricea transformarilor
va fi obligatoriu de 3x2:  . Vom arata ca ea furnizeaza bine o
translatie::
. Vom arata ca ea furnizeaza bine o
translatie::

sau : x'=x+a, y'=y+b, unde a produce o translatie pe axa Ox si b pe axa Oy.
Problema translatiei pare a fi rezolvata. Dar o matrice 3x2 nu poseda inversa. De aceea se mai adauga o coloana.
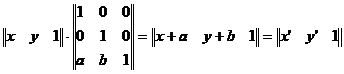
Spunem ca reprezentarea pozitiei unui punct printr-un vector cu trei componente este o reprezentare in coordonate omogene.
La mod general orice punct din plan de coordonate (x, y) are pentru coordonate omogene tripletul (x,y,1) sau nu conteaza care triplet de trei numere proportionale (kx, ky, k), unde k numar real nenul. Deci, x'= kx, y'= ky, z' = k, de unde rezulta: x= x'/k, y= y'/k. Aceste formule reprezinta formulele de trecere de la coordonatele omogene la cele carteziene.
Scalarea. Transformarea este
controlata de matricea T=![]() si in
consecinta (x y). T=(Ax
Dy), adica x'=Ax, y'=Dy.
si in
consecinta (x y). T=(Ax
Dy), adica x'=Ax, y'=Dy.
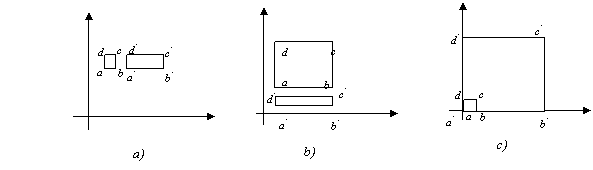
Fig.1.12 Scalarea
Exemplu
1.1 Fie patratul unitar abcd
(fig. 1.12a) si matricea ![]() . Transformans varfurile patratului a(1,2), b(2,2), c(2,3),d(1,3) se
obtin succesiv:
. Transformans varfurile patratului a(1,2), b(2,2), c(2,3),d(1,3) se
obtin succesiv:
(1 2) T=(3 2), a'(3,2);
(2 2) T=(6 2), b'(6,2);
(2 3) T=(6 3), c'(6,3);
(1 3) T=(3 3), d'(3,3)
sau mai simplu:
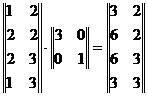
A rezultat astfel un dreptunghi. Produsul matricial a condus la marirea unei laturi pe Ox cu factorul de multiplicare egal cu 3.
Exemplu 1.2 Fie patratul unitar abcd (fig. 1.12b) si matricea
![]() .Aplicand aceasta matrice la coordonatele
patratului se va obtine:
.Aplicand aceasta matrice la coordonatele
patratului se va obtine:
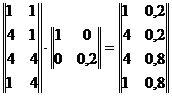
Se observa ca s-a efectuat o modificare cu factorul 0,2 pe axa Oy.
Exemplul 1.3 Daca se doreste marirea / micsorarea uniforma a patratului, pe cele doua axe, trebuie ca valorile coeficientilor A si D sa fie egale (fig.1.12.c)
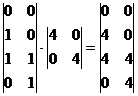
O multiplicare prin matricea T cu A = D = 1 conduce la conservarea patratului.
![]()
adica x = x', y = y'
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
||||||||||||||||||||||||
|
||||||||||||||||||||||||
|
||||||||||||||||||||||||
Lucrari pe aceeasi tema | ||||||||||||||||||||||||
|
| ||||||||||||||||||||||||
|
||||||||||||||||||||||||
|
|
||||||||||||||||||||||||








