
| Aeronautica | Comunicatii | Drept | Informatica | Nutritie | Sociologie |
| Tehnica mecanica |
Comunicatii
|
|
Qdidactic » stiinta & tehnica » comunicatii Sisteme de referinta GPS |
Sisteme de referinta GPS
Sisteme de referinta GPS
1 Introducere
Consideram
ecuatia de baza a observatiilor, care da distanta
topocentrica a satelitului , in functie de vectorul de
pozitie geocentrica a satelitului ![]() si de vectorul de
pozitie geocentrica a statiei
si de vectorul de
pozitie geocentrica a statiei ![]() :
:
![]() (1)
(1)
In ecuatia (1), ambii vectori trebuie exprimati in acelasi sistem de coordonate. Definirea unui sistem cartezian tridimensional necesita o conventie pentru orientarea axelor si pentru pozitia originii.
Pentru aplicatiile specifice geodeziei satelitare, sistemele de coordonate ecuatoriale sunt cele mai potrivite, originea fiind aleasa in centrul de masa al Pamantului (geoentru); doua dintre axele de coordonate (X1, X2) sunt continute in planul ecuatorului terestru, cea de-a treia (X3) fiind dirijata dupa axa polilor.
Conform figurii 1, in functie de orientarea axei X1, pot fi definite doua sisteme rectangulare ecuatoriale:
un sistem
notat ![]() (i=1,2,3), legat de bolta cereasca, la care axa
(i=1,2,3), legat de bolta cereasca, la care axa ![]() este dirijata
catre punctul vernal; acest sistem este inertial si de obicei
este denumit sistem stelar;
este dirijata
catre punctul vernal; acest sistem este inertial si de obicei
este denumit sistem stelar;
un sistem
notat ![]() (i=1,2,3), legat de Pamant, la care axa X1 este dirijata in planul meridianului Greenwich;
acest sistem poate fi considerat fix si este denumit sistem terestru.
(i=1,2,3), legat de Pamant, la care axa X1 este dirijata in planul meridianului Greenwich;
acest sistem poate fi considerat fix si este denumit sistem terestru.
Vectorul de rotatie a Pamantului ![]() joaca rolul axei
joaca rolul axei ![]() in ambele cazuri, iar
axa
in ambele cazuri, iar
axa ![]() este ortogonala
pe axele
este ortogonala
pe axele ![]() si
si ![]() , cu sensul astfel ales incat sa rezulte sisteme de
coordonate orientate dreapta.
, cu sensul astfel ales incat sa rezulte sisteme de
coordonate orientate dreapta.
Un sistem de coordonate a carui origine este amplasata in baricentru este in repaus fata de sistemul solar si astfel conform cu mecanica newtoniana. Trebuie avut in vedere totusi ca, intr-un sistem geocentric, acceleratiile sunt permanent prezente deoarece Pamantul orbiteaza in jurul Soarelui. Intr-un astfel de sistem, legile relativitatii generale trebuie luate in considerare. Intrucat efectul relativistic principal este produs de campul gravitational terestru, sistemul geocentric este convenabil pentru descrierea miscarii unui satelit apropiat de Pamant. Este de remarcat faptul ca axele sistemului de coordonate geocentric raman paralele deoarece miscarea Pamantului in jurul Soarelui este descrisa prin revolutie fara rotatie.
Vectorul
de rotatie a Pamantului, notat cu ![]() , oscileaza datorita mai multor cauze. Ecuatiile diferentiale de
baza ce descriu oscilatiile apartin mecanicii clasice si sunt date de:
, oscileaza datorita mai multor cauze. Ecuatiile diferentiale de
baza ce descriu oscilatiile apartin mecanicii clasice si sunt date de:
![]() (2)
(2)
![]() , (3)
, (3)
unde ![]() este vectorul torsiune
iar
este vectorul torsiune
iar ![]() vectorul de moment
unghiular al Pamantului. Simbolul '
vectorul de moment
unghiular al Pamantului. Simbolul '![]() ' indica un produs vectorial. Torsiunea este
produsa, in primul rand, de fortele gravitationale (de
atractie) ale Soarelui si Lunii, prin urmare este strans legata
de potentialul mareic. Ecuatia (2) da torsiunea intr-un sistem
(cvasi-)inertial, ca de exemplu
' indica un produs vectorial. Torsiunea este
produsa, in primul rand, de fortele gravitationale (de
atractie) ale Soarelui si Lunii, prin urmare este strans legata
de potentialul mareic. Ecuatia (2) da torsiunea intr-un sistem
(cvasi-)inertial, ca de exemplu ![]() , iar (3) da torsiunea in sistemul rotit
, iar (3) da torsiunea in sistemul rotit ![]() . Derivatele partiale exprima variatia
temporala a lui
. Derivatele partiale exprima variatia
temporala a lui ![]() in sistemul terestru
iar produsul vectorial considera rotatia acestui sistem in raport cu
sistemul inertial. Vectorul de rotatie a Pamantului
in sistemul terestru
iar produsul vectorial considera rotatia acestui sistem in raport cu
sistemul inertial. Vectorul de rotatie a Pamantului ![]() este legat de vectorul
de moment unghiular
este legat de vectorul
de moment unghiular ![]() prin tensorul
inertie
prin tensorul
inertie ![]() :
:
![]() . (4)
. (4)
Consideram vectorul ![]() exprimat functie
de versorul sau
exprimat functie
de versorul sau ![]() si norma
si norma ![]() :
:
![]() (5)
(5)
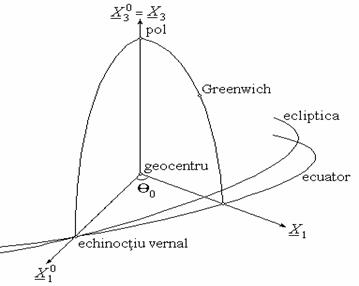
Figura 1. Sistemele de coordonate ecuatoriale
Ecuatiile
diferentiale (2) si (3) pot fi separate in cate doua
parti. Oscilatiile lui ![]() sunt responsabile de
variatiile axei
sunt responsabile de
variatiile axei ![]() si vor fi tratate
la punctul 2.1. Oscilatiile normei determina modificari ale
vitezei de rotatie, care sunt
tratate in capitolul referitor la sistemele de timp.
si vor fi tratate
la punctul 2.1. Oscilatiile normei determina modificari ale
vitezei de rotatie, care sunt
tratate in capitolul referitor la sistemele de timp.
Considerarea
doar a partii omogene (![]() ) a ecuatiilor (2) si (3) conduce la oscilatii
libere. Partea neomogena da oscilatii fortate. In ambele
cazuri, oscilatiile pot fi exprimate in sistemul inertial sau in cel
terestru. O posibilitate de rezolvare in viitor se bazeaza pe utilizarea
tensorului inertiei. Pentru un Pamant rigid si neglijand deplasarea
masei interne, acest tensor este constant, dar nu acelasi lucru se
intampla pentru un Pamant deformabil.
) a ecuatiilor (2) si (3) conduce la oscilatii
libere. Partea neomogena da oscilatii fortate. In ambele
cazuri, oscilatiile pot fi exprimate in sistemul inertial sau in cel
terestru. O posibilitate de rezolvare in viitor se bazeaza pe utilizarea
tensorului inertiei. Pentru un Pamant rigid si neglijand deplasarea
masei interne, acest tensor este constant, dar nu acelasi lucru se
intampla pentru un Pamant deformabil.
2 Sisteme de coordonate
2.1 Definitii
Oscilatiile
axelor. Oscilatia lui ![]() in raport cu
spatiul inertial se numeste nutatie.
Pentru comoditatea calculelor, efectul este partitionat in precesie seculara si nutatie periodica.
Aceeasi oscilatie, in raport cu sistemul terestru, se numeste miscare polara. O
reprezentare simplificata a miscarii polare este data in
figura 2. (sfera polara este considerata de raza 1). Imaginea
pozitiei mijlocii a lui
in raport cu
spatiul inertial se numeste nutatie.
Pentru comoditatea calculelor, efectul este partitionat in precesie seculara si nutatie periodica.
Aceeasi oscilatie, in raport cu sistemul terestru, se numeste miscare polara. O
reprezentare simplificata a miscarii polare este data in
figura 2. (sfera polara este considerata de raza 1). Imaginea
pozitiei mijlocii a lui ![]() este notata cu P.
Oscilatia libera se manifesta ca o miscare a axei de
rotatie de-a lungul unui con circular; pozitia sa mijlocie coincide
cu axa acestui con, care are o deschidere unghiulara de aproape
este notata cu P.
Oscilatia libera se manifesta ca o miscare a axei de
rotatie de-a lungul unui con circular; pozitia sa mijlocie coincide
cu axa acestui con, care are o deschidere unghiulara de aproape ![]() . Pe sfera de raza unitara, aceasta
miscare este reprezentata printr-un cerc cu raza de 6m si
centrul in P. Imaginea unei pozitii instantanee a oscilatiei libere a
axei de rotatie a Pamantului este notata cu R0.
Perioada miscarii libere este de aproximativ 430 zile si este
cunoscuta sub numele de perioada
Chandler. Miscarea fortata se datoreaza
deformatiilor mareice (efectul atractiilor altor corpuri
ceresti) si poate fi de asemenea descrisa printr-un con. Acest
con este reprezentat printr-un cerc avand centrul in R0, raza sa fiind de aproximativ
0,5m. Miscarea fortata are o perioada
. Pe sfera de raza unitara, aceasta
miscare este reprezentata printr-un cerc cu raza de 6m si
centrul in P. Imaginea unei pozitii instantanee a oscilatiei libere a
axei de rotatie a Pamantului este notata cu R0.
Perioada miscarii libere este de aproximativ 430 zile si este
cunoscuta sub numele de perioada
Chandler. Miscarea fortata se datoreaza
deformatiilor mareice (efectul atractiilor altor corpuri
ceresti) si poate fi de asemenea descrisa printr-un con. Acest
con este reprezentat printr-un cerc avand centrul in R0, raza sa fiind de aproximativ
0,5m. Miscarea fortata are o perioada

Figura 2. Miscarea polara a axei de rotatie a Pamantului
apropiata de cea diurna si corespunde partii de forma regulata a potentialului mareic de gradul II (componentele zonale si sectoriale nu au nici o influenta).
Miscarile
axei momentului unghiular, care sunt mai mici de 0',001, sunt foarte
asemanatoare. Miscarea libera a axei momentului unghiular
merita o atentie speciala deoarece miscarea
fortata poate fi corectata prin modelarea atractiei
mareice. Miscarea polara libera are o perioada mare. In
evaluarea ei se pleaca de la o anumita pozitie fixa ![]() , integrarea (2) dand
, integrarea (2) dand ![]() . Acest rezultat implica legea conservarii
momentului unghiular atat timp cat nu este aplicata nici o forta
externa. Datorita proprietatilor mentionate, axa
momentului unghiular este capabila sa serveasca drept axa de
referinta (punctul in care ea 'inteapa' sfera
cereasca este cunoscut in astronomie ca Polul Efemeridelor Ceresti
(CEP). O alta posibilitate de alegere a unei axe de referinta in
sistemul terestru o constituie pozitia mijlocie a axei de rotatie,
notata cu P in figura 2; aceasta pozitie este numita Origine Internationala
Conventionala (CIO). Din
motive istorice, CIO reprezinta pozitia mijlocie a lui
. Acest rezultat implica legea conservarii
momentului unghiular atat timp cat nu este aplicata nici o forta
externa. Datorita proprietatilor mentionate, axa
momentului unghiular este capabila sa serveasca drept axa de
referinta (punctul in care ea 'inteapa' sfera
cereasca este cunoscut in astronomie ca Polul Efemeridelor Ceresti
(CEP). O alta posibilitate de alegere a unei axe de referinta in
sistemul terestru o constituie pozitia mijlocie a axei de rotatie,
notata cu P in figura 2; aceasta pozitie este numita Origine Internationala
Conventionala (CIO). Din
motive istorice, CIO reprezinta pozitia mijlocie a lui ![]() in cursul perioadei
1900 - 1905.
in cursul perioadei
1900 - 1905.
Sistemul
Inertial Conventional. Prin conventie, axa ![]() coincide cu
pozitia axei momentului unghiular la epoca standard J2000,0 (definita
la punctul 3). Axa
coincide cu
pozitia axei momentului unghiular la epoca standard J2000,0 (definita
la punctul 3). Axa ![]() este orientata
spre echinoctiul vernal asociat. In prezent, pozitia acestui
echinoctiu este stabilita cinematic, pe baza unui set de stele
fundamentale. Intrucat acest sistem este definit conventional si
pozitionarea practica nu coincide in mod necesar cu sistemul
teoretic, el se numeste Cadru
Inertial Conventional. Uneori este utilizat termenul
'cvasi-inertial', pentru a evidentia faptul ca
sistemul geocentric nu este riguros inertial datorita
miscarii accelerate a Pamantului in jurul Soarelui.
este orientata
spre echinoctiul vernal asociat. In prezent, pozitia acestui
echinoctiu este stabilita cinematic, pe baza unui set de stele
fundamentale. Intrucat acest sistem este definit conventional si
pozitionarea practica nu coincide in mod necesar cu sistemul
teoretic, el se numeste Cadru
Inertial Conventional. Uneori este utilizat termenul
'cvasi-inertial', pentru a evidentia faptul ca
sistemul geocentric nu este riguros inertial datorita
miscarii accelerate a Pamantului in jurul Soarelui.
Sistemul
Terestru Conventional Prin
conventie, axa ![]() coincide cu
pozitia mijlocie a axei de rotatie, asa cum a fost definita
de CIO. Axa
coincide cu
pozitia mijlocie a axei de rotatie, asa cum a fost definita
de CIO. Axa ![]() este
continuta in planul meridianului Greenwich. Pozitionarea acestui
sistem se realizeaza pe baza unui set de statii de control (ce
servesc drept puncte de referinta), rezultand asa numitul Cadru Terestru Conventional. Cele
mai multe dintre statiile de control sunt echipate cu instrumente laser
pentru determinarea distantelor spre sateliti (SLR) sau cu
interferometre cu baze foarte lungi (VLBI).
este
continuta in planul meridianului Greenwich. Pozitionarea acestui
sistem se realizeaza pe baza unui set de statii de control (ce
servesc drept puncte de referinta), rezultand asa numitul Cadru Terestru Conventional. Cele
mai multe dintre statiile de control sunt echipate cu instrumente laser
pentru determinarea distantelor spre sateliti (SLR) sau cu
interferometre cu baze foarte lungi (VLBI).
Incepand cu anul 1987, GPS utilizeaza drept sistem de referinta WGS-84 (World Geodetic System). Asociat cu WGS-84 este un elipsoid de revolutie geocentric echipotential care este definit prin patru parametri, inscrisi in tabelul 1. Valorile numerice ale altor parametri pot fi determinate pe baza teoriei elipsoidului echipotential (f=1/298.2572221, b=6356752.714m etc.). Valorile parametrilor au fost adoptate dupa elipsoidul asociat Sistemului Geodezic de Referinta 1980 (GRS-80).
Tabelul 1. Parametrii elipsoidului WGS-84
|
Parametrul si valoarea |
Semnificatia |
|
a = 6378137 |
Semiaxa mare a elipsoidului |
|
J2 = 1082630.10-9 |
Coeficientul zonal de ordinul II |
|
P = 7292115.10-11 rad.s-1 |
Viteza unghiulara a Pamantului |
|
= 3986005.108 ms-2 |
Constanta gravitationala a Pamantului |

Figura Coordonate carteziene si elipsoidale
Un vector X poate fi reprezentat in sistemul terestru fie prin coordonatele carteziene X,Y,Z fie prin coordonatele elipsoidale ,h. Relatiile dintre cele doua seturi de coordonate sunt:
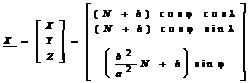 , (6)
, (6)
unde ,h sunt latitudinea, longitudinea si inaltimea elipsoidala, N este raza de curbura a primului vertical, iar a si b sunt semiaxa mare respectiv semiaxa mica a elipsoidului. Detalii suplimentare privind transformarea coordonatelor carteziene si elipsoidale sunt date in capitolul 10.2.1.
2.2 Transformari
Consideratii generale. Transformarea intre Sistemul Inertial Conventional (CIS) si Sistemul Terestru Conventional (CTS) este realizata prin intermediul rotatiilor. Pentru un vector arbitrar x, transformarea este data de
x[CTS] = RM RS RN RP x[CIS] (7) in care:
RM matricea de rotatie pentru miscarea polara;
RS matricea de rotatie pentru timpul sideral;
RN matricea de rotatie pentru nutatie;
RP matricea de rotatie pentru precesie.
Sistemul Inertial Conventional, definit la
epoca standard J2000.0, este transformat intr-un sistem instantaneu
(adevarat) la epoca observatiei, aplicand corectiile datorate
precesiei si nutatiei. Axa ![]() a sistemului
adevarat reprezinta pozitia libera a axei momentului
unghiular si este indreptata catre CEP (Polul Efemeridelor
Ceresti). Rotind acest sistem in jurul axei
a sistemului
adevarat reprezinta pozitia libera a axei momentului
unghiular si este indreptata catre CEP (Polul Efemeridelor
Ceresti). Rotind acest sistem in jurul axei ![]() cu timpul sideral prin
matricea RS,
aceasta axa ramane orientata spre CEP. In final, axa
cu timpul sideral prin
matricea RS,
aceasta axa ramane orientata spre CEP. In final, axa ![]() este adusa
catre polul mijlociu cu matricea RM,
completand transformarea.
este adusa
catre polul mijlociu cu matricea RM,
completand transformarea.
Matricele de rotatie din (7) sunt compuse din matricele elementare Ri si descriu rotatii pozitive ale sistemului de coordonate in jurul axelor Xi, cu unghiul . Expresiile matricelor de rotatie sunt:

![]() (8)
(8)
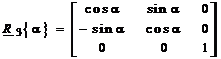
Matricele date in (8) sunt valabile intr-un sistem de coordonate orientat dreapta. Unghiul este pozitiv pentru o rotatie in sensul acelor de ceasornic, privind din origine spre sensul pozitiv al fiecarei axe Xi.
Precesia. O reprezentare grafica a precesiei este data in figura 4. Pozitia echinoctiului vernal mijlociu la epoca standard t0 este notata cu E0 iar pozitia la epoca observatiei este notata cu E.
Matricea de precesie RP contine trei rotatii succesive:
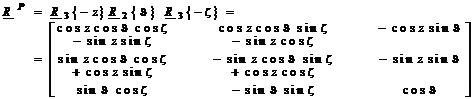 . (9)
. (9)
Figura 4. Precesia
In
relatia (9) z,![]() ,
,![]() sunt parametrii precesiei, exprimati ca serii de timp.
Conform Nautical Almanac Office (1983),
valorile lor sunt date de expresiile:
sunt parametrii precesiei, exprimati ca serii de timp.
Conform Nautical Almanac Office (1983),
valorile lor sunt date de expresiile:
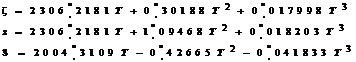 (10)
(10)
Parametrul T reprezinta diferenta de timp, exprimata in secole Iuliene de 36525 zile solare mijlocii, intre epoca standard J2000.0 si epoca observatiei.
Exemplu numeric.
Consideram ca epoca observatiei este J1990,5, care corespunde la
T= -0,095. Cu relatiile (10),
sunt obtinute valorile numerice ![]() ,
, ![]() si
si ![]() . Inlocuind aceste valori in (9), rezulta
urmatoarea matrice numerica de precesie:
. Inlocuind aceste valori in (9), rezulta
urmatoarea matrice numerica de precesie:
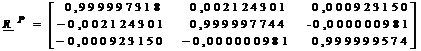 .
.
Nutatia O reprezentare grafica a nutatiei este data in figura 5. Echinoctiul vernal mijlociu la epoca observatiei este notat cu E, iar echinoctiul adevarat este notat cu Et.
Matricea de nutatie RN este obtinuta prin trei rotatii succesive. Nutatia in longitudine si nutatia in oblicitate sunt tratate drept cantitati diferentiale:
 . (11)
. (11)
Conform Nautical Almanac Office (1983), oblicitatea medie a eclipticii este data de expresia
= 23 26 21'.448 - 46'.8150 T - 0'.00059 T 2 + 0'.001813 T 3 (12)
unde T este acelasi factor de timp ca in (10). Parametrii nutatiei si sunt calculati prin serii armonice:
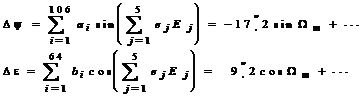 (13)
(13)
Amplitudinile ai,bi precum si coeficientii intregi ej sunt tabelati ca de exemplu in Nautical Almanach Office (1983). Cele cinci argumente fundamentale Ej descriu miscarile medii in sistemul Soare-Pamant-Luna. Longitudinea medie m a nodului ascendent al Lunii este unul dintre argumente, cu o contributie importanta in termenii principali ai seriilor nutatiei. Nodul Lunii are o miscare retrogada, cu o perioada de aproape 18,6 ani.
Timpul sideral. Matricea de rotatie RS pentru timpul sideral este
![]() . (14)
. (14)
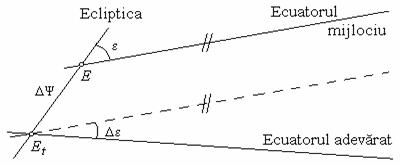
Figura 5. Nutatia
Calculul timpului sideral aparent Greenwich 0 este prezentat in capitolul
Sistemul WGS-84 are intre parametrii de definitie viteza unghiulara uniforma P (vezi tabelul 1). Prin urmare, in cazul GPS, pentru unghiul de rotatie din (14) trebuie folosit in loc de timpul sideral, timpul sideral mediu.
Miscarea
polului Aplicarea
rotatiilor tratate pana aici asigura orientarea axei ![]() catre Polul Efemeridelor Ceresti (CEP).
Mai trebuie executata numai rotirea acesteia pentru a trece in Originea Internationala
Conventionala (CIO). Acest lucru este realizat cu ajutorul
coordonatelor xP,yP ale polului instantaneu,
definite asa cum se prezinta in figura 6. Aceste coordonate sunt
determinate de Serviciul
International de Rotatie a Pamantului (IERS) si sunt
disponibile la cerere. Matricea de rotatie pentru miscarea
polara RM este
catre Polul Efemeridelor Ceresti (CEP).
Mai trebuie executata numai rotirea acesteia pentru a trece in Originea Internationala
Conventionala (CIO). Acest lucru este realizat cu ajutorul
coordonatelor xP,yP ale polului instantaneu,
definite asa cum se prezinta in figura 6. Aceste coordonate sunt
determinate de Serviciul
International de Rotatie a Pamantului (IERS) si sunt
disponibile la cerere. Matricea de rotatie pentru miscarea
polara RM este
 . (15)
. (15)
Matricile de rotatie ![]() si
si ![]() pot fi combinate
astfel incat sa formeze o singura matrice
pot fi combinate
astfel incat sa formeze o singura matrice ![]() care defineste
rotatia Pamantului:
care defineste
rotatia Pamantului:
![]() . (16)
. (16)
In cazul
GPS, sistemul spatial de coordonate este deja legat de CEP. De aici rezulta
ca ![]() este singura matrice
de rotatie care trebuie aplicata pentru transformare in sistemul
terestru.
este singura matrice
de rotatie care trebuie aplicata pentru transformare in sistemul
terestru.

Figura 6. Coordonatele polului
3 Sisteme de timp
1 Definitii
In tabelul 2 sunt enumerate principalele sisteme de timp care sunt de folosinta curenta. In prima coloana a acestui tabel apare procesul periodic in raport cu care sunt definite sistemele respective.
Timpul solar si timpul sideral. O posibilitate de masurare a rotatiei Pamantului o ofera unghiul orar, care este unghiul dintre meridianul unui corp ceresc si un meridian de referinta (preferabil meridianul Greenwich). Timpul universal este definit de unghiul orar Greenwich masurat in raport cu un Soare fictiv (care se misca in planul ecuatorial, cu viteza uniforma); din ratiuni practice, acest unghi este marit cu 12 ore. Timpul sideral este definit ca unghiul orar al echinoctiului vernal. Luand echinoctiul mijlociu ca referinta, rezulta timpul sideral mijlociu iar in raport cu echinoctiul adevarat rezulta timpul sideral adevarat sau aparent.
Timpul solar si timpul sideral nu au o scara uniforma deoarece viteza unghiulara P nu este constanta. Fluctuatiile sunt datorate, in primul rand, variatiilor momentului polar al inertiei din cauza deformatiilor mareice si altor transporturi de masa. O alta cauza o constituie oscilatiile axei de rotatie a Pamantului in jurul unei pozitii medii. Timpul universal corectat pentru miscarea polara este notat cu UT1.
Tabelul 2. Sisteme de timp
|
Procesul periodic |
Sistemul de timp |
|
Rotatia Pamantului |
Timpul Universal (UT) Timpul Sideral Greeenwich (0) |
|
Revolutia Pamantului |
Timpul Dinamic Terestru (TDT) Timpul Dinamic Baricentric) (BDT) |
|
Oscilatii atomice |
Timpul Atomic International (IAT) Timpul Universal Coordonat (UTC) Timpul GPS (GPST) |
Timpul dinamic. Un sistem de timp derivat din miscarea planetara in sistemul solar se numeste timp dinamic. Timpul Dinamic Baricentric (BDT) este un sistem de timp inertial in sens Newtonian; este un argument independent al ecuatiilor de miscare in raport cu baricentrul sistemului solar. Timpul Dinamic Terestru cvasi-inertial (TDT) a fost numit timpul efemeridelor si serveste la integrarea ecuatiilor diferentiale ce descriu miscarea satelitilor in jurul Pamantului; unitatea sa este o zi de 86400 secunde SI la nivelul mediu al marii.
Timpul atomic. O realizare practica a sistemului de timp dinamic este obtinuta prin utilizarea scarii de timp atomic, scara deosebit de uniforma dar independenta de miscarea reala a Pamantului. Timpul GPS apartine acestui sistem. Timpul Universal Coordonat (UTC) reprezinta un compromis; unitatea sistemului este secunda atomica, dar pentru a pastra sistemul aproape de UT si pentru a aproxima timpul civil, se fac salturi de secunde intregi, la anumite epoci. Sistemul GPS are un deplasament constant de 19 secunde fata de Timpul Atomic International (IAT) si a coincis cu UTC la epoca GPS standard 1980, Ianuarie 6Z,0.
2 Conversii de timp
Conversia intre timpii derivati din rotatia Pamantului (de exemplu intre timpul solar mijlociu corectat pentru miscarea polului UT1 si timpul sideral aparent 0) se face cu relatia:
0 = 1.002737909UT1 + ![]() 0 + Dy cos (17)
0 + Dy cos (17)
Primul termen din (17) corecteaza diferenta de
scara dintre timpul solar si timpul sideral iar marimea ![]() 0 reprezinta timpul sideral actual la miezul
noptii Greenwich (0h UT). Al treilea termen constituie
proiectia lui Dy pe ecuator si
corecteaza efectul nutatiei. Timpul sideral mijlociu este
obtinut din (17) prin neglijarea termenului nutatiei si
constituie o parte a mesajului de navigatie transmis de satelitii
GPS.
0 reprezinta timpul sideral actual la miezul
noptii Greenwich (0h UT). Al treilea termen constituie
proiectia lui Dy pe ecuator si
corecteaza efectul nutatiei. Timpul sideral mijlociu este
obtinut din (17) prin neglijarea termenului nutatiei si
constituie o parte a mesajului de navigatie transmis de satelitii
GPS.
Pentru
estimarea lui ![]() 0, Nautical
Almanach Office (1983), recomanda urmatoarea serie de timp:
0, Nautical
Almanach Office (1983), recomanda urmatoarea serie de timp:
![]() 0 = 24110S,54841
+ 8640184S,812866 T + +
0S,093104 T
2 - 0S,0000062 T 3 (18)
0 = 24110S,54841
+ 8640184S,812866 T + +
0S,093104 T
2 - 0S,0000062 T 3 (18)
unde T este acelasi ca in relatia (10).
UT1 difera de UTC prin cantitatea dUT1, care este furnizata de Serviciul International pentru Rotatia Pamantului (IERS):
UT1 = UTC + dUT1 . (19)
Cand valoarea absoluta a dimensiunii dUT1 devine mai mare de 0S,9, in sistemul UTC se insereaza o secunda.
In locul timpului dinamic, pentru GPS a fost preferat sistemul de timp atomic. Sunt definite urmatoarele relatii:
IAT = GPS + 19S,000 ofset constant
IAT = TDT - 32S,184 ofset constant (20)
IAT = UTC + 1S,000 n ofset variabil
Actualul numar intreg n este raportat de IERS. De exemplu, in luna ianuarie 1996, valoarea intreaga a fost n=30, deci timpul GPS diferea exact cu 30 secunde de UTC.
3 Calendarul
Definitii Data Iuliana (JD) defineste numarul de zile solare mijlocii scurse incepand cu epoca 1,5 zile, Ianuarie, 4713 B.C. (inainte de Hristos).
Data Iuliana modificata (MJD) este obtinuta scazand 2.400.000,5 zile din data Iuliana. Aceasta conversie reduce numarul de cifre si MJD incepe la mijlocul noptii civile, in loc de amiaza.
Tabelul 3 contine data Iuliana pentru doua epoci standard. Acest tabel permite, de exemplu, calcularea parametrului T al epocii GPS standard. Scazand respectivele date Iuliene si impartind cu 36525 (numarul de zile dintr-un secol Iulian) rezulta T = - 0,1998767967.
Tabelul Epoci standard
|
Data civila |
Data Iuliana |
Semnificatia |
|
1980 ianuarie 6Z,0 |
2444244,5 |
Epoca GPS standard |
|
2000 ianuarie 1Z,5 |
2451545,0 |
Epoca standard curenta (J2000,0) |
Conversia datei. Relatiile preyentate mai jos pentru conversia datei sunt valabile pentru epoci cuprinse intre martie 1900 si februarie 2100.
Fie data civila exprimata de valori intregi ale anului A, lunii L si zilei Z si o valoare reala a timpului in ore UT. Atunci
JD = INT[365,25.a] + INT[30,6001.(l+1)] + Z + UT / 24 + 1720981,5 (21)
este o conversie in data Iuliana. INT semnifica partea intreaga a numarului real, iar a si l sunt date de:
a = A-1 si l = L+12 daca L 2
a = A si l = L daca L > 2 .
Transformarea inversa, adica transformarea datei Iuliene in data civila, se executa dupa urmatorul algoritm:
1) Se calculeaza numerele auxiliare:
b = INT [ JD + 0,5 ]
c = b + 1537
d = INT [ ( c-122,1) / 365,25 ]
e = INT [ 365,25 d ]
f = INT [ (c - e) / 30,6001 ] .
2) Se calculeaza parametrii datei civile, cu relatiile:
Z = c - e - INT[30,6001.f] + FRAC[JD + 0,5]
L = f - 1 - 12.INT[f / 14] (22)
A = d - 4715 - INT[(7 + L) / 10] , unde FRAC inseamna partea fractionara a numarului.
3) Ca un produs necesar al conversiei datei, ziua din saptamana poate fi evaluata cu relatia
N = modulo , unde N = 0 inseamna luni, N = 1 inseamna marti s.a.m.d. (23)
4) Calculul saptamanii GPS, care este data de relatia:
SAPTAMANA = INT[(JD-2444244,5) / 7] (24)
Formulele date aici pot fi folosite, de exemplu, pentru a obtine date in tabelul 3 sau pentru a verifica faptul ca epoca J2000,0 corespunde zilei de sambata, in a 1042a saptamana GPS.
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2026 - Toate drepturile rezervate -| |
|
|
||||||||||
|
||||||||||
Lucrari pe aceeasi tema
| ||||||||||
|
| ||||||||||
|
||||||||||
|
|
||||||||||









