
| Aeronautica | Comunicatii | Drept | Informatica | Nutritie | Sociologie |
| Tehnica mecanica |
Aeronautica
|
|
Qdidactic » stiinta & tehnica » aeronautica Metoda volumelor finite in rezolvarea problemelor de dinamica fluidelor si de transfer termic |
Metoda volumelor finite in rezolvarea problemelor de dinamica fluidelor si de transfer termic
METODA VOLUMELOR FINITE IN REZOLVAREA PROBLEMELOR DE DINAMICA FLUIDELOR SI DE TRANSFER TERMIC
Sunt analizate principalele modele matematice utilizate in dinamica fluidelor si, in particular, in metodele numerice ale dinamicii fluidelor. Aceste modele corespund diferitelor niveluri de aproximatie ale ecuatiilor fundamentale ale dinamicii fluidelor.
1.1 Formularea conservativa locala
Setul de ecuatii diferentiale care reprezinta modelul matematic al miscarii fluidului este format din [20,21,40,47,68]:
- ecuatia de continuitate :
![]() ; (1)
; (1)
- ecuatiile de impuls :
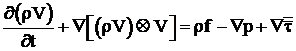 , (2)
, (2)
unde tensorul tensiunilor vascoase ![]() este exprimat
functie de tensorul vitezelor de deformatie
este exprimat
functie de tensorul vitezelor de deformatie ![]() :
:
![]() ; (3)
; (3)
- ecuatia energiei:
 . (4)
. (4)
Ecuatiile de mai sus pot fi scrise sub forma vectoriala:
 , (5)
, (5)
sau inca:
![]() , (6)
, (6)
unde U este vectorul variabilelor conservative, F este vectorul flux iar Q vectorul sursa, marimi definite prin:
 ,
,  ,
,  (7)
(7)
Formularea locala conservativa, in sistem cartezian, se obtine prin particularizarea ecuatiei (6):
 , (8)
, (8)
unde vectorul variabilelor conservative este:
![]() (9)
(9)
1.2 Formularea integrala conservativa
Formularea integrala conservativa se poate obtine prin integrarea ecuatiei vectoriale (6) pe un domeniu arbitrar , urmata de aplicarea teoremei divergentei pentru integrarea fluxului [20,21,40,47,68]:
 , (22)
, (22)
unde ![]() reprezinta
frontiera domeniului
reprezinta
frontiera domeniului ![]() , iar n reprezinta normala la aceasta frontiera.
Reprezentarea (22) deriva direct din aplicarea legilor de conservare,
fiind cea mai 'naturala' formulare a sistemului Navier-Stokes
, iar n reprezinta normala la aceasta frontiera.
Reprezentarea (22) deriva direct din aplicarea legilor de conservare,
fiind cea mai 'naturala' formulare a sistemului Navier-Stokes
3 Scheme cu volume finite. Formulari generale
Daca
vom diviza domeniul W intr-o serie de
subdomenii ![]() , vom putea aplica relatia (22) pe fiecare subdomeniu
, vom putea aplica relatia (22) pe fiecare subdomeniu ![]() marginit de
frontiera
marginit de
frontiera ![]() :
:
 (58)
(58)
unde:
 ,
,  (59)
(59)
Problema
principala in utilizarea schemei (58) este cea referitoare la
discretizarea fluxului F pe frontiera ![]() . Ne vom referi in continuare la divizarea schitata
in fig. 1.
. Ne vom referi in continuare la divizarea schitata
in fig. 1.
1.
In ecuatia (58) scrisa pentru ![]() , apare termenul
, apare termenul  . Desi forma analitica a functiei F(U) este
cunoscuta, trebuie sa specificam functia U pe
interfata dintre doua celule de integrare.
. Desi forma analitica a functiei F(U) este
cunoscuta, trebuie sa specificam functia U pe
interfata dintre doua celule de integrare.
Fluxul exact F, din
ecuatia (58) se inlocuieste cu un flux numeric, aproximativ, ![]() , care depinde de valorile
, care depinde de valorile ![]() din celulele adiacente
frontierei. Spre exemplu, pe frontiera
din celulele adiacente
frontierei. Spre exemplu, pe frontiera ![]() :
:
![]() (60)
(60)
|
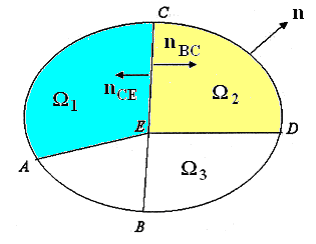
Fig. 1. Divizarea domeniului ![]()
Desi
se poate pune problema extinderii dependentei fluxului numeric ![]() si de valorile
medii
si de valorile
medii ![]() din alte celule, la
ora actuala, practic toate schemele numerice, din motive de eficienta
a calculului considera dependenta localizata la celulele vecine.
din alte celule, la
ora actuala, practic toate schemele numerice, din motive de eficienta
a calculului considera dependenta localizata la celulele vecine.
In consecinta, schema numerica cu volume finite are forma generica:
 (61)
(61)
in care ![]() ,
, ![]() , reprezinta valorile
, reprezinta valorile ![]() de o parte si de
alta a frontierei
de o parte si de
alta a frontierei ![]() .
.
3.1. Definirea grilei si a volumelor de control
Metodele cu volume finite pot fi aplicate fie in grile de tip "diferente finite" (structurate), fie in grile de tip "elemente finite" (nestructurate). Pentru acest caz din urma se impun insa o serie de limitari suplimentare [20,21,40,47,68].
Odata selectata reteaua, sunt doua
variante de a defini volumele finite ![]() (fig. 2): centrat
pe celula si centrat
pe nod.
(fig. 2): centrat
pe celula si centrat
pe nod.

Fig. 2 Tipuri de volume finite
In primul caz, volumele finite sunt reprezentate de celulele grilei de
calcul, iar in a doua situatie se construieste o grila de
integrare formata de volumele ![]() in jurul nodurilor
grilei de baza.
in jurul nodurilor
grilei de baza.
3.3 Fluxul numeric prin fetele celulei
Principala problema in metodele cu volume finite o
constituie evaluarea fluxului numeric ![]() la interfata
dintre doua celule de integrare. Exista doua variante de calcul
a fluxului numeric la nivelul interfetei: centrat si upwind.
la interfata
dintre doua celule de integrare. Exista doua variante de calcul
a fluxului numeric la nivelul interfetei: centrat si upwind.
Pentru introducerea unor expresii ale fluxului numeric, sa consideram relatia de conservare locala (3), pe un domeniu bidimensional cu o grila structurata ca in fig. 7 [20,21,40,47,68]:
 , (83)
, (83)
unde U este o marime scalara, iar:
![]() ,
, ![]() (84)
(84)
Inlocuind (87) in (83), obtinem:
 (88)
(88)
Avand in vedere relatia (89), schema (88) devine:
 , (90)
, (90)
unde ![]() reprezinta
suprafata celulei (i, j). Deoarece grila este structurata, vom
adopta, in continuare, notatiile specifice acestor grile, ca in metodele
cu diferente finite.
reprezinta
suprafata celulei (i, j). Deoarece grila este structurata, vom
adopta, in continuare, notatiile specifice acestor grile, ca in metodele
cu diferente finite.
Scheme centrate. Raman de
specificat valorile ![]() si
si ![]() , care trebuie sa fie reprezentative pentru
interfata
, care trebuie sa fie reprezentative pentru
interfata ![]() . Evaluarea centrata a fluxului presupune adoptarea unei
discretizari numerice pentru F* din schema (91), care sa
indeplineasca conditiile de simetrie in raport cu
. Evaluarea centrata a fluxului presupune adoptarea unei
discretizari numerice pentru F* din schema (91), care sa
indeplineasca conditiile de simetrie in raport cu ![]() si
si ![]() . In general, pentru o discretizare centrata, pot fi
luate in considerare alternativele urmatoare:
. In general, pentru o discretizare centrata, pot fi
luate in considerare alternativele urmatoare:
Daca pentru calculul fluxului admitem formulele centrate (91):
 (104)
(104)
atunci schema (103) se scrie in forma:
 (105)
(105)
Daca insa estimarea fluxului o vom face cu relatiile (95):
 , (106)
, (106)
atunci schema (90) devine:

(109)
Scheme upwind. Principiul de baza al celei mai simple scheme upwind consta in considerarea fluxului numeric printr-una din fetele celulei egal cu fluxul generat de "celula din amonte". De exemplu, pentru relatia (62) si grilele din fig. 7, estimarea upwind a fluxului numeric se face conform relatiilor:
 (110)
(110)
normala n fiind orientata spre exteriorul celulei (i, j).
 (116)
(116)
Schemele (116) si (7) sunt de ordinul intai de precizie.
3.4 Estimarea gradientului necunoscutelor
In discretizarea cu volume finite, medierea numerica a derivatelor variabilelor (si, implicit, estimarea corecta a valorilor pe fetele celulelor), poate fi facuta prin intermediul teoremei lui Gauss [20,21,40,47,68]:
 (118)
(118)
unde ![]() este frontiera
volumului
este frontiera
volumului ![]() .
.
Pentru celula centrata pe nod, pe baza relatiilor (124), obtinem urmatoarele variante numerice:

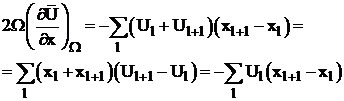
unde insumarea se face pe fetele celulei.
4 Ecuatia de difuzie
Vom exemplifica modalitatea concreta de aplicare a algoritmului numeric general prezentat anterior pentru ecuatia de difuzie in cazul bidimensional:
 (129)
(129)
unde ![]()
Daca pasii retelei sunt constanti si ![]() , se obtine schema:
, se obtine schema:
 (140)
(140)
Daca alegem ca metoda de estimare a fluxului
prin latura generica ![]() o derivata
numerica centrata:
o derivata
numerica centrata:
 , (141)
, (141)
atunci aceasta conduce la:
 (142)
(142)
6 Functionala si ecuatia transferului de caldura in regim nestationar
In problemele de transfer de caldura este util sa se plece de la o forma cunoscuta a functionalei, care apoi se verifica cu ecuatia Euler-Ostrogradski daca conduce la ecuatia diferentiala a transferului de caldura. Daca functionala este verificata, se pune conditia de extrem din care rezulta sistemele de ecuatii algebrice sau diferentiale specifice transferului de caldura [54,63,144].
Sa consideram ecuatia transferului de caldura in regim nestationar:
 (175)
(175)
cu urmatoarele conditii la limita:
a) pe frontiera A1 se impune temperatura T = f(x,y,z) (conditii la limita de tip Dirichlet),
b) pe frontiera A2 are loc un transfer convectiv de caldura cu coeficientul a cunoscut iar temperatura fluidului este T2 de asemeni cunoscuta (conditii la limita de tip Neumann):
 (176)
(176)
c) pe frontiera A3 are loc un transfer de flux q cunoscut (conditii la limita de tip Neumann):
 (177)
(177)
Obtinem:
![]() (186)
(186)
unde ecuatia diferentiala matriciala (186) reprezinta un sistem de ecuatii diferentiale ordinare liniare asociate unui element finit, ceea ce inseamna ca transferul de caldura este liniar atat in regim stationar cat si in regim dinamic.
7 Studiu de caz
Modelarea campului termic pentru transferul termic prin conductibilitate cu metoda elementelor finite. Se considera cazul corpurilor cu simetrie de rotatie.
Pentru analiza cu metoda elementelor finite a corpurilor de rotatie s-a considerat un cilindru cu raza de 5 cm si lungimea de 50 cm (fig.5). Pe suprafata de cota y = 50 cm, temperatura este constanta si egala cu 293 K. Temperatura initiala in tot cilindrul este de 293 K. Pe suprafata de cota z = 0 temperatura este constanta de 1273 K. Se efectueaza o analiza in regim tranzitoriu pe o durata de 1200 s. Datorita simetriei de rotatie se folosesc elemente specifice patrulatere, discretizandu-se un domeniu definit intre axa de rotatie si generatoarea cilindrului.

Fig. 5. Geometria cilindrului
In urma analizei s-a obtinut campul termic in timp, in figura 6 prezentandu-se campul termic dupa 60 s, in figura 7 campul termic dupa 300 s iar in figura 8 campul termic dupa 600 s.

Fig. 6 Campul termic dupa 60 s
In figura 9 este prezentata variatia in timp a temperaturii pentru trei noduri aflate pe axa cilindrului la distanta de 12,5 cm; 25 cm si 37,5 cm fata de originea reprerului (fata cu temperatura mai mare).

Fig. 9. Variatia in timp a temperaturii la distantele de 12,5;25si 37,5 cm
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||
|
|||
Proiecte pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








