
| Biologie | Botanica | Chimie | Didactica | Fizica | Geografie |
| Gradinita | Literatura | Matematica |
Matematica
|
|
Qdidactic » didactica & scoala » matematica Transformata Laplace in calculul operational |
Transformata Laplace in calculul operational
Transformata Laplace in calculul operational
a.Metoda generala a calculului operational consta in urmatoarele:
- data o problema in spatiul original, o transpunem in spatiul imagine. Se fac calculele algebrice din spatiul imagine. Aplicand inversa transformatei Laplace, sau mai comod, utilizand tabelul " f(x) = F(p) obtinem solutia din "spatiul original ". Calculul operational este calculul care utilizeaza transformata Laplace.
b. Problema Cauchy pentru ecuatii diferentiale liniare, cu coeficienti
constanti, rezolvata operational.
Pentru simplificarea expunerii, prezentam lucrurile legate de ecuatia diferentiala liniara de ordinul al doilea, avand coeficientii constanti
![]() -original, cu problema Cauchy:
-original, cu problema Cauchy: ![]()
Solutie: Utilizand
Transformata Laplace, din x(t)=X(p), f(t)=F(p), ecuatia (original) devine: ![]() numita ecuatia
operationala.
numita ecuatia
operationala.
De unde
obtinem X(p) si ![]()
Exemple:
b1. Fie
ecuatia : ![]() cu
cu ![]()
Aratati
ca ![]()
Solutie: ![]()
Ecuatia
operationala este: ![]()
Descompunand in fractii simple obtinem:
![]() De unde:
De unde:![]()
b2. ![]() cu
cu ![]()
R: ![]()
![]()
![]()
b3. ![]()
R: ![]()
![]()
b4. ![]()
R: ![]()
![]() si
si ![]()
b5. ![]()
![]()
R: ![]() de unde:
de unde:
![]()
faza in care putem considera problema rezolvata aproape in totalitate (restul calculelor fiind de rutina si uzura).
c1. Sa consideram initial ecuatia diferentiala liniara cu coeficienti constanti
![]() (1)
(1)
completata cu valorile date:
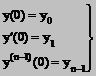 (2)
(2)
b(t) fiind functie original.
Amplificam
ecuatia (1) cu ![]() si integram
in raport cu t de la 0 la
si integram
in raport cu t de la 0 la ![]() .
.
Notand:
![]()
transformata Laplace a functiei y(t), integrand prin parti obtinem:
![]()
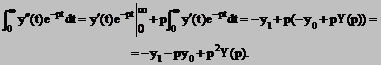 (3)
(3)
|
![]()
Amplificand (3) cu ![]() si insumand
obtinem:
si insumand
obtinem:
![]() (4)
(4)
unde ![]() este un polinom in p
de grad cel mult n-1, R(p) un polinom de grad n si B(p) transformata
Laplace a lui b(t).
este un polinom in p
de grad cel mult n-1, R(p) un polinom de grad n si B(p) transformata
Laplace a lui b(t).
Din (4) obtinem:
![]() (5)
(5)
Functia ![]() verifica ipoteza teoremei D.a.
verifica ipoteza teoremei D.a.
Notand ![]() atunci:
atunci:
![]() (6)
(6)
Dupa cum am luat c, fractia data de (6) are numaratorul de grad cel mult n-2 (termenii de grad n-1 reluandu-se), iar numitorul de grad n+1, deci diferenta de grade intre numitor si numarator este de cel putin 2.
Natura lui B(p)
hotaraste ca functia ![]() sa verifice
conditiile teoremei amintite anterior. Daca gradul lui R(p) este
superior lui 1, este suficient pentru aceasta, B(p) fiind marginita,
ca b(t) sa fie functie original, mai precis sa satisfaca
conditiile:
sa verifice
conditiile teoremei amintite anterior. Daca gradul lui R(p) este
superior lui 1, este suficient pentru aceasta, B(p) fiind marginita,
ca b(t) sa fie functie original, mai precis sa satisfaca
conditiile:
![]() (orig.)
(orig.)
Daca gradul lui R(p) este 1, atunci formula (7) din E.a. arata ca este suficient ca b(t) sa aiba derivata continua pe portiuni satisfacand cu b(t) conditiile (orig.). Deci daca sunt indeplinite conditiile teoremei E.a. cu formula (3) din acelasi paragraf gasim:
![]() (7)
(7)
c2. Sa concretizam cu ecuatia de ordinul doi:
![]()
cu
radacini ale ecuatiei caracteristice complexe ![]() cu
cu ![]() . In electricitate, o astfel de ecuatie descrie
oscilatiile fortate intr-un circuit R, L, C.
. In electricitate, o astfel de ecuatie descrie
oscilatiile fortate intr-un circuit R, L, C.
Trecand la transformata Laplace obtinem ecuatia:
![]()
Rezolvand obtinem:
![]()
si cu formula de inversiune obtinem:
![]()
Notand
![]()
punctele
singulare sunt ![]() si
si ![]() . Pe postul lui
. Pe postul lui ![]() putem alege orice
numar pozitiv. Pentru a calcula integrala completam dreapta
putem alege orice
numar pozitiv. Pentru a calcula integrala completam dreapta ![]() cu o
semicircumferinta de raza
suficient de mare pentru a inconjura toate punctele singulare.
cu o
semicircumferinta de raza
suficient de mare pentru a inconjura toate punctele singulare.
Cu teorema reziduurilor
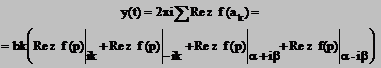
Calculam
reziduul in punctele ![]() fiind poli simpli
pentru f, cu formula:
fiind poli simpli
pentru f, cu formula:
![]()
Procesul
rezultant il constituie suprapunerea a
doua oscilatii - una periodica cu frecventa egala cu
cea a fortei exterioare si cealalta oscilatie fiind
amortizata, viteza de amortizare fiind determinata de ![]() . Pentru
. Pentru ![]() si
si ![]() =k obtinem o rezonanta, iar solutia va fi
o oscilatie cu amplitudinea infinit crescatoare.
=k obtinem o rezonanta, iar solutia va fi
o oscilatie cu amplitudinea infinit crescatoare.
c3. Sa consideram ecuatia caldurii
![]()
pe
intervalul ![]() cu conditiile
initiale
cu conditiile
initiale ![]()
Din punct
de vedere fizic, aceasta spune ca, la momentul t, temperatura nu este
aceeasi in extremitatea initiala si in cea finala ![]() , dar ele se mentin constante. In plus, la momentul
initial, temperatura intr-un punct x este
, dar ele se mentin constante. In plus, la momentul
initial, temperatura intr-un punct x este ![]() .
.
Aplicand transformata Laplace in t, adica trecand de la functia u(x,t) la functia:
![]()
pentru
v(x, p) obtinem: ![]() cu conditiile initiale
cu conditiile initiale ![]() (deci o problema
bilocala). Solutia ei este:
(deci o problema
bilocala). Solutia ei este:
![]() de unde
de unde ![]() care se rezolva
cu teorema reziduurilor.
care se rezolva
cu teorema reziduurilor.
Istoric. Integrala Fourier apare
pentru intaia oara in cartea lui
Fourier "Teoria analitica a caldurii" (1822), unde ea se aplica mai multor probleme de
fizica-matematica. Lucrarile lui Fourier, ca si
lucrarile lui Cauchy care utilizeaza integrala Fourier in studiul propagarii undelor
(1842), nu contin demonstratii de convergenta. Transformata
Laplace este dezvoltata de Laplace in 1812 in Teoria
analitica a probabilitatilor ". Independent,
Euler, in 1737 considera integrale ale produsului ![]() pentru a rezolva
ecuatii ordinare. Nici Euler si nici Laplace nu-si pun problema
utilizarii transformatei in planul complex. Inginerul englez Heaviside,
incepand cu anul 1892, introducand
pentru a rezolva
ecuatii ordinare. Nici Euler si nici Laplace nu-si pun problema
utilizarii transformatei in planul complex. Inginerul englez Heaviside,
incepand cu anul 1892, introducand ![]() gaseste
solutii in problemele de electrotehnica care se reduc la ecuatii
cu derivatepartiale. El pune astfel bazele calculului operational.
Din 1910 Bromwich, apoi Carson, Van der Pol, Doetsch, aplicand transformata
Laplace in complex justifica regulile lui Heaviside.
gaseste
solutii in problemele de electrotehnica care se reduc la ecuatii
cu derivatepartiale. El pune astfel bazele calculului operational.
Din 1910 Bromwich, apoi Carson, Van der Pol, Doetsch, aplicand transformata
Laplace in complex justifica regulile lui Heaviside.
Lucrarile lui Denjoy, Carleman, Ostrovski pe clase de functii quasianalitice se intind in intervalul 1920-1930.
Cu utilizarea integralei Lebesque, teoria transformatei Fourier se dezvolta. Cu dezvoltarea teoriei distributiilor apare posibilitatea definirii transformatei Fourier prin distributii.
(i):f(x) continua pe portiuni
(ii): f(x) nu trebuie sa creasca mai repede ca exponentiala
cand ![]()
(iii): este indeplinita pentru ![]() pentru x > M>0
si in plus, integrala (1) este convergenta pentru
pentru x > M>0
si in plus, integrala (1) este convergenta pentru ![]() Intr-adevar,
Intr-adevar,
![]()
In acest plan, ![]() este functie analitica. Ea este prelungibila
la tot planul si singularitatile sale sunt in
este functie analitica. Ea este prelungibila
la tot planul si singularitatile sale sunt in ![]()
Vom stabili legatura naturala intre denumire si notatie.
Fie deci ![]() astfel incat are sens integrala improprie cu parametru
astfel incat are sens integrala improprie cu parametru
![]() (1)
(1)
Definitie. Daca are
sens (1), F se numeste transformata Laplace a lui f si se mai
noteaza cu ![]() .
.
Transformata fiind definita printr-o integrala improprie, trebuie sa stabilim conditii asupra lui p pentru convergenta. Aceste conditii sunt corelate cu f. Functiile f pentru care exista transformata Laplace se numesc functii original (sau simplu, original), iar transformata Laplace F se numeste functia imagine (sau scurt, imagine). Ca notatii pentru legatura original-imagine pot fi intalnite
![]() sau
sau ![]() sau mai simplu f(x) = F(p), F(p) = f(x).
sau mai simplu f(x) = F(p), F(p) = f(x).
Preferam ultima notatie (putand fi folosite si altele - dupa preferinte si cu conventia stabilita fara ambiguitati).
Numim functie original,
functia ![]() cu
proprietatile
cu
proprietatile
(![]() ) f este nula
pentru
) f este nula
pentru ![]()
(![]() ): f are crestere exponentiala,
adica exista
): f are crestere exponentiala,
adica exista ![]() a si
a si ![]() incat
incat
![]() pentru
pentru ![]() (2)
(2)
Pentru p > a integrala (1) care defineste transformata Laplace este absolut si uniform convergenta.
Intr-adevar, in conditiile (2) avem
![]()
![]()
Ultima integrala este convergenta pentru p > 0 si conform criteriului comparatiei, au loc afirmatiile facute.
In plus, sa observam ca
ipoteza ca ![]() nu este esentiala, argumentarea anterioara
fiind valabila si pentru
nu este esentiala, argumentarea anterioara
fiind valabila si pentru ![]() (in ipoteza (2)).
(in ipoteza (2)).
Cazuri concrete. (d1)
Functia ![]() , cu b real sau complex va avea crestere
exponentiala putand lua a = Reb, M > 1 si
, cu b real sau complex va avea crestere
exponentiala putand lua a = Reb, M > 1 si ![]() Intr-adevar,
Intr-adevar,
![]() (
(![]() )
)
![]() (
(![]() )
)
Deci ![]() si
si ![]() , convergenta integralei avand loc pentru p > Reb
daca
, convergenta integralei avand loc pentru p > Reb
daca ![]() si Rep > Reb
daca
si Rep > Reb
daca ![]()
Observatie. Nu este
greu sa vedem ca ![]() este liniara.
Utilizand liniaritatea, rezultatul din d1 si relatiile lui Euler
este liniara.
Utilizand liniaritatea, rezultatul din d1 si relatiile lui Euler
![]()
![]()
obtinem:
![]() (
(![]() )
)
![]() (
(![]() )
)
pentru ![]() .
.
Proprietatea transformatei Laplace
a.
Daca inegalitatea care exprima proprietatea de crestere
exponentiala este valabila pentru tripletul ![]() pentru orice
pentru orice ![]()
Notand ![]() , a fiind in tripletul
, a fiind in tripletul ![]() ,
, ![]() se numeste abscisa
de convergenta a functiei f.
se numeste abscisa
de convergenta a functiei f.
Din cele facute pana acum
rezulta ca pentru a exista transformata Laplace ![]() este suficient ca f
sa aiba abscisa de convergenta
este suficient ca f
sa aiba abscisa de convergenta ![]() sau
sau ![]() si transformata
are sens pentru
si transformata
are sens pentru ![]() in cazul
in cazul ![]() si
si ![]() in cazul
in cazul ![]() Vom nota cu
Vom nota cu ![]() abscisele de
convergenta pentru f si g.
abscisele de
convergenta pentru f si g.
b. Pentru
![]() are loc proprietatea
de liniaritate
are loc proprietatea
de liniaritate ![]()
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2026 - Toate drepturile rezervate -| |
|
|
|||
|
|||
|
|||
Referate pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








