
| Biologie | Botanica | Chimie | Didactica | Fizica | Geografie |
| Gradinita | Literatura | Matematica |
Matematica
|
|
Qdidactic » didactica & scoala » matematica FISA DE LUCRU - aria triunghiului, criterii De Paralelism, triunghiul isoscel |
FISA DE LUCRU - aria triunghiului, criterii De Paralelism, triunghiul isoscel
FISA DE LUCRU - Aria triunghiului
1 . Calculati aria unui triunghi oarecare care are o latura de 5 dm si inlatimea
corespounzatoare ei , de 32 cm .
2. Aria unui triunghi este de 96 cm² iar una din laturi are 12 cm . Sa se afle
lungimea inaltimii corespunzatoare laturii considerate .
3.Aria triunghiului ABC este 136 cm² , iar inaltimea AD , D apartine BC , are 17 cm . Aflati BC
4. Un triunghi dreptunghic are catetele de 180 mm si 12 cm . Aflati aria triunghiului
5 Demonstrati ca doua triunghiuri cungruente au aceeasi arie .
6. Un triunghi dreptunghic are aria de 684 cm² si inaltimea corespunzatoare ipotenuzei de 36 cm .Aflati ipotenuza triunghiului .
7. In triunghiul ABC , AD este inantime pe BC , iar BE este inaltime pe AC.
a ) Daca BC=6cm ,AD=5 cm ,BE=3cm ,calculati AC ;
b) Daca AD =h , BC = a , AC =b , calvulati BE.
Fisa de lucru
Triunghiul isoscel. Proprietati.
1.Construiti un triunghi isoscel MNP in care MN=MP=6cm si m( M)=50
2.Fie triunghiul isoscel ABC , AB=AC. Aflati masurile unghiurilor triunghiului in fiecare din situatiile urmatoare:
a) m( A)=30
b) m( B)=30
c) m( C)=70
d) m( A)=58
e) m( A)=2 m( B)
f) m( C)= 2 m( A)
3.Calculati perimetrul triunghiului ABC, AB=AC in fiecare din situatiile urmatoare:
a) AB=5 cm , BC=2 cm .
b) AC=10 cm , BC=30 mm.
c) BC=6 cm , AB=3 BC
d) BC=40 mm , AC=2 BC
4.Un triunghi isoscel are perimetrul egal cu
5.Un triunghi isoscel are perimetrul egal cu
6. In figura alǎturatǎ,[AB]≡[AC]≡[BC],m(<DCM)=
m(<DMC)= m(<CDM),

iar M este mijlocul segmentului [BC].Calculati raportul perimetrelor
triunghiurilor ABC si CDM.
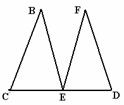
7. Triunghiurile din figura alǎturatǎ sunt congruente si isoscele,cu varfurile
B,respectiv F,iar punctele C,E,D sunt coliniare.
a) Arǎtati cǎ <EFB≡<FBE
b) Demonstrati cǎ punctul E este egal depǎrtat de dreptele BC si DF.
8.In triunghiul isoscel ABC , AB=AC , se construiesc inaltimile BB' si CC'.Demonstrati ca B'C' BC.
9.In triunghiul isoscel ABC , AB=AC se
construieste bisectoarea (AD) , DI(BC).Perimetrul triunghiului ABC este egal cu
|
10.Demonstrati si retineti ca intr-un triunghi isoscel:
a) Medianele corespunzatoare laturilor congruente sunt congruente;
b) Bisectoarele interioare ale unghiurilor congruente sunt congruente.
FISA DE LUCRU
CRITERII DE PARALELISM
1.Pentru figura 1 scrieti toate perechile de unghiuri : alterne interne, alterne externe, corespondente, interne de aceeasi parte a secantei, externe de aceeasi parte a asecantei, opuse la varf si suplementare.
Figura 1 d c

2.Pentru figura 2 scrieti toate perechile de unghiuri congruente si suplementare.
3. In triunghiul ABC , [AD este bisectoarea unghiului BAC , D Є BC. Daca E Є AC astfel incat <DAE≡<ADE. Aratati ca AB ║ DE.
4. Fie un triunghi ABC si D mijlocul laturii [AC]. Pe semidreapta [BD se ia un punct E astfel incatD Є (BE) si DE = BD.Sa se demonstreze ca : a) CE ║ AB ;b) AE ║BC
5. Fie triunghiul ABC si M, N mijloacele laturilor [AB] respective [AC]. Prelungim segmentul [MN] cu segmentul [NP] astfel incat [MN] ≡ [NP]. Demonstrati ca :
a) AB ║ CP . b) NM ║ BC si MN= BC/2.
6. Fie triunghiul ABC si M mijlocul laturii [BC] . Pe semidreapta [AM se considera punctul N astfel incat M Є [AN] si [AM] ≡ [MN]. Demonstrati ca :
a) AB ║ CN .b) AC ║BN.
7. In figura de mai jos, m(<AOB) = m(< ACB) = 100O , 2· m( < BOC) = 3·m( < AOC) si m( < ACO) - m( < BCO) = 20O . Sa se arate ca OA ║ BC.
Fisa de lucru
CLASA A VI-A
a) Definiti dreptele paralele.
b) Enuntati criteriul de paralelism.
- In ∆ABC m ( < A)= 74o , m ( < C)= 48o si AD bisectoarea unghiului BAC. Calculati:
a) m (< B);b) masurile unghiurilor exterioare;
c) masurile unghiurilor formate de AD cu laturile triunghiului.
3. In ∆ABCcu [AB] ≡[AC]masura unghiului exterior din B este 128o. Calculati masurile unghiurilor
triunghiului ABC.
- In triunghiul ∆ABC , BM si CM sunt bisectoarele < ABC si < ACB. Prin punctul M construim
DE ║ BC, D Є AB si E Є AC. Daca BD = 4 cm si CE = 5 cm aflati lungimea segmentului DE.
Fisa de lucru
- a) Definiti unghiul exterior unui triunghi.
b) Enuntati axioma lui Euclid
- In ABC m( < B) = 56o , m ( < C) = 76o si BD bisectoarea unghiului ABC. Calculati:
a) m ( < A) ;b) masurile unghiurilor exterioare
c) masurile unghiurilor formate de AD cu laturile triunghiului
3.In ∆ABCcu [AB] ≡[AC]masura unghiului exterior din A este 114o. Calculati masurile unghiurilor
triunghiului ABC.
4. In triunghiul ∆ABC , AI si BI sunt bisectoarele < BAC si < ABC. Prin punctul I construim
MN ║ AB, M Є AC si N Є BC. Daca AM = 6 cm si BN = 4 cm aflati lungimea segmentului MN.
Triunghiul isoscel
1.Construiti un triunghi isoscel MNP in care MN=MP=6cm si m( M)=50
2.Fie triunghiul isoscel ABC , AB=AC. Aflati masurile unghiurilor triunghiului in fiecare din situatiile urmatoare:
a) m( A)=30 c) m( C)=70 e) m( A)=2 m( B)
b) m( B)=30 d) m( A)=58 f) m( C)= 2 m( A)
3. Calculati perimetrul triunghiului ABC, AB=AC in fiecare din situatiile urmatoare:
a) AB=5 cm , BC=2 cm
b) AC=10 cm , BC=30 mm
4.Un triunghi isoscel are perimetrul egal cu
5.Un triunghi isoscel are perimetrul egal cu
6. In figura alǎturatǎ,[AB]≡[AC]≡[BC],m(<DCM)=
m(<DMC)=

m(<CDM), iar M este mijlocul segmentului [BC].Calculati raportul perimetrelor triunghiurilor ABC si CDM.
7.
Triunghiurile din figura alǎturatǎ sunt congruente si
isoscele,cu
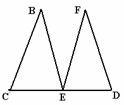
Varfurile B,respectiv F,iar punctele C,E,D sunt coliniare.
a) Arǎtati cǎ <EFB≡<FBE
b) Demonstrati cǎ punctul E este egal depǎrtat de dreptele
BC si DF.
8.In triunghiul isoscel ABC , AB=AC , se construiesc inaltimile BB' si CC'.Demonstrati ca B'C' BC.
9.In triunghiul isoscel ABC , AB=AC se construieste bisectoarea (AD) , DI(BC).Perimetrul triunghiului ABC
este egal cu
10.Demonstrati si retineti ca intr-un triunghi isoscel:
c) Medianele corespunzatoare laturilor congruente sunt congruente;
Bisectoarele interioare ale unghiurilor congruente sunt congruente.
PROPRIETATI ALE TRIUNGHIURILOR. FISA1.
1.Fie triughiul ABC in care :
a) m( A)=44 , m( B)=64
b) m( C)=104 , m( B)=54
c) m( A)=90 , m( C)=31
d) m( A)=m( B)=70
e) m( A)=m( B)= m( C)
f) m( A)=m( B) , m( C)=66
In fiecare situatie determinati masurile tuturor unghiurilor triunghiului.
2.Masurile unghiurilor unui triunghi pot fi exprimate prin (x+10) , (x+30) , (2x-20) , unde x estenumar natural.Determinati cele trei masuri de unghiuri.
3.Determinati masurile unghiurilor unui triunghi stiind ca sunt direct proportionale cu 2,3,5.
4.Fie triunghiul MNP in care m( M)=44 , m( N)=64 .determinati masurile unghiurilor sale exterioare.
5.Sa se determine masurile unghiurilor interioare ale unui triunghi ABC stiind ca doua din unghiurile sale exterioare au masurile de 110 si 140
6.Fie figura 1 .determinati masurile unghiurilor interioare si exterioare ale triunghiului.
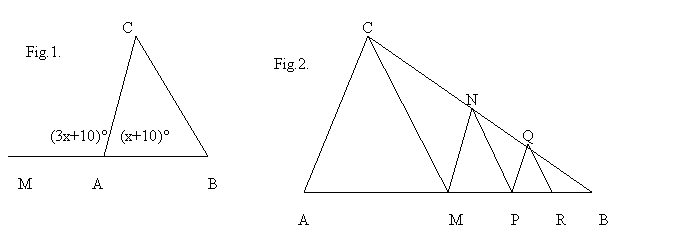
7.In figura 2 AM=MB , MP=PB , PR=RB , CN=NB , NQ=QB. Stiind ca aria triughiuluiMNC este de 16 cm2 determinati ariile triunghiurilor: MNB,MNP,NPB,NPQ,PQB,PQR;QRB,ACM,ABC.
8.Determinati aria unui triunghi in care: b=7cm,h=2 cm.
9.Determinati aria unui triunghi dreptunghic cu
catetele de lungime
10.Determinati lungimea ipotenuzei unui
triunghi dreptunghic stiind ca
lungimile catetelor sunt
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2026 - Toate drepturile rezervate -| |
|
|
|||
|
|||
|
|||
Referate pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








