| Biologie | Botanica | Chimie | Didactica | Fizica | Geografie |
| Gradinita | Literatura | Matematica |
Matematica
|
|
Qdidactic » didactica & scoala » matematica Metoda iteratiilor pentru sisteme de ecuatii algebrice neliniare |
Metoda iteratiilor pentru sisteme de ecuatii algebrice neliniare
Metoda iteratiilor pentru sisteme de ecuatii algebrice neliniare
Fie dat sistemul ecuatiilor cu doua necunoscute
 (3.6)
(3.6)
Se cere determinarea solutiilor reale cu aproximatia data.
Rearanjam sistemul (3.6) in felul urmator :
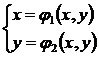 (3.7)
(3.7)
Fie ![]() sunt aproximatii
nule alese arbitrar pentru solutii cautate. Substituind x = x si y = y0 in ecuatia echivalenta (3.7) se
obtine prima aproximatia:
sunt aproximatii
nule alese arbitrar pentru solutii cautate. Substituind x = x si y = y0 in ecuatia echivalenta (3.7) se
obtine prima aproximatia:
 (3.8)
(3.8)
Obtinand x1, y1 si substituindu-le in ecuatia echivalenta (3.7) la fel se obtine a doua aproximatia:
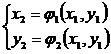 (3.9)
(3.9)
Procedura se repeta pana la determinarea solutiilor xn , yn cu precizia data e
Pentru aproximatie n rezulta formula iterativa:
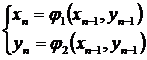 (3.10)
(3.10)
Daca
functiile ![]() si
si ![]() sunt continue
si seriile x1,x2,
. xn si y1,y2, . yn sunt
convergente, atunci limitele lor reprezinta solutii cautate
sunt continue
si seriile x1,x2,
. xn si y1,y2, . yn sunt
convergente, atunci limitele lor reprezinta solutii cautate ![]() si
si ![]() pentru sistemul
(3.7) , respectiv - pentru sistemul
(3.6).
pentru sistemul
(3.7) , respectiv - pentru sistemul
(3.6).
Vom formula fara a demonstra teorema despre conditii de convergenta a procesului iterativ pentru cazul dat.
Teorema : Fie
ca in vecinatatea inchisa R (a≤ x≤ A , b≤y≤B)
exista una si numai una solutie ![]() si
si ![]() a sistemului din doua ecuatii neliniare si atunci, daca :
a sistemului din doua ecuatii neliniare si atunci, daca :
functii ![]() si
si ![]() sunt determinate
si au derivate continui in R;
sunt determinate
si au derivate continui in R;
aproximatii initiale ![]() si toate cele ulterioare
si toate cele ulterioare
![]() (n =1,2 . ) apartin lui R;
(n =1,2 . ) apartin lui R;
iar in vecinatatea R se indeplinesc inegalitati :
![]() ,
,
(3.11)
![]() ,
,
sau
![]() ,
,
(3.12)
![]()
atunci procesul iterativ se converge spre solutia cautata ![]() si
si ![]() .
.
Eroarea de aproximatie pentru iteratia n poate fi apreciata din inegalitatea :
![]() (3.13)
(3.13)
unde: M este numarul maxim din valorile q1 si q2 din conditii (3.11) sau (3.12).
Convergenta metodei iteratiilor se
considera buna daca ![]() sau cand
sau cand ![]() .
.
|
Aplicatia 3.1. Rezolvarea prin metoda iteratiilor a sistemului de ecuatii nelinare
Sa se rezolva cu precizia data ε =0,001, utilizand metoda iteratiilor sistemul din doua ecuatii nelinare:
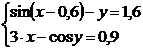
Rezolvare
Rearanjam sistemul, eliminand partial x si y :
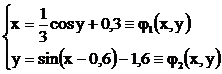
Din analiza
ecuatiilor reiese ca domeniul variabilelor care corespunde ambelor
ecuatii,sau in care sistemul poate
avea o solutie este : 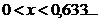 si
si ![]() .
.
Sa verificam convergenta iteratiilor pentru sistemul dat:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Avem ca si inegalitatile: 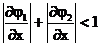 si
si 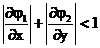 .
.
Astfel conditia de convergenta se indeplineste.
Luam ca valori initiale ![]() ;
; ![]() . Iteratiile se efectueaza dupa formulele :
. Iteratiile se efectueaza dupa formulele :
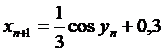
![]()
Rezultatele calculelor se aduna intr-un tabel:
Tabelul 3.1
|
Numarul iteratiei n |
xn |
yn |
xn |
sin(xn-0,6) |
cos yn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Raspuns: x 0,1510 ; y
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2026 - Toate drepturile rezervate -| |
|
|
|||
|
|||
|
|||
Lucrari pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||