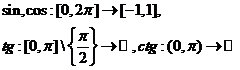| Biologie | Botanica | Chimie | Didactica | Fizica | Geografie |
| Gradinita | Literatura | Matematica |
Didactica
|
|
Qdidactic » didactica & scoala » didactica Planificarea anuala a activitatii didactice - clasa a ix-a |
Planificarea anuala a activitatii didactice - clasa a ix-a
PLANIFICAREA ANUALA A ACTIVITATII DIDACTICE
CLASA a IX-a
Disciplina: Matematica
Clasa: a IX-a
Unitatea de invatamant: Grup Școlar "Constantin Brancuși"Satu Mare
Manualul utilizat: Matematica, Editura Teora Didactica și Pedagogica
Numar de ore pe saptamana: 3 ore.
|
Nr.crt. |
Unitatea de invatare |
Total nr. ore |
Numar ore |
|
Sem. I |
Sem. II |
|||
|
|
Mulțimi și elemente de logica matematica |
|
|
|
|
|
Functii |
|
|
|
|
|
Vectori in plan |
|
|
|
|
|
Coliniaritate, concurența, paralelism calcul vectorial in geometria plana |
|
|
|
|
|
Trigonometrie și aplicații ale trigonometriei in geometrie |
|
|
|
|
|
Evaluare semestriala |
|
|
|
|
|
Recapitulare |
|
|
|
|
|
Total ore |
|
|
|
P L A N I F I C A R E C AL E N D A R I S T I C A
ANUL SCOLAR 2009 - 2010
Clasa a IX-a (3 ore saptamanal)- Semestrul I
|
Nr. crt. |
Unitatea de invatare |
Competențe specifice |
Continuturi |
Nr. ore |
Sapt. |
Obs |
|
|
Multimi si elemente de logica matematica |
1. Identificarea in limbaj cotidian sau in probleme de matematica a unor notiuni specifice logicii matematice si teoriei multimilor Reprezentarea multimilor si a operatiilor logice in scopul identificarii proprietatilor acestora 3. Alegerea si utilizarea de algoritmi pentru efectuarea unor operatii cu numere reale, cu multimi, cu propozitii/ predicate 4. Deducerea unor rezultate si verificarea acestora utilizand inductia matematica sau alte rationamente logice 5. Redactarea rezolvarii unei probleme, coreland limbajul uzual cu cel al logicii matematice si al teoriei multimilor 6. Transpunerea unei situatii - problema in limbaj matematic, rezolvarea problemei obtinute si interpretarea rezultatului |
Multimea numerelor reale: operatii algebrice cu numere reale. |
|
S1 |
|
|
Ordonarea numerelor reale |
|
S1 |
||||
|
Modulul unui numar real |
|
S2 |
||||
|
Aproximari prin lipsa sau prin adaos |
|
S2 |
||||
|
Operatii cu intervale de nr. Reale |
|
S3 |
||||
|
Evaluare |
|
S3 |
||||
|
Propozitie, predicat, cuantificatori |
|
S4 |
||||
|
Operatii logice elementare (negatie, conjunctie, disjunctie, implicatie, echivalenta |
|
S4 |
||||
|
Corelate cu operatiile si relatiile cu multimi (complementara, intersectie, reuniune, incluziune, egalitate); |
|
S5 |
||||
|
Rationament prin reducere la Absurd |
|
S5 |
||||
|
Evaluare |
|
S5 |
||||
|
Inductia matematica. Metoda inductiei matematice ; divizibilitați. |
|
S6 |
||||
|
Demonstrarea unor egalitați, inegalitați, |
|
S6-7 |
||||
|
Probleme aplicative |
|
S7 |
||||
|
Evaluare
|
|
S7 |
||||
|
|
Functii- Șiruri |
1. Recunoasterea unor corespondente care sunt siruri, progresii aritmetice sau geometrice 2. Calcularea valorilor unor siruri care modeleaza situatii practice in scopul caracterizarii acestora 3. Alegerea si utilizarea unor modalitati adecvate de calculare a elementelor unui sir 4. Interpretarea grafica a unor relatii provenite din probleme practice 5. Analizarea datelor in vederea aplicarii unor formule de recurenta sau a rationamentului de tip inductiv in rezolvarea problemelor 6. Analizarea si adaptarea scrierii termenilor unui sir in functie de context |
Modalitati de a descrie un sir; |
|
S8 |
|
|
Siruri particulare: progresii aritmetice, progresii geometrice, determinarea termenului general al unei progresii; suma primilor n termeni ai unei progresii |
|
S8-9 |
||||
|
Conditia ca n numere sa fie in progresie aritmetica sau geometrica pentru n |
|
S9 |
||||
|
Evaluare |
|
S10 |
||||
|
|
Functii- Lecturi grafice |
1. Identificarea valorilor unei functii folosind reprezentarea grafica a acesteia 2.Determinarea solutiilor unor ecuatii, inecuatii utilizand reprezentarile grafice 3. Alegerea si utilizarea unei modalitati adecvate de reprezentare grafica in vederea evidentierii unor proprietati ale functiilor 4.Exprimarea monotoniei unei functii prin conditii algebrice sau geometrice 5.Reprezentarea geometrica a graficului unei functii prin puncte si aproximarea acestuia printr-o curba continua 6. Deducerea unor proprietati ale functiilor numerice prin lectura grafica |
Reper cartezian, produs cartezian, reprezentarea prin puncte a unui produs
cartezian de multimi
numerice; conditii algebrice
pentru puncte aflate in cadrane; drepte in plan de forma x = m sau de
forma y = m, m |
|
S10 |
|
|
Functia: definitie, exemple, exemple de corespondente care nu sunt functii, modalitati de a descrie o functie Egalitatea a doua functii, imaginea unei functii |
|
S11 |
||||
|
Functii numerice f:I |
|
S11-12 |
||||
|
Compunerea functiilor; exemple pe functii numerice |
|
S12 |
||||
|
Evaluare |
|
S13 |
||||
|
|
Evaluare Semestriala |
C1, C2, C3, C4, C5 |
Recapitulare pentru teza |
|
S13-14 |
|
|
Teza |
|
S14 |
||||
|
Discutarea tezei |
|
S14 |
||||
|
|
Vectori in plan |
1. Identificarea unor elemente de geometrie vectoriala in diferite contexte 2. Utilizarea retelelor de patrate pentru determinarea caracteristicilor unor segmente orientate pe configuratii date 3. Efectuarea de operatii cu vectori pe configuratii geometrice date 4. Utilizarea limbajului calculului vectorial pentru a descrie anumite configuratii geometrice 5. Identificarea conditiilor necesare pentru efectuarea operatiilor cu vectori 6. Aplicarea calculului vectorial in descrierea proprietatilor unor configuratii geometrice date |
Segment orientat, vectori, vectori coliniari |
|
S15 |
|
|
Operatii cu vectori: adunarea (regula triunghiului, regula paralelogramului), proprietati ale operatiei de adunare; inmultirea cu scalari, proprietati ale inmultirii cu scalari; conditia de coliniaritate, descompunerea dupa doi vectori dati, necoliniari si nenuli |
|
S15 |
||||
|
|
Coliniaritate, concurenta, paralelism - calcul vectorial in geometria plana |
1. Descrierea sintetica sau vectoriala a proprietatilor unor configuratii geometrice in plan 2. Reprezentarea prin intermediul vectorilor a unei configuratii geometrice plane date 3. Utilizarea calcului vectorial sau a metodelor sintetice in rezolvarea unor probleme de geometrie metrica 4. Trecerea de la caracterizarea sintetica la cea vectoriala si invers) intr-o configuratie geometrica data 5.Interpretarea coliniaritatii, concurentei sau paralelismului in relatie cu proprietatile sintetice sau vectoriale ale unor configuratii geometrice date 6.Analizarea comparativa a rezolvarilor vectoriala si sintetica ale aceleiasi probleme |
Vectorul de pozitie al unui punct |
|
S16 |
|
|
Vectorul de pozitie al punctului care imparte un segment intr-un raport dat, teorema lui Thales (conditii de paralelism) |
|
S16-17 |
||||
|
Vectorul de pozitie al centrului de greutate al unui triunghi (concurenta medianelor unui triunghi) |
|
S17 |
||||
|
Evaluare |
|
S18 |
||||
|
Exerciții recapitulative |
|
S18 |
P L A N I F I C A R E C AL E N D A R I S T I C A
ANUL SCOLAR 2009- 2010
Clasa a IX-a (3ore saptamanal)- Semestrul II
|
Nr. crt. |
Unitatea de invatare |
Competențe specifice |
Continuturi |
Nr. ore |
Sapt. |
Obs |
|
|
Functii- Fucția de gradul I |
1. Recunoasterea functiei de gradul I descrisa in moduri diferite 2. Utilizarea unor metode algebrice sau grafice pentru rezolvarea ecuatiilor, inecuatiilor, sistemelor de ecuatii 3. Descrierea unor proprietati desprinse din reprezentarea grafica a functiei de gradul I sau din rezolvarea ecuatiilor, inecuatiilor, sistemelor de ecuatii 4. Exprimarea legaturii intre functia de gradul I si reprezentarea ei geometrica 5. Interpretarea graficului functiei de gradul I utilizand proprietatile algebrice ale functiei 6. Rezolvarea cu ajutorul functiilor a unei situatii problema si interpretarea rezultatului |
Definitie,
reprezentarea grafica a functiei f :R |
|
S19 |
|
|
Interpretarea grafica a proprietatilor algebrice ale functiei:monotonie, semnul functiei. |
|
S20 |
||||
|
Inecuatii
de forma ax+b |
|
S21 |
||||
|
Pozitia relativa a doua drepte,sisteme de tipul
|
|
S21-22 |
||||
|
Evaluare |
|
S22 |
||||
|
Functii- Funcția de gradul al-II-lea |
1. Diferentierea, prin exemple, a variatiei liniare de cea patratica 2. Completarea unor tabele de valori necesare pentru trasarea graficului functiei de gradul al II-lea 3. Aplicarea unor algoritmi pentru trasarea graficului functiei de gradul al II-lea (prin puncte semnificative) 4.Exprimarea proprietatilor unei functii prin conditii algebrice sau geometrice 5. Utilizarea relatiilor lui Vičte pentru caracterizarea solutiilor ecuatiei de gradul al II-lea si pentru rezolvarea unor sisteme de ecuatii 6. Identificarea unor metode grafice de rezolvare a ecuatiilor sau sistemelor de ecuatii |
Reprezentarea
grafica a functiei f :R |
|
S22-23 |
||
|
Relatiile lui Viete, rezolvarea sistemelor de forma
|
|
S23-24 |
||||
|
Evaluare |
|
S24 |
||||
|
Functii- Interpretarea geometrica a proprietaților funcției de gradul al-II-lea |
1. Recunoasterea corespondentei dintre seturi de date si reprezentari grafice 2. Reprezentarea grafica a unor date diverse in vederea compararii variatiei lor 3. Aplicarea formulelor de calcul si a lecturii grafice pentru rezolvarea de ecuatii, inecuatii si sisteme de ecuatii 4. Exprimarea prin reprezentari grafice a unor conditii algebrice; exprimarea prin conditii algebrice a unor reprezentari grafice 5. Determinarea unor relatii intre conditii algebrice date si graficul functiei de gradul al II-lea 6. Utilizarea monotoniei si a punctelor de extrem in optimizarea rezultatelor unor probleme practice |
Monotonie, punct de extrem (varful parabolei), interpretare geometrica. |
|
S25 |
||
|
Pozitionarea
parabolei fata de axa Ox, semnul functiei,inecuatii de forma |
|
S25-26 |
||||
|
Pozitia relativa a unei drepte fata de o parabola ; rezolvarea sistemelor de forma
interpretare geometrica. |
|
S26-27 |
||||
|
Evaluare |
|
S27 |
||||
|
|
Trigonometrie si aplicatii ale trigonometriei in geometrie |
1. Identificarea elementelor necesare pentru calcularea unor lungimi de segmente si a unor masuri de unghiuri 2. Utilizarea unor tabele si formule pentru calcule in trigonometrie si in geometrie 3. Determinarea masurii unor unghiuri si a lungimii unor segmente utilizand relatii metrice 4. Transpunerea intr-un limbaj specific trigonometriei si geometriei a unor probleme practice 5. Utilizarea unor elemente de trigonometrie in rezolvarea triunghiului oarecare 6. Analizarea si interpretarea rezultatelor obtinute prin rezolvarea unor probleme practice |
Rezolvarea triunghiului dreptunghic. |
|
S27-28 |
|
|
Cercul trigonometric, definirea functiilor trigonometrice:
|
|
S28 |
||||
|
Definirea
functiilor trigonometrice:
|
|
S29 |
||||
|
Formule de reducere la primul cadran Formule trigonometrice pentru : sin(a+b), cos(a+b), sin(a-b), cos(a-b), sin2a, cos2a |
|
S29-30 |
||||
|
Modalitati de calcul a lungimii unui segment si a masurii unui unghi: teorema sinusurilor si teorema cosinusului |
|
S31 |
||||
|
Evaluare |
|
S32 |
||||
|
|
Evaluare semestriala |
C1, C2, C3, C4, C5 |
Recapitulare pentru teza |
|
S32-33 |
|
|
Teza |
|
S33 |
||||
|
Discutarea tezei |
|
S33 |
||||
|
|
Recapitulare finala |
C1, C2, C3, C4, C5 |
Exerciții recapitulative |
|
S34-36 |
|
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||
|
|||
Referate pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||