
| Afaceri | Agricultura | Comunicare | Constructii | Contabilitate | Contracte |
| Economie | Finante | Management | Marketing | Transporturi |
Economie
|
|
Qdidactic » bani & cariera » economie Metoda grafica in studiul economiei |
Metoda grafica in studiul economiei
Metoda grafica in studiul economiei
1. Reflectare de principiu
2. Functii. Definitie
3. Grafice pe sistemul axelor rectangulare
3.1 Grafice, functii si non-functii
3.2 Forma functiei
3.2.1 Drepte si non-drepte
3.2.2 Alte aspecte legate de forma functiilor
3.3 Alte aspecte ale functiilor
3.3.1 Punctele importante
3.3.1.1 Intersectiile si non-intersectiile
3.3.1.2 Punctele de extrem (minim si maxim) si de inflexiune
3.3.2 Dinamica grafica
3.4 Precizari finale, simplificari si clarificari metodologice
3.4.1 Precizari si simplificari metodologico-grafice
3.4.1.1 Graficul abstract
3.4.1.2 Reducerea la graficul "nord-est"(NE)
3.4.1.3 Abstragerea intersectiilor cu axele
3.4.1.4 Inlocuirea curbei propriuzise prin dreapta
3.4.1.5 Exceptii de la indiferenta (X/Y) asupra domeniilor
3.4.2 Cateva conexiuni si corelatii descriptive obligatorii
1. Reflectare de principiu
Economia este inteleasa concomitent drept activitate, stiinta si politica. Evoluam in domeniul stiintei, in ce ne priveste, mai precis al studiului economiei, iar criteriul fundamental sau obiectivul lucrarii de fata este cel de a face inteles obiectul stiintei noastre. Pe scurt, dar si in maniera cea mai semnificativa, vedem economia ca un studiu al relatiei (relatiilor) intre anume fenomene. Complexitatea relatiei creste odata cu numarul fenomenelor si nu numai. Presupunem astfel, ca in schema urmatoare, relatia intre un fenomen socotit determinant (A) si un numar de alte fenomene, notate cu majuscule de la (B) la (I).
Pentru complexitatea aici redata a relatiilor intre fenomene matematica a elaborat notiunea de functie.
2. Functii. Definitie
In definitie, functia presupune insa numai doua multimi sau domenii in corelatie. O corelatie pentru care multimea (A) (spre exemplu, ca in Figura 1) este determinanta, astfel socotita domeniu de definitie - domeniul detrminant -- , vizavi de (B), care este domeniul in care functia ia valori (co-domeniu) -- domeniul determinat. In strictetea acestei logici, pentru oricare element (a), component al domeniului (A), va exista un singur corespondent functional, (b), component al domeniului (B).
![]()
![]() (A)
(A)
(B) (C)
![]()
![]()
![]()
![]()
![]()
![]()
(D) (E) (F)(G)(H)(I)
Figura 1
Se intelege astfel libertatea ca, pentru un anume (b) I (B) sa poata exista mai multi corespondenti functionali de partea domeniului (A). Totodata, daca exista, nu mai multi, ci tot un singur corespondent (a) I (A) al fiecarui (b) I (B) apare ceea ce se numeste caracteristica sau relatia de biunivocitate a aceleiasi functii, care coreleaza domeniile (A) si (B) si astfel corelatia devine si una reciproca.
In ce priveste studiul nostru, nevoile se limiteaza la aceste cunostinte matematice despre multimi - si la aceste cateva randuri, si este bine ca este asa.
3. Grafice pe sistemul axelor rectangulare
Mai precis, putem adauga la schita de idei deja formulata in paragraful anterior, ca domeniile pe care le consideram deja functionale, (A) si (B), pot include multimi de numere, iar aceste numere pot fi si continui, asa cum este multimea numerelor reale (R), sau cea a numerelor reale pozitive (R+), cele mai uzitate domenii in studiul economiei.
O prima observatie, care se ridica odata cu aplicarea functiilor (matematice) in studiul economiei este (cum bine am vazut deja) reducerea corelatiilor fenomenologice specifice la numai doua domenii, (A) si (B), in alternativa carei reduceri am putea considera corelatia intre domeniul (A) si restul domeniilor (fenomenelor, daca discutam pe Figura 1) (B-I).
Metoda grafica - redusa astfel la graficul axelor rectangulare - va urma sa considere:
(i) cele doua domenii, Ox (inlocuind pe A) si Oy (inlocuind pe B) pe cele doua dimensiuni ale planului;
(ii) plus felul corelatiei, figurat grafic in acelasi plan printr-o multime de puncte, cu coordonate perechi, puncte regasind astfel elemente (numere) corespondente intre multimile X (A) si Y(B), ca in Figura 2.
y
. yA.A(xA;yA)
. ..
![]() O xAx
O xAx
. .
Figura 2
Si am exemplificat aici punctul A, oarecare, ca semnificand numarul (xA), inclus in mutimea (X) si corespunzator numarului (yA), inclus in multimea (Y).
Alta observatie se leaga de faptul ca, daca consideram lucrurile ca in Figura 2 - si astfel le vom considera de aici inainte --, mai apare detaliul dupa care cele doua domenii functionale nici macar nu difera literalmente intre ele, ci ambele apartin multimii numerelor reale (R). Faptul este insa si unul necontradictoriu, contrar aparentelor, ca si unul neesential, in partea interesului studiului nostru. Iar aceasta pentru ca vom regasi, in spatele aceleiasi multimi numerice - desfasurate pe doua dimenisuni, adica pe abscisa (Ox/orizontal) si pe ordonata (Oy/vertical) - de cele mai multe ori marimi fizice diferite, corespunzatoare unui fenomen sau altuia.
3.1 Grafice, functii si non-functii
Continuand insa si ideea notata la prima observatie, metoda noastra grafica se vede suferinda vizavi de studiul economiei, odata ce ea Totusi, mai este bine sa realizam - aici rupandu-ne de canoanele matematicilor si matematicienilor - si alte lucruri elementare, cum ar fi:
Faptul ca in studiul nostru cele doua multimi, (X) si (Y), pot fi vazute mai mult sau mai putin in raporturile de determinare de la (X) catre (Y), si nu invers. (Y) poate fi tot atat de bine, la randul sau, determinant pentru (X). Iar daca, spre deosebire de cele aratate in Figura 2, functia apare sub forma curbelor (adica locurilor geometrice, calitate decurgand din continuitatea punctelor componente), studiile noastre pot viza si ceea ce - plecand de la definitie - matematica intelege drept non-functie de (X) - Figura 3/c.face apel la functiile si graficele matematicilor analitice - si este bine sa tinem seama si de acest lucru inca de la plecare.
![]()
![]()
![]()
Oy yOy


 f(a)f(b)f(c)
f(a)f(b)f(c)
![]()
![]()
![]()
O Ox O Ox O Ox
(a) (b) (c)
Figura 3
Astfel, daca si studiul economiei contine rigoarea dupa care un fenomen este cel determinant, totusi domeniul de definitie nu este totdeauna figurat pe abscisa, ci poate apare si pe axa ordonatelor.
In urmatorul rand, asa cum vom dezvolta si in cele ce urmeaza, graficul din economie mai pastreaza si alte resurse in favoaarea extinderii studiului de la relatia restransa intre numai doua multimi de elemente:
(i) fie, prin calitatea sa de loc geometric, curba (functia) poate corespunde unui singur numar, contabilizat intr-o terta dimensiune (Z, alta decat X si Y);
Exemplu: costurile de productie se exprima, in ultima instanta, in unitati fizice apartinand factorilor de productie - adica capitalului (k), prin care intelegem deocamdata dotarea tehnica a productiei, si muncii (L), ca in Figura 4. Ceea ce nu poate insa pierde din vedere expresia costurilor si in unitati monetare, unificatoare si facand comparabile unitatile fizice ale diferitilor factori intre ele. Pe de alta parte, factorii de productie au in vedere si inter-substitutia lor (Lectia I), respectiv maniera in care o unitate de capital (k) este (poate fi) inlocuita de un numar de unitati de munca (L) pentru a lasa invariabil nivelul aceluiasi cost total (C) - vezi Figura 4/a & b.
![]()
![]() k C
k C
(a) (b)
![]()

 k1 C1
k1 C1
 kA A
kA A
![]()
 k1k
k1k
kB B (Z)
(Z)
![]()
![]()
O LA LB L1 L O L1 L
Figura 4
(ii) fie, avand in vedere intregul itinerar determinant din Figura 1 (la care astfel revenim), o terta determinare asupra corelatiei intre elementele lui (X) si lui (Y) poate aduce "deplasarea" curbei - catre stanga, respectiv dreapta, cu regasirea unei curbe perfect paralele, pe care coordonatele (Ox) si (Oy) sunt si ele altele.
Exemplu: functia cererii unui bun oarecare, (x), adica (Dx), Lectia II, este vazuta ca o relatie descrescatoare intre cantitatea (oferta) de bun (x), (Qx), si pretul aceluiasi bun pe piata, (Px). Economistii vad, de fapt, determinarea pretului asupra cantitatii, in vreme ce uzanta face ca (Px) sa fie notat pe ordonata, iar (Qx) pe abscisa. Cu toate acestea, indiferent care dimensiune variaza, avem de a face cu miscarea de-a lungul curbei cererii - vezi Figura 5/a - intre punctele A(Qa;Pa) si B(Qb;Pb). Daca insa are loc initial o crestere a venitului consumatorului ( Y), iar venitul consumatorului, ca marime, nu este inclus in dimensiunile (domeniile) graficului, vom regasi deplasarea curbei cererii catre dreapta - vezi Figura 5/b - respectiv inducerea de crestere atat pentru cantitate cat si pentru nivelul pretului.
![]()
![]()
![]()
 P
P PA
A
(D) (D') (D) PA' A'
P
P PA
A
(D) (D') (D) PA' A'
PAA
![]()
PB B
![]()
![]() O QA QB Q O QA QA' Q
O QA QB Q O QA QA' Q
(a) (b)
Figura 5
3.2 Forma functiei
Daca, prin cele aratate, metoda grafica aplicata in economie se desparte de matematica atat pe calea simplificarilor, cat si pe aceea a plusului de concretete, totusi sa subliniem simplificarile care raman ale noastre. Lasam astfel sa se confunde metoda grafica cu graficele rectangulare, ca si functia cu graficul care o reflecta pe planul axelor rectangulare. Graficul va reflecta, de aici incolo, puncte, curbe si suprafete semnificative - aceeasi ordine si pentru inter-determinarea acestor componente. Curbele, ca si suprafetele, determinari ale punctelor componente, capata forme, asa cum vom dezvolta incontinuare.
3.2.1 Drepte si non-drepte
Suntem in fata primei sub-impartiri, care apare drept una de bun simt vizionar - astfel, criteriul nici nu mai merita numit - iar mai apoi una de substrat matematic evident. Evident, in planul axelor rectangulare, orice dreapta - in alta expresie, functie rectilinie - apare ca o functie explicita de felul:
y = ax + b
iar implicita de felul:
mx + ny +p = 0
Strictetea functiei rectilinii se vede, de cealalta parte, adica de partea curbelor propriuzise - functiilor non-rectilinii, in cealalta exprimare - in fata unei liste mai lungi a tipurilor de functii (matematice), tipologie care urmeaza firesc o lunga discutie matematica.
Studiul grafic al economiei urmeaza insa o alta cale decat cea matematica. In cazul de fata, functiile rectilinii (dreptele) si non-rectilinii (curbele) sunt considerate pe picior de egalitate, despartirea intre cele doua categorii avand loc pe cel putin trei criterii mai interesante pentru economie (Tabelul 1).
Tabelul 1
Functii rectilinii si non-rectilinii
|
NR. |
CRITERIU |
FUNCTIA |
|||||
|
RECTILINIE |
NON-RECTILINIE |
||||||
|
1. |
Variatia legaturii intre variabile |
Stransa |
Relaxata |
||||
|
2. |
Panta (tangenta unghiului cu axele) |
Fixa
|
Variabila |
||||
|
3. |
Intersectia cu axele |
Obligatorie |
Cazuala |
||||
![]()
![]() y y
y y

 C
C
 (f) (f)
(f) (f)
![]()
![]()
 A B
A B
![]()
![]()
![]()
![]()
![]() a
a
![]()
![]() a1 a2a3
a1 a2a3
O (a) rectilinie x O (b) non-rectilinie x
(dreapta) (curba propriuzisa)
Figura 6 Forma functiilor
A pune pe picior de egalitate cele doua tipuri de functii reprezinta, fara doar si poate, o simplificare colosala din punctul de vedere al matematicii. Odata cu acest lucru, esenta studiului economiei prin metoda grafica se fundamenteaza pe geometrie si vizualizare, mai mult decat prin explicitare prin formule matematico-analitice. Cu toate acestea, am putea zabovi putin asupra numai catorva formalizari - cu atat mai mult cu cat o facem numai aici, vezi Figura 7.
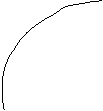
Figura 7 Diverse functii non-rectilinii tipice

![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() y y y (f/a) (f/b) (f/c)
y y y (f/a) (f/b) (f/c)
![]()
 O x O x O x
O x O x O x
(a) (b) (c)
y y

O x O x
(d) (e)
|
|
(a) |
Parabole: |
y = ax2+bx+c |
|
|
(b) |
Curba polinomiala de gradul trei: |
y= ax3+bx2+cx+d |
|
|
(c) |
Hiperbola dubla: |
ax2+by2 = 0 |
|
|
(d) |
Curba exponentiala: |
y= ax |
|
|
(e) |
Curba logaritmica: |
y=logx a |
3.2.2 Alte aspecte legate de forma functiilor
In acest sub-paragraf discutam despre ceea ce formeaza intimitatea studiului grafic al curbelor - suplinind simplificarea fata de viziunea matematica. Mai intai, forma functiilor se conecteaza obligatoriu si semnificativ la ceea ce se numeste panta, respectiv tangenta la functie. Intelegem aici ambele semnificatii ale tangentei (pantei): (i) valoric -- valoarea raportului intre latura opusa si cea alaturata, in cadrul triunghiului dreptunghic, o valoare crescatoare, odata cu unghiul propriuzis; (ii) grafic -- dreapta care intersecteaza curba (functia), intr-un punct anume, in speta, punerea in evidenta a unghiului acesteia cu axa absciselor.
Panta apare:
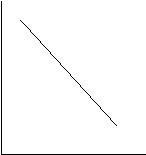
(i) crescatoare - punand in evidenta corelatia intre marimile (X) si (Y) in crestere concomitenta - respectiv descrescatoare - aspect care sugereaza cresterea uneia dintre marimi pe seama descresterii celeilalte;
(ii) abrupta, respectiv lenta - indicand cresterea / descresterea drept mai evidenta (aproape de verticala) sau mai lenta (aproape de orizontala).
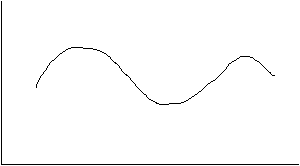
In randul urmator, apare un aspect legat tot atat de panta, cat de forma curbelor, cel al consecventei sau inconsecventei in caracterul crescator sau descrescator al pantei, in translatia acesteia de-a lungul (punctelor) curbei. Deosebim astfel curbele monotone -- care raman crescatoare sau descrescatoare in totalitate - de cele nemonotone care prezinta, in puncte diferite, cresteri urmate de decresteri si-sau invers Dreptele (functiile rectilinii) formeaza chiar primul exemplu de curbe monotone, cu particularizarea ca ele se prezinta nu numai monoton crescatoare sau descrescatoare, ci si egal crescatoare-descrescatoare. Curbele propriuzise pot fi monotone, pastrandusi cresterea sau descresterea pe intregul parcurs, dar, spre deosebire de drepte, cresterea-descresterea le este, la randul ei, crescatoare sau descrescatoare.
In distinctia curbelor nemonotone de cele monotone opereaza de facto diferentierea formalizarilor matematice, surprinsa mai sus in Figura 7. Respectiv, un singur tip de functii se expune grafic crescator-(si)-descrescator - am numit functia polinomiala[1]. Specificul acestei functii se leaga si de aspecte ce urmeaza, deasemenea, sa le discutam[2]
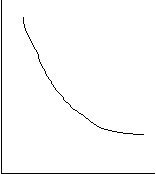
Astfel, un al treilea aspect in ordine defineste tot legatura dintre panta si forma, facand-o intr-un mod inca mai subtil - am numit aici convexitatea versus concavitatea functiilor monotone. O curba este convexa, cand varful (mai corect bombeul) ei este catre origine, dupa cum este concava cand acelasi bombeu se prezinta in partea opusa originii. Convexitatea si concavitatea indica modul in care evolueaza panta monoton crescatoare / descrescatoare de-a lungul curbei. Respectiv, aspectul este important atat prin accelerarea sau decelerarea cresterii, cat si pentru functiile care indica substitutii intre domenii.
De observat din nou ca aceleasi functii ne-monotone sunt - odata cu definitia care le face succesiv crescatoare si descrescatoare - si succesiv convexe si concave - am numit din nou functiile polinomiale.
Figura 8 Forme si pante ale functiilor
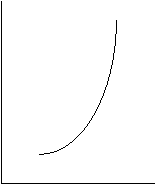
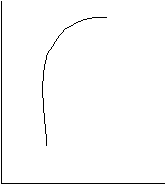
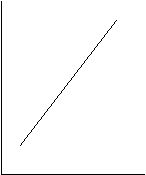

y y y
(a)
O x O x O x
(a1) (a2) (a3)
y y y
(b)
O x O x O x
(b1) (b2) (b3)
Oy
(c)
O x
(a) crescatoare (a1) dreapta (a2)abrupta (a3)incetinita
(b) descrescatoare (b1)dreapta (b2) abrupta (b3) incetinita
(c) crescatoare - descrescatoare
3.3 Alte aspecte ale functiilor
Discutam despre alte doua aspecte, anume punctele importante si dinamica grafica.
3.3.1 Punctele importante
Ordinea in care discutam despre puncte importante tine din nou de diferentierea metodei grafice de matematica analitica. Pentru cea din urma, fiecare punct al curbei este unul important. Pentru analiza pur grafica, dimpotriva, intereseaza prioritar vizualizarea curbelor - sau ceea ce numim graficul abstract. Fapt pentru care opereaza si a doua distinctie, aceea intre curbele monotone si cele nemonotone, apoi aceea intre curbele care intersecteaza si cele care nu intersecteaza axele. Insfarsit, intersectiile se pot regasi, nu numai cu axele, ci si intre curbe diferite.
Ca atare, regasim pe grafice distinctia esentiala a putinelor puncte importante, dupa cum prezenta punctelor importante este una facultativa, pe graficele rectangulare de studiu al economiei.
In ce priveste probelmele (aplicatiile) de constructie grafica, identificarea punctelor importante este prioritara trasarii curbelor - ele vor functiona drept "puncte de fixare" a acestora. Corespunzator, constructia curbelor date drept lipsite de puncte importante este una cu atat mai libera de orice constrangere dimensionala - cu exceptia, buninteles, a constrangerii date de forma curbei.
3.3.1.1 Intersectiile si non-intersectiile
Intersectiile sunt, asa cum este deja sugerat, de doua feluri. De o parte, intersectarile axelor rectangulare, de cealalta intersectarile curbelor (functiilor) intre ele - pentru situatia curbelor multiple pe unul si acelasi grafic rectangular.
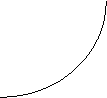
Intersectarile cu axele (Figura 9) sunt obligatorii cel putin pentru drepte (curbe rectilinii), dar si pentru alte curbe. Concomitent, este totusi posibil ca dreapta sa formeze doua intersectii cu axele (cazurile uzuale), sau numai una, atunci cand ea este paralela la una dintre axe.
![]()
![]() Y y y
Y y y

![]()
![]()
![]()
![]()
![]() O x O x O x
O x O x O x
Figura 9 Intersectii cu axele
Or, din nou, diferenta intre dreptele ordinare si cele paralele cu axele este deosebit de semnificativa - o dreapta paralela cu una dintre axe practic anjuleaza corelatia functionala intre domeniile (X) si (Y); in vreme ce, fireste, dreptele ordinare pastreaza corelatia cu specificul constantei valorii acesteia.
Aspectul intersectiei simple versus duble, de care am vorbit aici, este insa unul specific dreptelor. In realitate, intersectarea axelor inseamna altceva in termenii general semnificativi - termeni prioritari fata de forma curbelor in discutia intersectiei cu axele:
(i) Intersectarea axei Ox este totuna cu anularea valorii de pe axa Oy(Y), respectiv cu solutiile ecuatiei (Y=0). Aceste intersectii se vor regasi in puncte de coordonate (x) (solutiile lui Y=0) si respectiv zero - exemplu: A (a;0).
(ii) Dimpotriva, intersectarea axei Oy echivaleaza anularii valorii de pe axa Ox (X), respectiv termenului (coeficientului) liber de (x) si (y) din expresia matematica a curbei (functiei). Aceste intersectii se vor regasi in puncte de coordonate zero si respectiv valoarea termenului (coeficientului) liber al functiei - exemplu: A(0;a).
Semnificatia grafica priveste insa in alta parte. Daca consideram, ca in situatiile uzuale, domeniul (X) drept determinant (exogen) fata de (Y) determinat (endogen), atunci vom cauta in intersectia cu axa Ox valoarea exogenei care induce anularea endogenei, iar in intersectia cu Oy pe aceea a endogenei neinfluentate de exogena.
Intersectarile inter-functii, la randul lor, sunt atribuite exclusiv curbelor multiple, respectiv a doua sau mai multe functii reflectate pe acelasi grafic. Punctele (importante) de intersectare a functiilor se vor regasi, fireste, in coordonate (x;y) satisfacand ambele functii, practic egaland cele doua expresii functionale, atat pentru (x) cat si pentru (y). Intr-o astfel de ordine, intersectarea axelor devine un caz particular al intersectiilor inter-functii, in sensul in care functia data (intersectata) este adusa la echivalenta cu curbele y = 0, sau x = 0, dupa caz. Intersectiile inter-functii identifica, uzual, puncte - identificate prin perechi de coordonate - de echilibru sau eficienta.
Non-intersectiile identifica situatiile de comportament asimptotic. Curbele, la extremitati, se pot apropia tendential de o dreapta oarecare, respectiv de una dintre axe. Pot fi asimptotice chiar de ambele axe, dovedind comportament asimptotic la ambele extremitati. Regasim in comportamentul asimptotic functii care tind catre anume coordonate, respectiv valori, fara insa a (putea) fi definite exact pentru acestea. Exemplele cele mai la indemana tin tot de raporturile fata de axe. O curba asimptotica fata de Oy este, in ordinea logico-matematica in care am identificat intersectarea aceleiasi axe, una a imposibilitatii (matematice) a anularii valorii (x) exogenei; aceeasi situatie pentru anularea valorii (y) la asimptotica fata de axa Ox. In limbaj matematic, functia nu este definita pentru intersectarea axei (axelor), respectiv in limbaj mai concret intersectia (axei) nu are loc pentru valori finite ale acestei axe.
In Figura 10(a), curba izocuanta (izo-productie in materia factorilor capital /k si munca/L combinati) este prin definitie asimptotica fata de ambele axe - intersectarea axelor ar fi insemnat ca o productie sa poata fi, realmente, sau complet automatizata (Ok), sau complet manuala (OL). In cazul (b), curba cererii fata de pret a bunului (x) ar intersecta axa pretului (OPx) pentru un nivel finit al pretului care ar face bunul nevandabil, iar axa cantitatii (OQx) pentru o oferta a bunului (x) capabila sa anuleze acestuia valoarea (pretul) pe piata etc.
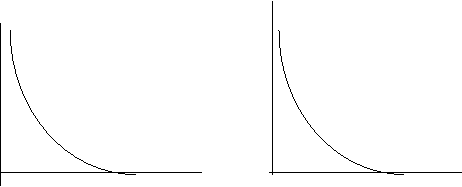 Px
Px
k
(Q) (Dx)
O L O Qx
Figura 10 Non-intersectii cu axele
3.3.1.2 Punctele de extrem (minim si maxim) si de inflexiune
Acestea apartin functiilor ne-monotone - in speta, restranse la expresia polinomiala (Figura 11).
![]() y
y
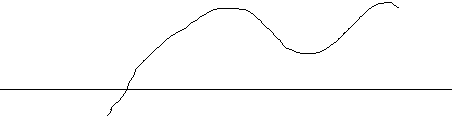
O x1 x2 x3 x4 x5 x6 x7 x
Figura 11 Functie cu minime si maxime
(polinomiala)
Care expresie confera insa functiei, asa cum am descoperit mai sus, dubla calitate de crescatoare-descrescatoare si convexa-concava.
Punctele de extrem sunt cele de maxim si respectiv minim. Ceea ce identifica coordonate pentru care functia isi schimba panta crescatoare in descrescatoare (maxim), respectiv panta descrescatoare in crescatoare (minim)[3]. Punctele de inflexiune, de cealalta parte, apartin in exclusivitate aceleiasi categorii de curbe, iar coordonatele lor alterneaza celor ale punctelor de extrem, atat pe dimensiunea Ox, cat si pe cea Oy. Sunt acele puncte in care functia devine din convexa concava si invers.
Rudenia intre cele doua categorii de puncte importante este una care incepe cu situarea lor pe una si aceeasi curba si continua cu descoperirea lor drept solutii ale derivatelor functiei - de ordinul intai pentru punctele de extrem; de ordinul al dilea pentru punctele de inflexiune[4]. Din Tabelul 2 extragem astfel comportamentul functiei polinomiale.
Tabelul 2
Caracterizarea comportamentului functiei cu maxime si minime
din Figura 11
|
X |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
|
y'(x) |
|
|
0 |
|
0 |
|
0 |
|
y''(x) |
|
0 |
|
0 |
|
0 |
|
|
y(x) |
(0)& |
|
M(1) |
|
m(1) |
|
M(2) |
|
y(x) |
(0) & Cx |
I(1) |
Cv |
I(2) |
Cx |
I(3) |
Cv |
Legenda:
-- functie crescatoare
-- functie descrescatoare
Cv - functie concava
Cx - functie convexa
I(i) - puncte de inflexiune, in ordinea (i)
m - puncte de minim
M (i) - puncte de maximm in ordinea (i)
(0) - anularea valorii y(x) / intersectia cu axa Ox
3.3.2 Dinamica grafica
Este, in general, de doua feluri:
(a) de-a lungul curbei date - dinamica indusa de variatia exogena a uneia dintre dimensiunile date de axe. De o parte, dinamica pe una dintre dimensiuni induce automat pe aceea a celeilalte dimensiuni, de cealalta, aceasta (deja) dubla dinamica respecta regula dictata asupra configuratiei curbei (Figura 12).
y

yA A
yB B
![]() O xA xB x
O xA xB x
Figura 12 Dinamica de-a lungul curbei
(b) a curbei in intregime - dinamica indusa de variatia unei terte variabile. Curba "se deplaseaza" in sensul in care ia nastere (pe directia deplasarii ei) o alta curba, perfect paralela si astfel paralela si izomorfa cu cea dintai. Dupa modul in care s-a exercitat deplasarea curbei, astfel, fiecarui punct de pe curba initiala ii va corespunde altul, aflat pe noua curba.
Ceea ce necesita a adauga faptul ca functia redata aici prin curba cunoaste si alte exogene decat ceea ce indica dimensiunile axelor. Astfel, de o parte, dinamica prin deplasarea curbei se abate de la regulile deplasarii de-a lungul curbei in materie de dinamica a coordonatelor punctelor, de cealalta, metoda grafica dobandeste aici calitatea redarii unei dimensiuni adaugate celor doua deja explicitate pe axele graficului (Figura 13).
y
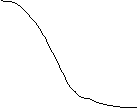
![]()
![]()
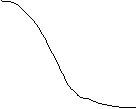
![]()
![]() O x
O x
Figura 13 Dinamica curbei in intregime
Concret, este deosebit de important ca, inspre exemplificare:
curba productiei pe termen scurt, redata in raport direct de factorii variabili (munca sau capital variabil, Lectia I), sa poata fi vazuta concomitent in legatura cu capitalul constant;
curba productiei pe termen lung (izocuanta) sa apara redata alaturi de dimensiunile factorilor munca si capital tot pe graficul cu numai doua dimensiuni (Lectia I);
idem, nivelul costurilor sa poata aparea si el alaturi de reprezentarea sa directa in unitati ale celor doi factori de productie (curba izocost, Lectia I);
curba cererii, fata de pret, sa poata fi studiata concomitent si in raport de alte variabile (Lectia II) etc.
Dinamica curbei in intregime se defineste, in aceste conditii, in directa legatura cu ceea ce s-ar putea numi reprezentarea indirecta a tertei dimensiuni pe graficul plan (de doua dimensiuni).
3.4 Precizari finale, simplificari si clarificari metodologice
In cele de mai sus am pus bazele metodologice ale abordarii grafice a fenomenelor economice. Suntem, de aici incolo, capabili sa intelegem un grafic deja construit si sa construim un grafic la indicatii literale, dupa care sa tragem concluziile ce se impun. Am pornit de la premisele matematice ale chestiunii (metodei) noastre, apoi ne-am despartit de rigorile matematice.
Aceasta din urma strategie - vezi aici:
(i) despartirea de expresia matematica a functiei;
(ii) indiferenta de principiu in situarea multimilor (X) si (Y) in pozitia de exogen/endogen;
(iii) considerarea pe picior de egalitate a curbelor rectilinii (dreptelor) cu cele curbilinii propriuzise (toate functiile matematice elementare);
(iv) abstractia de caracterul polinomial al functiilor cu puncte de extrem si de inflexiune
a mers in favoarea a ceea ce ofera metodei grafice mai multa individualitate, rivalizand cu aceea a matematicii. Din perspectiva matematica, graficul se lasa calculat si determinat, in vreme ce din perspectiva vizuala el se personalizeaza, "explica" si se lasa citit, simplifica viziunea in favoarea observatiei stiintifice, dar si concrete si astfel corecte.
Ruperea de rigorile matematice isi plateste pretul, printre altele, si cu descoperirea altor rigori, nu tocmai simple nici acestea. Iar lipsa rigorilor lasa sa se descopere si unele imperfectiuni, lipsuri si limite, uneori inducand in eroare pe observator. Nicio metoda de studiu nu e perfecta, nici metoda grafica nu este.
Dar o certitudine ramane pe partea favorabila a lucrurilor. Daca cel ce studiaza economia prezinta deficiente, sau chiar "alergie", la dezvoltarile matematice - lipsuri tot atat prezente la unii oameni de specialitate - el are totusi o sansa. Am numit aici alternativa de a intelege aceasta specialitate dupa rigori (totusi) stiintifice si logice - respectiv altfel decat dupa expunerile traditionale din manualele de economie. Iar virtutile metodei grafice au si facut-o pe aceasta deosebit de aplicabila in universitatile occidentale.
Continuand insa ideea dupa care si metoda grafica mai poate - fie si prin capacitatea ei vizionara - complica lucrurile pe alocuri, putinele generalitati ce le mai avem de adaugat aici se vor referi mai intai la cateva operatii simplificatoare, apoi la cateva silogisme de principiu nelipsite instrumentarului observatorului. Dupa toate aceste clarificari finale nu ar mai putea urma decat aplicatiile propriuzise, cu particularitatile fiecareia.
3.4.1 Precizari si simplificari metodologico-grafice
Ideea de la care pornim este aceea ca un grafic expus corect este si unul complet, an sensul in care acesta sa contina toate elementele, atat date (exogene) cat si rezultate (endogene). Sa facem insa o paralela intre acest studiu, destinat celor ce se initiaza, si demersul stiintei economice, in profunzimea cercetarii ei. Din acest ultim punct de vedere, sa ne amintim ca economia ca stiinta nu beneficiaza de instrumentarul riguros si nu o data direct al stiintelor exacte. Respectiv, ii ramane apropierea de obiectul ei de cercetare prin teorii si modele. Modelul este simplificarea unei realitati mult mai complicate ca principiu si realitate. El lucreaza astfel in favoarea explicitarii sale si intelegerii unei esente fenomenologice.
Tot atat putem intelege metoda grafica simplificand, prin sine-insasi, aceeasi realitate pentru a o explica. Dupa care, grafica se simplifica si pe sine-insasi, in absolut acelasi scop si aceeasi ordine. In lipsa a astfel de simplificari avansate, graficele ar fi expuse sa devina complicate, greu de descifrat si riscand sa isi piarda chiar propriul principiu de concepere.
3.4.1.1 Graficul abstract
Subintelege o limita a studiului grafic, dupa care:
in loc de a porni vreodata de la puncte de referinta pentru a deduce forma si felul functiei - ceea ce face obiectul unei discipline separate si bine individualizate, am numit econometria;
dimpotriva, pornim de la functii de forma cunoscuta, de specificitate si rigoare tot atat cunoscute in prealabil, si suntem mai putin interesati de dispunerea punctelor proprii curbei (coordonatelor exacte ale acestora).
Acesta este principiul aplicabil pana la limita existentei punctelor importante - vezi intersectii, non-intersectii, puncte de extrem si de inflexiune, ca in subparagraful 3.3.1, de mai sus.
3.4.1.2 Graficul abstract
A fost deja operata in cele mai multe dintre graficele exemplificative deja expuse pana aici. Este o alta simplificare mergand in profunzimea definirii domeniilor (X/Y), pe aceeasi multime a numerelor reale (R). Apoi ea tine seama si de situarea evaluarilor economice in valori pozitive, in partea lor covarsitoare, destul de rar negative. Tot in parte covarsitoare, deci, graficele noastre isi vor defini axele pe multimea numerelor reale pozitive (R+).
3.4.1.3 Abstragerea intersectiilor cu axele
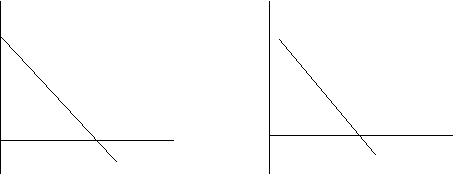
Poate avea loc ori de cate ori aceste intersectii sunt lipsite de continut si semnificatie concrete, in contextul aplicatiei. Nu se confunda, bineinteles, cu comportamentul asimptotic, respectiv cu non-intersectia cu axele (Figura 14), ci abstragerea opereaza asupra semnificatiei intersectiilor - a valorii endogenei neinfluentate de exogena (Oy), respectiv a valorilor exogenei care o anuleaza pe cea a endogenei (vezi si 3.3.1.1, de mai sus).
 y y
y y
(fa) (fb)
O x O x
(a) (b)
Figura 14 Intersectarea axelor (a) si abstragerea intersectiei cu axele (b)
Implicit, aceasta abstragere este inteleasa in sensul in care, in acelasi context al aplicatiei, semnificatia vizeaza alte aspecte. Limita aplicarii acestei simplificari este data de functiile pentru care intersectiile cu axele sunt caracteristica esentiala - vezi exemplul hiperbolei concave pentru limita productiilor (Lectia IV).
3.4.1.4 Inlocuirea curbei propriuzise prin dreapta
Este posibila pe acelasi criteriu al eludarii importantei formei curbe a functiei - respectiv a relaxarii legaturii dintre variabile, mai concret eludarea, ca neesentiala, a situatiei in care o variabila creste /scade mai accentuat decat cealalta (Figura 15). Ideea este aceea ca dreapta este mai lesne de observat si de studiat atat grafic cat si geometric si numeric (matematic).
 y y
y y
(fa) (fb)
O (a) x O (b) x
Figura 15 Inlocuirea curbei propriuzise (a) prin dreapta (b)
Limitele si ale acestui tip de simplificare se fac simtite acolo unde, fireste, convexitatea /concavitatea sau nemonotonia curbei, insotita de identitificarea obligatorie a punctelor de extrem si de inflexiune, sunt esentiale.
3.4.1.5 Exceptii de la indiferenta (X/Y) asupra domeniilor
Plecand de la indiferenta asupra expunerii domeniului de definitie pe abscisa si a celui in care functia ia valori pe ordonata - procedura obligatorie in partea matematica - economistii s-au obisnuit sa noteze:
(i) cantitatile, pe abscisa;
(ii) preturile, pe ordonata;
(iii) dimensiunea timpului pe graficele de timp, pe abscisa etc.
3.4.2 Cateva conexiuni si corelatii descriptive obligatorii
Sa vedem mai intai Plansa I, recapitulativa pentru ceea ce am studiat in aceasta parte.
Plansa I
SINTEZA
studiului economiei cu ajutorul graficelor rectangulare
|
Nr. Ordine |
BAZA DESCRIPTIVA |
DETALII |
COMENTARIU |
||
I |
Felul reflectarii |
curbe |
individuale |
|
|
|
|
multiple |
||||
|
reflectare |
directa |
se cere concretizare (inaplicabila graficului abstract) |
|||
|
indirecta |
|
||||
|
matematic |
functii |
||||
|
nonfunctii (x) |
|
||||
|
II |
Forma |
dreapta |
|
|
|
|
|
non-dreapta |
tipica |
functii elementare |
||
|
atipica |
monotone |
||||
|
III |
Forma + panta |
crescatoare |
|||
|
|
descrescatoare |
||||
|
mixta |
ne-monotone |
||||
|
IV |
Puncte importante |
intersectii |
cu axele |
|
|
|
|
inter-functii |
||||
|
non-intersectii |
asimptote |
||||
|
puncte extrem |
minim-maxim |
||||
|
puncte inflexiune |
numai pentru curbe mixte |
||||
Dupa care putem insfarsit redacta conexiunile simple si obligatorii, sub forma unui indreptar elementar al studiului.
Plansa II
Indreptar elementar al studiului grafic al economiei
|
(i) |
Curba rectilinie (dreapta): Obligatoriu monotona si prezinta panta constanta Intersecteaza obligatoriu axele, afara de situatia abstragerii intersectiilor: Cu ambele axe - cand functia este descrescatoare in cadranul NE Cu o singura axa - cand functia este crescaroare, perfect elastica sau perfect inelastica in cadranul NE |
|
(ii) |
Curbele (tipic) convexe (cadranul NE): Un domeniu creste in detrimentul celuilalt (curba descrescatoare) Curbe tipice relatiei de substitutie Domeniul care creste prezinta crestere crescanda Domeniul care descreste descreste incetinit Intersectia cu axele este mai putin prezenta si/sau relevanta |
|
(iii) |
Curbele (tipic) concave (cadranul NE): Curba descrescatoare - un domeniu creste in detrimentul celuilalt Curbe tipice relatiei de substitutie Caracteristici opuse curbeilor convexe, de-a lungul curbei, cu exceptia pantei descrescatoare si concretizarilor in substitutii Intersectia obligatorie si relavanta cu axele rectangulare |
|
(iv) |
Curbe ne-monotone (mixte): Deriva exclusiv din functii polinomiale Prezinta intersectii cu Ox, reale sau imaginare, dupa gradul polinomului Prezinta puncte de extrem (minime plus maxime) dupa gradul polinomului minus unu Prezinta puncte de inflexiune dupa gradul polinomului minus doi Regula importanta: un punct de inflexiune se asociaza la doua puncte de extrem si se traseaza pe curba intre cele doua puncte de extrem succesive Astfel, polinomul de gradul doi se redacteaza (parabolic) cu un singur punct de extrem si fara puncte de inflexiune |
Plansa III
Cateva tipuri de grafice exemplificative

![]()
![]()
![]()
![]()
![]()
![]() OyOyOy
OyOyOy
![]() (a)
(b)(c)
(a)
(b)(c)

![]()
![]()

![]()
![]()
![]()
![]()


![]()
![]()
![]()
![]()
![]()
![]()
![]() OOx O OxOOx
OOx O OxOOx
OyOyOy
(d)(e)(f)
OOxOOx O Ox
OyOy Oy
(g) (h) (i)
OOxOOx OOx
Oy OyOy



![]()
![]()
![]()
(j) (k)(l)

![]()
![]()
![]()
![]()
O Ox OOx O Ox
Oy
![]()
![]()
![]()
![]()
(m)
![]()
![]()
![]()
![]()
O Ox
|
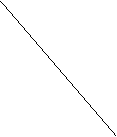
(a) |
Dreapta crescatoare / intersectii cu axele abstrase |
|
(b) |
Dreapta descrescatoare / intersectiile cu axele abstrase |
|
(c) |
Dreapta perfect elastica (orizontala) |
|
(d) |
Dreapta perfect inelastica (verticala) |
|
(e) |
Curba accelerat descrescatoare |
|
(f) |
Curba incetinit crescatoare |
|
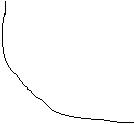
(g) |
Curba ancetinit descrescatoare |
|
(h) |
Curba descrescatoare-crescatoare |
|
(i) |
Curba accelerat crescatoare |
|
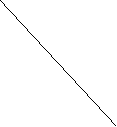
(j) |
Curba atipica, cu evolutie in spirala dreapta, convergenta |
|
(k) |
Camp de curbe tipic convexe (hiperbole) descrescatoare, paralele |
|
(l) |
Curba tipic convexa (hiperbola) descrescatoare, intersectata de doua drepte descrescatoare, dintre care dreapta din stanga formeaza intersectie tangenta cu curba |
|
(m) |
Camp de curbe atipice, rectangulare, dublu paralele cu ambele axe si paralele intre ele |
Concepte:
|
functie |
forma functiei |
|
domeniu de definitie |
panta |
|
domeniul in care functia ia valori (co-domeniu) |
curbele monotone |
|
biunivocitate |
curbele nemonotone |
|
metoda grafica |
convexitate vs. concavitate |
|
non-functie |
|
[1] In redactare matematica:
y (x) = a xn + bx(n-1) + .+ mx + n
[2] Am numit aici, cel putin: convexitatea versus concavitatea si punctele importante.
[3] De observat, astfel, ca maximele si minimele:
(i) nu identifica valori nedepasite de aceeasi functie, atat in partea superioara cat si in cea inferioara;
(ii) valorile maxime si minime se refera exclusiv la dimensiunea de pe ordonata, independent de faptul ca aceasta identifica sau nu domeniul endogen.
[4] Pentru o functie polinomiala de forma:
y = axn + bx(n-1) + .+ mx + n
derivata de ordinul intai este de forma:
y' = na x(n-1) + b(n-1) x(n-2) + .+ jx + m
cu solutii (y'=0) indicand coordonatele (x) - coordonatele (y) vor rezulta din introducerea solutiilor (x) ale lui (y'=0) in expresia (y).
Derivata de ordinul al doilea este de forma:
y'' = an(n-1) x(n-2) + b(n-1)(n-2) x(n-3) + .+ix + j
cu solutii de (x) indicand coordonatele pe abscisa ale punctelor de inflexiune - coordonatele (y) ale acelorasi puncte vor necesita introducerea acelorasi solutii (x) in expresia functiei (y).
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||
|
|||
Analize pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








