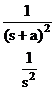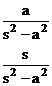| Afaceri | Agricultura | Comunicare | Constructii | Contabilitate | Contracte |
| Economie | Finante | Management | Marketing | Transporturi |
Electrica
|
|
Qdidactic » bani & cariera » constructii » electrica Transformata Laplace |
Transformata Laplace
Transformata Laplace
Se vor rezuma cateva dintre principalele proprietati ale transformatei Laplace, indispensabile rezolvarii catorva aplicatii la acest capitol.
O functie reala f(t), numita functie original, admite transformata Laplace, daca satisface conditiile:
a) este nula in intervalul ![]() ;
;
b) e neteda pe portiuni: marginita, contine cel mult discontinuitati finite si e integrabila in origine;
c)
exista ![]() pentru care:
pentru care:
![]() pentru
pentru ![]()
Imaginea sau transformata Laplace
a acestei functii original este o functie
de variabila complexa ![]() definita astfel:
definita astfel:
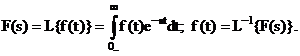 (8.17)
(8.17)
Functia F(s) este
analitica in tot semiplanul ![]()
Cateva proprietati ale transformatei Laplace
a) Liniaritatea deriva din proprietatile integrarii:
![]() (8.18)
(8.18)
b)Transformata derivatei unei functii:
![]() (8.19)
(8.19)
este demonstrabila aplicand integrarea prin parti in relatia (8.17).
c) Transformata Laplace a integralei:
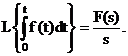 (8.20)
(8.20)
d) Teorema translatiei variabilei complexe (sau a deplasarii):
![]() (8.21)
(8.21)
rezulta din insasi definitia (8.17).
e)Teorema intarzierii (sau a retardarii):
![]() (8.22)
(8.22)
unde
![]() este functia treapta unitate, iar demonstrarea
teoremei decurge din schimbarea de variabila
este functia treapta unitate, iar demonstrarea
teoremei decurge din schimbarea de variabila ![]()
f)Teorema schimbarii scalei (sau a asemanarii):
![]() (8.23)
(8.23)
rezulta direct din definitia (8.17).
Transformate Laplace ale unor functii uzuale
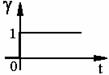 a) Functia treapta unitate este definita
astfel, (fig.8.8):
a) Functia treapta unitate este definita
astfel, (fig.8.8):
![]()
![]() (8.24) Fig. 8.8
(8.24) Fig. 8.8
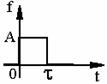
b) Functia impuls dreptunghiular (fig. 8.9) este :
![]()
|
iar din relatiile (8.18), (8.22) si (8.24) rezulta:
Fig. 8.9
![]() (8.25)
(8.25)

c) Functia impuls unitate (Dirac sau delta) poate fi definita la limita ca derivata a functiei treapta unitate:
![]()
Fig. 8.10
Desigur ca functia ![]() nu e derivabila
dar, la limita, in figura 8.10a se poate considera ca saltul are loc
de la 0 la 1 in timpul
nu e derivabila
dar, la limita, in figura 8.10a se poate considera ca saltul are loc
de la 0 la 1 in timpul ![]() . Derivata acestei functii e impulsul dreptunghiular din
figura 8.10b, cu valoarea
. Derivata acestei functii e impulsul dreptunghiular din
figura 8.10b, cu valoarea ![]() , iar
, iar 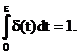
Transformata Laplace a impulsului unitate e data de relatiile (8.19) si (8.24):
![]() (8.26)
(8.26)
d) Functia exponentiala are imaginea:
 (8.27)
(8.27)
iar
in cazul particular ![]() se obtine
relatia (8.24). Alta functie uzuala:
se obtine
relatia (8.24). Alta functie uzuala:
![]() (8.28)
(8.28)
e) Functii trigonometrice. In electrotehnica, marimile sinusoidale apar sub forma canonica, asa ca intereseaza expresia:
![]() (8.29)
(8.29)
dar
cazurile particulare ![]() si
si ![]() dau relatiile:
dau relatiile:
![]()
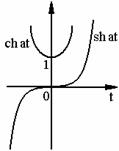
f) Functii hiperbolice. Date fiind definitiile lor:
![]()
transformatele Laplace se afla cu relatiile (8.18) si (8.27):
Fig. 8.11
![]() (8.30)
(8.30)
Utilizarea
transformatei Laplace la studiul regimurilor tranzitorii ale circuitelor
evita (fig. 8.12) rezolvarea dificila a unor sisteme de ecuatii
integro-diferentiale. Datorita 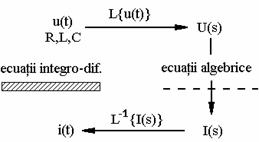 proprietatilor
(8.19) si (8.20), derivatele si integralele unor functii de timp
sunt inlocuite in domeniul s cu inmultiri, respectiv impartiri
cu s.
proprietatilor
(8.19) si (8.20), derivatele si integralele unor functii de timp
sunt inlocuite in domeniul s cu inmultiri, respectiv impartiri
cu s.
Sistemele devin algebrice si sunt mai accesibile. Ramane problema revenirii in domeniul timp, deci aflarea transformatei Laplace inverse a unor functii.
Fig. 8.12
Metode de inversiune. Fiind data transformata Laplace, se cere functia original. Formula Mellin-Fourier:
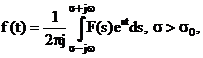
prezinta mai mult interes teoretic.
Practic, aflarea functiei original:
![]()
are la baza teoremele dezvoltarii, ale lui Heaviside. Functia F(s) fiind de obicei un raport de polinoame cu coeficienti reali (desi variabila s este complexa), se poate descompune in fractii simple. Pe urma, o fractie simpla poate avea numitor de gradul I, cand are ca inversa o exponentiala data de relatia 8.27), sau de gradul II, cind numitorul are radacini imaginare si inversa Laplace a functiei e, conform relatiei (8.29), o functie trigonometrica.
Tabel cu principalele transformate Laplace
|
Nr. |
f(t) |
F(s) |
|
Nr. |
f(t) |
F(s) |
|
1 |
|
1 |
4 |
|
|
|
|
2 |
|
|
||||
|
3 |
|
|
5 |
sh at ch at |
|
Sunt utile tabelele cu transformate Laplace, iar pentru a aduce fractia simpla la forma exacta din tabel, sunt necesare deseori proprietatile (8.18)-(8.23).
Exemplu
Se cere inversiunea Laplace:
![]()
Radacinile numitorului fiind complexe, se aduce functia la forma din relatia (8.29), dar numaratorul avand si termen de gradul intai, se face apel la teorema translatiei sau deplasarii (8.21):
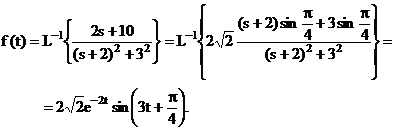
Evident
ca, in expresia fortata la numarator, a si b nu sunt,
in general, sinus respectiv cosinus ale aceluiasi unghi ![]() , decat daca
, decat daca ![]() De aceea, s-a scos in
fata fractiei factorul
De aceea, s-a scos in
fata fractiei factorul ![]()
Graficul
functiei e al unei sinusoide amortizate (fug. 8.13), cu extremele pe
exponentialele ![]() . Se acorda atentie corelarii constantei de
timp
. Se acorda atentie corelarii constantei de
timp ![]() cu perioada sinusoidei
cu perioada sinusoidei
![]() .
.
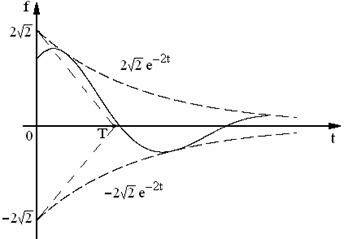
Fig. 8.13
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||||||
|
|||||||
|
|||||||
Documente online pe aceeasi tema | |||||||
|
| |||||||
|
|||||||
|
|
|||||||