
| Afaceri | Agricultura | Comunicare | Constructii | Contabilitate | Contracte |
| Economie | Finante | Management | Marketing | Transporturi |
Electrica
|
|
Qdidactic » bani & cariera » constructii » electrica Legea lui Gauss si aplicatii |
Legea lui Gauss si aplicatii
Legea lui Gauss si aplicatii
Fie o
suprafata infinitezimala ![]() din jurul unui punct P. Sa presupunem ca in
punctul P se suprapun mai multe campuri de intensitati
din jurul unui punct P. Sa presupunem ca in
punctul P se suprapun mai multe campuri de intensitati ![]() . In conformitate cu principiul superpozitiei campurilor
electrice, campul electric rezultant este dat de formula (I.18). Daca
inmultim scalar formula (I.18) cu
. In conformitate cu principiul superpozitiei campurilor
electrice, campul electric rezultant este dat de formula (I.18). Daca
inmultim scalar formula (I.18) cu ![]() , rezulta:
, rezulta:
![]()
cum:
![]()
este fluxul total prin suprafata
![]() iar:
iar:
![]()
este fluxul campului electric ![]() , rezulta:
, rezulta:
![]() (I. 22)
(I. 22)
Relatia de mai sus se numeste legea adunarii fluxurilor electrice.
Sa analizam cu atentie fluxul produs de o sarcina punctiforma printr-o suprafata.
La distanta r de sarcina, campul produs de ea este:
![]()
Printr-o suprafata elementara din jurul unui punct situat la distanta r de sarcina fluxul electric va fi:
![]()

Fig. 24 Fluxul electric produs de o sarcina punctiforma prin suprafata elementara dS
Evident,
![]()
unde dS’ este proiectia
lui dS pe o suprafata sferica de raza r cu
centru in q. Marimea: ![]() se
numeste unghi solid.
se
numeste unghi solid.
Deci:
![]() (I. 23)
(I. 23)
Fluxul electric produs de o sarcina punctiforma printr-o suprafata finita va fi proportional cu unghiul solid sub care se vede suprafata din punctul unde se afla sarcina. Adica:
![]() (I. 24)
(I. 24)
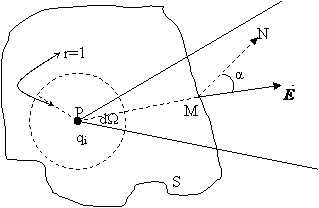
Sa consideram acum cazul in care suprafata este o suprafata inchisa ce inconjoara sarcina.
|
Fig. 25 Suprafata ce inconjoara o sarcina punctiforma
Unghiul solid sub care se vede suprafata din punctul unde se afla sarcina este unghiul total adica 4π. Tinand cont de formula (I.24) rezulta:
![]() (I. 25)
(I. 25)
Daca suprafata este tot o suprafata inchisa dar sarcina este in afara ei se constata ca pentru orice suprafata elementara exista o suprafata elementara complementara ce se vede sub acelasi unghi solid.
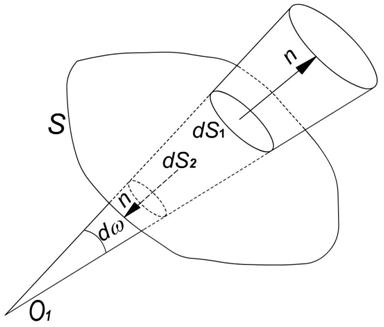
Fig. 26. Suprafata inchisa situata in afara sarcinii punctiforme q
Prin cele doua suprafete elementare fluxurile au aceeasi valoare dar, datorita orientarii diferite a normalelor in raport cu liniile de camp, semne contrarii. Deci:
![]()
Fluxul total va fi totdeauna nul.
In aceste conditii, tinand cont de legea adunarii fluxurilor electrice, rezultatul nostru se poate generaliza la orice distributie de sarcina electrica sub forma:
Fluxul electric printr-o suprafata inchisa este egal cu raportul dintre sarcina electrica din interiorul suprafetei si permitivitatea electrica a vidului.
Aceasta lege, exprimata prin relatia (I.25), se numeste legea lui Gauss sub forma integrala pentru fluxul intensitatii campului electric.
Fie o suprafata oarecare Σ ce inconjoara un domeniu D. Prin aceasta suprafata trece un camp electric generat de sarcini electrice distribuite atat in interiorul cat si in exteriorul domeniului D.

Fig. 27 Referitor la forma locala a legii lui Gauss
In conformitate cu definitia fluxului electric, fluxul electric total prin suprafata Σ este:
![]() (I. 26)
(I. 26)
Vom introduce marimea ![]() prin relatia:
prin relatia:
![]() (I. 27)
(I. 27)
Deoarece produsul
scalar a doi vectori ![]() este:
este: ![]() se poate considera
se poate considera ![]() ca fiind produsul
scalar dintre „vectorul”:
ca fiind produsul
scalar dintre „vectorul”:
![]()
si vectorul ![]() . Acest „vector” se noteaza cu si
se numeste operatorul nabla.
. Acest „vector” se noteaza cu si
se numeste operatorul nabla.
![]()
Produsul scalar dintre operatorul nabla si un vector se numeste divergenta acelui vector.
In conformitate cu teorema lui Gauss-Ostrogradski:
![]() (I. 28)
(I. 28)
Din relatiile: (I.26) si (I.28) rezulta expresia fluxului total din jurul unui domeniu infinitezimal:
![]()
In conformitate cu legea lui Gauss:
![]()
Din comparatia ultimelor doua relatii rezulta:
![]() (I. 29)
(I. 29)
Relatia (I.29) reprezinta forma locala a legii lui Gauss.
Legea lui Gauss fiind dedusa din legea lui Coulomb fara ipoteze suplimentare, este echivalenta cu aceasta. Avantajul legii lui Gauss in comparatie cu legea lui Coulomb apare in cazul campurilor cu simetrie. In cazul in care fluxul electric poate fi calculat usor atunci, folosind legea lui Gauss, se poate deduce intensitatea campului electric. Daca avem campuri electrice ce nu prezinta simetrie legea lui Gauss nu poate fi folosita pentru aflarea intensitatii campului electric. In aceste conditii trebuie sa folosim formula de definitie a intensitatii campului electric - formula care rezulta din legea lui Coulomb si legea superpozitiei campurilor electrice.
Aplicatii
Problema 2. 1.
Sa se gaseasca valoarea intensitatii campului electric intr-un punct oarecare al axei unei spire circulare de raza a situata in vid, incarcata uniform cu densitatea liniara de sarcina electrica λ
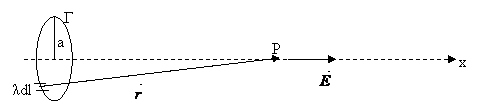
Fig. 28 Referitor la problema 2. 1.
Din motive de simetrie, vectorul intensitate intr-un punct de pe axa Ox nu are componenta decat de-a lungul acestei axe:
![]()
deoarece ![]()
Rezultatul mai poate fi scris sub forma:
![]()
![]() fiind versorul axei Ox.
fiind versorul axei Ox.
Problema 2. 2
Sa se calculeze intensitatea campului electric intr-un punct P situat la distanta x de un plan incarcat uniform cu sarcina electrica cu densitatea superficiala σ
Datorita simetriei plane perfecte, se poate aplica teorema lui Gauss, alegand ca suprafata inchisa pentru calculul fluxului, un paralelipiped, astfel cum se arata in fig. 29. Din motive de simetrie, vectorul intensitate a campului electric este orientat normal pe planul incarcat. In consecinta, fluxul electric prin fetele laterale (perpendiculare pe plan) este nul, iar fluxul prin suprafata Σ se reduce la fluxul prin cele doua suprafete de baza de aria A. Cum aceste suprafete se gasesc la aceeasi distanta de plan, de o parte si de alta a lui, din aceleasi motive de simetrie, vectorii intensitate nu pot avea decat aceeasi valoare pe ambele suprafete, dar orientari antiparalele. Deci:
![]()
iar sarcina din interiorul paralelipipedului:
![]()
prin urmare: ![]()
de unde: ![]()
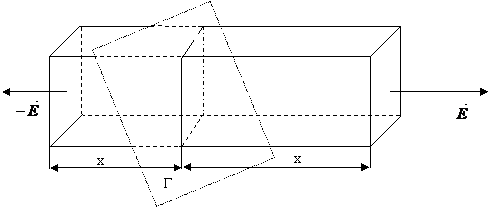
Fig. 29 Referitor la problema 2. 2.
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||||||
|
|||||||
|
|||||||
Referate pe aceeasi tema | |||||||
|
| |||||||
|
|||||||
|
|
|||||||








