
| Afaceri | Agricultura | Comunicare | Constructii | Contabilitate | Contracte |
| Economie | Finante | Management | Marketing | Transporturi |
Arhitectura
|
|
Qdidactic » bani & cariera » constructii » arhitectura Proiectare - formularea problemelor de optimizare. obtinerea modelui matematic. |
Proiectare - formularea problemelor de optimizare. obtinerea modelui matematic.
PROIECTARE - FORMULAREA PROBLEMELOR DE OPTIMIZARE. OBTINEREA MODELUI MATEMATIC.
Asa cum am aratat, problemele de optimizare acopera in mod firesc mai multe domenii. Astfel in constructii proiectantii trebuie sa aleaga materiale si dimensiuni pentru elementele utilizate asa incit sa obtina o structura sigura dar si o solutie cit mai economica. Un manager de portofoliu dintr-un fond mutual de investitii, trebuie sa aleaga acele plasamente care sa produca cele mai bune beneficii pentru investitori dar sa si minimizeze riscurile investitiilor. Pentru un manager de capacitate de productie, cerintele sunt sa dimensioneze fluxurile productive in limita resurselor financiare disponibile atit pentru a satisface cerintele de uzinare ale clientilor dar si pentru a maximiza profitul unitatii. Iar un cercetator este interesat sa obtina o functie matematica care descrie cit mai bine realitateafizica pe baza masuratorilor efectuate. Toate aceste probleme aparent foarte diverse au in comun trei lucruri:
-pentru fiecare activitate exista un anume obiectiv
-alaturi de obiectivul propus, fiecare problema are de obicei si un set de cerinte, restrictii care trebuiesc respectate
-in toate aceste situatii exista obiective si alternative. Alternativele reprezinta variabilele de optimizare. Acele variabile care nu afecteaza obiectivul sunt evident excluse.
Pentru formularea problemei de optimizare se parcurg mai multe etape
-se selecteaza una sau mai multe variabile de optimizare (variabile de design)
-se alege functia obiectiv
-se identifica setul de constringeri
Functia obiectiv cit si setul de constringeri sunt functii matematice exprimate in raport cu una sau mai multe variabile de optimizare. Modelul matematic astfel obtinut urmeaza sa fie rezolvat prin diverse tehnici adaptate la natura ecuatiilor care sunt folosite. Dupa cum se poate observa, etapa de determinare a modelului matematic este extrem de importanta deoarece ea implica o dubla competenta: specialistul trebuie sa cunoasca foarte bine fenomenul ce urmeaza a fi optimizat pentru a selecta variabilele de optimizare cu adevarat semnificative, intregul set de restrictii, expresiile corecte pentru funtia obiectiv ori pentri restrctii dar trebuie in acelasi timp sa stapineasca si tehnicile de optimizare care urmeaza a fi aplicate, alegind-o pe aceea care poate rezolva problema cu cele mai bune rezultate.
Deoarece din punctul de vedere ingineresc, formularea modelului matematic este esentiala, vom prezenta mai multe tipuri de probleme de optimizare pentru care vom dezvolta modelele matematice specifice. La acest nivel nu neintereseza inca sa clasificam aceste modele pentru a aplica metodele specifice de rezolvare.
EXEMPLUL 1.
Pentru a economisi
energia necesara climatizarii unei cladiri (incalzire si
aer conditionat) un proiectant considera o solutie de tip
rectangulara partial ingropata. Spatiul total al unui etaj este
de 20.000 ![]() . Dimesiunea fiecarui spatiu tipizat interior
limiteaza planul constructiei la 50m. S-a decis ca in
constructie sa se foloseasca ’’proportia de aur adica 1.618 si a reyultat ca
tnaltimea incaperilor este de 3.5m. Costurile de
climatizare sunt estimate la 100
. Dimesiunea fiecarui spatiu tipizat interior
limiteaza planul constructiei la 50m. S-a decis ca in
constructie sa se foloseasca ’’proportia de aur adica 1.618 si a reyultat ca
tnaltimea incaperilor este de 3.5m. Costurile de
climatizare sunt estimate la 100 ![]() pentru suprafata
expusa a cladirii. Proprietarul cladirii a cerut ca pretul total
anual al energiei pentru climatizare sa fie mai mic de 225.000 $. Formulati
problema de optimizare asa incit sa se obtina costuri de
excavatie minime.
pentru suprafata
expusa a cladirii. Proprietarul cladirii a cerut ca pretul total
anual al energiei pentru climatizare sa fie mai mic de 225.000 $. Formulati
problema de optimizare asa incit sa se obtina costuri de
excavatie minime.
Pentru rezolvare vom considera figura urmatoare:
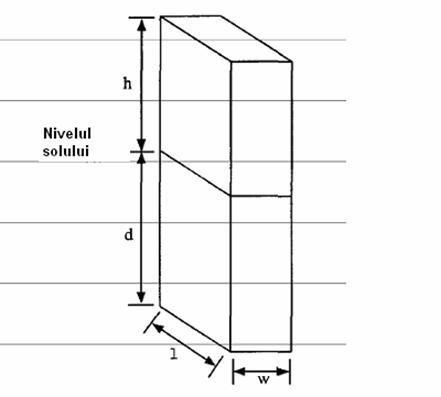
unde s-au notat:
n=numarul de spatii interioare standard![]()
d=adincimea cladirii plasata subteran
h=inaltimea cladirii de la suprafata pamintului
l=lungimea cladirii in plan
w=latimea cladirii in plan
Functia obiectiv isi propune sa minimizeze costurile de excavatie. Acceptind faptul ca aceste costuri sunt proportionale cu volumul excavat, rezulta funtia obiectiv exprimata prin:
Min ![]()
Constringerile provin din faptul ca variabilele nu sunt independente, asa cum rezulta din textul problemei. Astfel este data inaltimea fiecarui etaj, numarul de spatii standard si inaltimea totala a cladirii sunt interconectate prin:
![]()
![]()
De asemenea proportia de aur folosita intervine prin:
![]()
Spatiul total al fiecarui etaj este legat de spatiul stadard tipizat al fiecarei unitati:
![]()
Apoi lotul disponibil aduce limitele sale:
![]()
![]()
Costul total al energiei consumate pentru climatizare este proportional cu aria expusa a cladirii si trebuie sa se inscrie in suma impusa de beneficiar:
![]()
Din punct de vedere fizic, se impun si urmatoarele constringeri:
l, w, h, d![]() si
si
n![]() trebuie sa fie
un numar intreg
trebuie sa fie
un numar intreg
Problema completa de optimizare se enunta in aceste conditii astfel:
Sa se determine setul de marimi (n, l, w, h, d) care sa relalizeze:
Min dlw
considerind restrictiile:
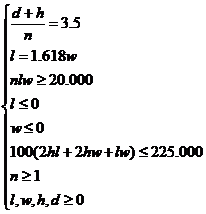
EXEMPLUL 2.
O fabrica de anvelope poate produce doua tipuri de anvelope pentru masini: radiale si inclinate. Pe durata verii fabrica a contractat urmatoarele comenzi:
|
Data |
Tip radial |
Tip inclinat |
|
30 iunie |
|
|
|
31 iulie |
|
|
|
31 august |
|
|
|
Total |
|
|
Fabrica are doua tipuri de masini de productie, A si B, care au matrite apropiate de producere a anvelopelor. Productiile lor orare pe durata verii sunt:
Productivitatea masinilor in termeni de anvelope/ora este:
|
Tip |
Masina A |
Masina B |
|
Radial |
|
|
|
inclinat |
|
|
Costurile de productie sunt de 10$ pentru ora de operare, indiferent de tipul masinii ori de tipul pneului.
Costurile materialelor sunt de 5.25$ pentru pneurile radiale si de 4.15$ pentru cele inclinate.
Finisarile, impachetatul si transportul costa 0.4$ pentru o anvelopa.
Excesul de anvelope este raportat pentru luna urmatoare dar aduce cheltuieli suplimentare de 0.15$ pentru fioecare anvelopa.
Pretul a fost negociat la 20$ pentru anvelopele radiale si 15$ pentru cele inclinate.
Cum trebuie programata productia asa incit sa fie onorate contractele dar sa si maximizeze profitul fabricii
Variabilele de optimizare sunt:
![]() nr de anvelope radiale produse in iunie de masina A
nr de anvelope radiale produse in iunie de masina A
![]() nr de anvelope radiale produse in iulie de masina A
nr de anvelope radiale produse in iulie de masina A
![]() nr de anvelope radiale produse in august de masina A
nr de anvelope radiale produse in august de masina A
![]() nr de anvelope inclinate produse in iunie de masina A
nr de anvelope inclinate produse in iunie de masina A
![]() nr de anvelope inclinate produse in iulie de masina A
nr de anvelope inclinate produse in iulie de masina A
![]() nr de anvelope inclinate produse in august de masina A
nr de anvelope inclinate produse in august de masina A
![]() nr de anvelope radiale produse in iunie de masina B
nr de anvelope radiale produse in iunie de masina B
![]() nr de anvelope radiale produse in iulie de masina B
nr de anvelope radiale produse in iulie de masina B
![]() nr de anvelope radiale produse in august de masina B
nr de anvelope radiale produse in august de masina B
![]() nr de anvelope inclinate produse in iunie de masina B
nr de anvelope inclinate produse in iunie de masina B
![]() nr de anvelope inclinate produse in iulie de masina B
nr de anvelope inclinate produse in iulie de masina B
![]() nr de anvelope inclinate produse in august de masina B
nr de anvelope inclinate produse in august de masina B
Functia obiectiv:
Obiectivul problemei este sa se maximizeze profitul companiei. Profitul este obsinul scazind din veniturile totale obtinute din vinzari, costurile totale de productie, depozitare si transport:
Veniturile din vinzari sunt:
![]()
Costurile materiilor sunt:
![]()
Coasturile de productie sunt:
![]()
Finisarile, impachetatul si tranportul au costurile:
![]()
Excesul de productie produce cheltuieli mai dificil de formulat matematic, asa ca propunem pentru inceput situatia in care nu se produce exces la finalul lunilor de vara.
Excesul de productie la final de iunie este:
![]()
Excesul de productie la final de iulie este:
![]()
Adunind toate costurile si scazindu’le din venituri, se obtine funtia de maximizat
Max ![]() Constringerile sunt date de livrarile lunare din
contract si din asumarea faptului ca la finalul lunilor de vara
firma nu va avea productie in exces:
Constringerile sunt date de livrarile lunare din
contract si din asumarea faptului ca la finalul lunilor de vara
firma nu va avea productie in exces:
![]()
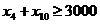
![]()
![]()
![]()
![]()
Productia orara a masinilor este limitata. Pe baza ei apar urmatoarele restrictii:
![]()
![]()
![]()
![]()
![]()
![]()
De asemenea se presupune ca toate variabilele enuntate sunt pozitive.
Problema se scrie acum ca problema de optimizare sub forma:
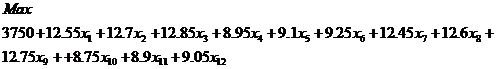
Considerind restrictiile:
![]()
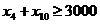
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
EXEMPLUL 3.
Un fond de investitii trebuie sa decida ce procentaj din capitalul total va investi diverse actiuni. Cerintele participantilor la fond este sa aibe un profit anual de minim 10% dar sa se si minimizeze riscurile pierderilor majore. In ultimii 6 ani, ratle profiturilor din diverse tipuri de investitii sunt:
|
Tip investitie |
Rata profit |
Rata profit |
Rata profit |
Rata profit |
Rata profit |
Rata profit |
Valori medii |
|
anul |
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
imobiliar |
|
|
|
|
|
|
|
|
Bonuri tezaur |
|
|
|
|
|
|
|
Astfel variabilele de optimizat sunt:
|
|
Partea de capital investita in actiuni tipA |
|
|
Partea de capital investita in actiuni tipB |
|
|
Partea de capital investita in imobiliar |
|
|
Partea de capital investita in bonuri de tezaur |
Functia obiectiv: trebuie sa minimizeze riscul pierderilor. Acest rist este datorat fluctuatiilor din ratele de profit a investitiilor. O masura a riscului investitional se calculeaza prin suma fluctuatiilor din ratele de profit din valoarea lor medie. Varianta investitiei j se defineste astfel:
![]()
unde:
n![]() numarul total de observatii
numarul total de observatii
![]() rata profitului pentru investitia j la a k-a observatie
(de exemplu un an)
rata profitului pentru investitia j la a k-a observatie
(de exemplu un an)
![]() valoarea media a investitiei j
valoarea media a investitiei j
Pe baza datelor din enuntul problemei, varianta se calculeaza astfel:
![]()
Similar:
![]()
![]()
![]()
Din modul de definire este clar ca varianta evalueaza riscul din cadrul unui tip de investitie. Pentru a estima riscul pentru mai multe tipuri de investitii se foloseste covarianta. Pentru doua tipuri de investitii covarianta se defineste astfel:
![]()
Folosind datele numerice ale problei se calculeaza covariantele:
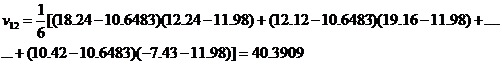
Similar se calculeaza celelalte covariante ![]()
Toate variantele si covariantele calculate se scriu ca matricea variantelor, de tipul:
V
![]()

Riscul investitiilor se exprima pe baza matricei variantei:
![]()

![]()
![]() xT V x
xT V x
Pe baza definitiei roiscului se obtine expresia sa explicita, care reprezinta tocmai functia ce trebuie minimizata:
Min f’![]() 29,0552
29,0552![]() 80,7818
80,7818![]() 0,575767
0,575767![]() -3,90639
-3,90639![]() +267,344
+267,344![]() +
+
+0,375933![]() +0,15971
+0,15971![]() +13,6673
+13,6673![]() -7,39403
-7,39403![]() -0,113267
-0,113267![]()
Restrictiile sunt:
-pentru ca ![]() reprezinta
partt din capitalul total investit, rezulta constringerea:
reprezinta
partt din capitalul total investit, rezulta constringerea:
![]()
-a doua constringere este limita profitului anual stabilita de investitorii fondului
![]()
-toate variabilele sunt pozitive:
![]()
Enuntul complet al problemeii de optimizare este:
sa se determine ![]() asa incit sa
se minimizeze expresia :
asa incit sa
se minimizeze expresia :
Min f’![]() 29,0552
29,0552![]() 80,7818
80,7818![]() 0,575767
0,575767![]() -3,90639
-3,90639![]() +267,344
+267,344![]() +
+
+0,375933![]() +0,15971
+0,15971![]() +13,6673
+13,6673![]() -7,39403
-7,39403![]() -0,113267
-0,113267![]()
in conditiile:
![]()
![]()
![]()
EXEMPLUL 4.
Determinarea celei mai bune expresii care estimeaza un set de date optinute experimental, poate fi formulata ca o problema tipica de optimizare. Se considera astfel datele masurate (variabila z) in funtie de variabilele x si z:
|
Nr crt |
x |
y |
Z (masurata) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tipul si forma functiei se alege la inceput, pe baza experientei cercetatorului si a specificului fenomenului masurat. In acest caz acceptam forma generala urmatoare:
![]()
Obiectivul este sa determinam cele mai bune valori pentru
coeficientii ![]() care sa
minimizeze suma erorilor intre valorile masurate si cele calculate pe baza
formulei.
care sa
minimizeze suma erorilor intre valorile masurate si cele calculate pe baza
formulei.
Variabilele de optimizare sunt ![]()
Functia obiectiv este:
![]()
Folosind datele numerice ale problemei se obtine expresia functei obiectiv:
![]()
Dupa calcule expresia devine:
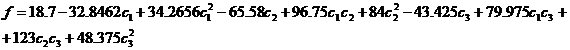
Minimizarea functei determinate este problema de optimizare. Se
observa ca in acest caz nu exista restrictii impuse variabilelor
![]() .
.
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
||||||||||
|
||||||||||
|
||||||||||
Proiecte pe aceeasi tema
| ||||||||||
|
| ||||||||||
|
||||||||||
|
|
||||||||||








