
| Aeronautica | Comunicatii | Drept | Informatica | Nutritie | Sociologie |
| Tehnica mecanica |
Informatica
|
|
Qdidactic » stiinta & tehnica » informatica Sisteme numerice 1d si 2d - lucrarea de laborator |
Sisteme numerice 1d si 2d - lucrarea de laborator
sisteme numerice 1D Si 2D - lucrarea de laborator
Obiectivele lucrarii
1) Asimilarea functiilor MATLAB specifice lucrului cu sisteme discrete 1D si 2D;
2 Studiul proprietatilor de liniaritate, invarianta in timp si stabilitate, in cazul sistemelor numerice
3) Deprinderea tehnicilor de determinare a functiei pondere, functiei indiciale, precum si raspunsului sistemelor numerice la diverse secvente discrete;
4) Studiul interactiv al proprietatilor secventelor discrete si al operatorilor aplicati acestora utilizand mediul DIDACTICIEL.
Desfasurarea lucrarii
Sisteme numerice liniare 1D
Sa se verifice ca sistemul numeric reprezentat prin functia de transfer:

este un sistem liniar si invariant in timp.
1)
clear; n = 0:40; a = 2; b = -3;
x1 = cos(2*pi*0.1*n); x2 = cos(2*pi*0.4*n);
x = a*x1 + b*x2;
num = [2.2403 2.4908 2.2403]; den = [1 -0.4 0.75]; ic = [0 0];
y1 = filter(num, den, x1, ic); y2 = filter(num, den, x2, ic);
y = filter(num, den, x, ic); yt = a*y1 + b*y2; d = y - yt;
figure
subplot(3, 1, 1); stem(n, y); ylabel('Amplitudine');
title('Iesirea pt intrarea ponderata: a cdot x_[n] + b cdot x_[n]');
subplot(3, 1, 2); stem(n, yt); ylabel('Amplitudine');
title('Iesire: a cdot y_[n] + b cdot y_[n]');
subplot(3, 1, 3); stem(n, d);
xlabel('Index temporal n'); ylabel('Amplitudine');
title(' Semnal diferenta');
2)
clear; n = 0:40; D = 10; a = 3.0; b = -2;
x = a*cos(2*pi*0.1*n) + b*cos(2*pi*0.4*n); xd = [zeros(1, D) x];
num = [2.2403 2.4908 2.2403]; den = [1 -0.4 0.75]; ic = [0 0];
y = filter(num, den, x, ic); yd = filter(num, den, xd, ic);
d = y - yd(1+D:41+D);
figure
subplot(3, 1, 1); stem(n, y); ylabel('Amplitudine');
title('Iesire y[n]'); grid;
subplot(3, 1, 2); stem(n, yd(1:41)); ylabel('Amplitudine'); grid;
title(['Iesire pt intrarea decalata x[n -', num2str(D), ']']);
subplot(3, 1, 3); stem(n, d);
xlabel('Index temporal n'); ylabel('Amplitudine');
title(' Semnal diferenta'); grid;
Functia de transfer, polii si zerourile unui sistem numeric
Fie un ![]() caracterizat in
domeniul timp discret de ecuatia:
caracterizat in
domeniul timp discret de ecuatia:
![]()
Sa se determine functia de transfer, polii si zerourile acestui sistem.
Functia de transfer corespunzatoare este data de:
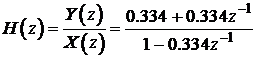
clear; b=[0.334, 0.334]; a=[1.0, -0.334];
figure(1) ; zplane(b, a) ;
figure(2) ; freqz(b, a)
Functia pondere a unui sistem numeric
1)
Sa se determine functia pondere pentru un ![]() definit prin
functia de transfer:
definit prin
functia de transfer:
|

2) Sa se compare functiile pondere pentru doua FTB de tip Butterworth si Cauer de ordinul 5, avand frecventa de taiere normata de 0.5.
1)
clear; N = 40;
num=[2.2403 2.4908 2.2403];
den= [1 -0.4 0.75];
y = impz(num, den, N); figure
stem(y); xlabel('Index temporal n');
ylabel('Amplitudine'); title('Functia pondere'); grid;
2)
clear; [b, a]=butter(5, 0.5); h=impz(b, a, 50);
figure; subplot(211); stem(h); title('butterworth ')
[b, a]=ellip(5, 1, 20, 0.5); h=impz(b, a, 50);
subplot(212); stem(h); title('cauer ')
Stabilitatea sistemelor numerice
Sa se arate ca sistemul numeric caracterizat prin functia de transfer:

este stabil.
clear; num = [1 -0.8]; den = [1 1.5 0.9];
N = 200; h = impz(num, den, N+1); parsum = 0;
for k = 1:N+1;
parsum = parsum + abs(h(k));
if abs(h(k)) < 10^(-6),
break,
end
end
figure
n = 0:N; stem(n, h)
xlabel('Index temporal n'); ylabel('Amplitudine');
figure
zplane(num, den); disp('Sum ='); disp(abs(h(k)));
Conectarea in cascada a sistemelor numerice
Fie doua sisteme numerice definite prin functiile de transfer urmatoare:
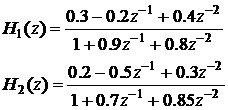
Aratati ca functia de transfer a sistemului numeric obtinut prin conectarea in cascada a celor doua sisteme este egala cu produsul functiilor de transfer ale acestora.
clear; x = [1 zeros(1, 40)]; n = 0:40;
den = [1 1.6 2.28 1.325 0.68]; num = [0.06 -0.19 0.27 -0.26 0.12];
y = filter(num, den, x);
num1 = [0.3 -0.2 0.4]; den1 = [1 0.9 0.8];
num2 = [0.2 -0.5 0.3]; den2 = [1 0.7 0.85];
y1=filter(num1, den1, x); y2=filter(num2, den2, y1); d=y-y2;
figure; subplot(3, 1, 1); stem(n, y); ylabel('Amplitudine');
title('Iesirea sistemului rezultat'); grid;
subplot(3, 1, 2); stem(n, y2); ylabel('Amplitudine');
title('Iesirea celor doua sisteme conectate in cascada'); grid;
subplot(3, 1, 3); stem(n, d)
xlabel('Index temporal n'); ylabel('Amplitudine');
title(' Semnal diferenta'); grid;
Functia indiciala a unui sistem numeric
Sa se compare functiile indiciale pentru doua FTB de tip Butterworth si Cauer de ordinul 5, avand frecventa de taiere normata de 0.5.
clear; [b, a]=butter(5, 0.5);
unit=[ones(50, 1)]; h=filter(b, a, unit);
subplot(211); stem(h); title('butterworth')
[b, a]=ellip(5, 1, 20, 0.5); h=filter(b, a, unit);
subplot(212); stem(h); title('cauer')
Efectul zerourilor si polilor asupra functiei de transfer a unui sistem numeric
1) Fie
sistemul reprezentat prin functia de transfer ![]() prezentand
un singur zerou la
prezentand
un singur zerou la ![]() . Sa se studieze variatia lui
. Sa se studieze variatia lui ![]() la apropierea zeroului
de cercul unitate.
la apropierea zeroului
de cercul unitate.
2)
Procedati in acelasi mod pentru sistemul
reprezentat prin functia de
transfer  , care are
un singur pol la
, care are
un singur pol la ![]() .
.
b(1, 1:2)=[1 -0.4]; b(2, 1:2)=[1 -0.6];
b(3, 1:2)=[1 -0.8]; b(4, 1:2)=[1 -1];
figure; hold on; tipcul=['b'; 'r'; 'g'; 'k'];
for k=1:4
h=freqz(b(k, :), 1); plot(abs(h), tipcul(k, :))
end
axis([0 512 0 2.2]); grid on
legend('zerou=.4', 'zerou=.6', 'zerou=.8', 'zerou=1', 2)
title('Influenta zerourilor asupra functiei de transfer')
a(1, 1:2)=[1 -0.5]; a(2, 1:2)=[1 -0.6];
a(3, 1:2)=[1 -0.7]; a(4, 1:2)=[1 -0.8];
figure; hold on
for k=1:4
h=freqz(1, a(k, :)); plot(abs(h), tipcul(k, :))
end
axis([0 512 0 5.5]); grid on
legend('pol=.5', 'pol=.6', 'pol=.7', 'pol=.8')
title('Influenta polilor asupra functiei de transfer')
Sisteme numerice liniare 2D
Functia
de transfer a unui ![]() de tip nerecursiv
este de forma:
de tip nerecursiv
este de forma:
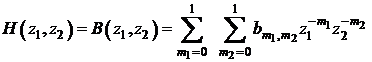
Sa
se determine functia pondere, functia indiciala si
raspunsul la o exponentiala complexa pentru un ![]() avand matricea
coeficientilor:
avand matricea
coeficientilor:
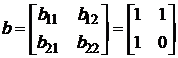
clear; b=[1, 1; 1, 0];
dirac2D=zeros(50); dirac2D(1, 1)=1; h=conv2(b, dirac2D);
subplot(221); mesh(dirac2D); title('impuls Dirac 2D ');
subplot(223); mesh(h); title('functia pondere ')
subplot(222); unit2D=ones(50); mesh(unit2D);
title('functia treapta unitate 2D ');
subplot(224); g=conv2(b, unit2D); mesh(g);
title('functia indiciala ')
for n1=1:64
for n2=1:64
e(n1, n2)=exp(j*n1*2*pi/64)*exp(j*n2*2*pi/64);
end
end
y=conv2(b, e);
figure; subplot(211); mesh(real(e)); rotate3d
title('partea reala a unei exponentiale complexe 2D ')
subplot(212); mesh(real(y)); rotate3d
title('partea reala a raspunsului sistemului ')
Sisteme numerice neliniare 2D
Sa se filtreze imaginea eight.tif", afectata de un zgomot de tip sare si piper de dispersie 0.02, folosind filtre de ordine corespunzatoare statisticilor 1, 4, 5 si 9 si o fereastra de filtrare de 3 3.
Inlocuiti filtrul de ordine corespunzator statisticii 5 cu un filtru median. Ce observati
clear; I = imread('eight.tif');
J = imnoise(I, 'salt & pepper', 0.02);
K1 = ordfilt2(J, 5, ones(3, 3));
K2 = ordfilt2(J, 1, ones(3, 3));
K3 = ordfilt2(J, 9, ones(3, 3));
K4 = ordfilt2(J, 4, [0 1 0; 1 0 1; 0 1 0]);
figure
subplot(321); imshow(I); title('Imagine initiala')
subplot(322); imshow(J); title('Imagine perturbata')
subplot(323); imshow(K1);
title('Filtrare de ordine (statistica 5 - median)')
subplot(324); imshow(K2);
title('Filtrare de ordine (statistica 1 - min)')
subplot(325); imshow(K3);
title('Filtrare de ordine (statistica 9 - max)')
subplot(326); imshow(K4);
title('Filtrare de ordine (statistica 4)')
K = medfilt2(J); figure
subplot(211); imshow(J); title('Imagine initiala')
subplot(212); imshow(K); title('Imagine filtrata')
Studiul sistemelor numerice utilizand mediul DIDACTICIEL
1) Se lanseaza DIDACTICIEL-ul prin introducerea comenzii:
didact
2) Se studiaza interactiv stabilitatea si influenta zerourilor si polilor asupra caracteristicii de transfer a unui SN cu ajutorul meniurilor definite in:
Filtering
Tema
Se dau
functiile de transfer urmatoare, care corespund unor ![]() :
:
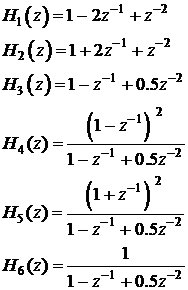
a)
Utilizand functia zplane.m reprezentati in planul Z diagramele
pol-zerourilor pentru functiile ![]() .
.
b) Utilizand functia freqz.m reprezentati caracteristicile de frecventa ale acestor functii de transfer. Precizati ce tip de sisteme reprezinta fiecare.
c)
Determinati raspunsul sistemului ![]() la semnalul impuls
unitate si treapta unitate.
la semnalul impuls
unitate si treapta unitate.
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
||||||||||||||||||||||||
|
||||||||||||||||||||||||
|
||||||||||||||||||||||||
Referate pe aceeasi tema | ||||||||||||||||||||||||
|
| ||||||||||||||||||||||||
|
||||||||||||||||||||||||
|
|
||||||||||||||||||||||||








