
| Aeronautica | Comunicatii | Drept | Informatica | Nutritie | Sociologie |
| Tehnica mecanica |
Informatica
|
|
Qdidactic » stiinta & tehnica » informatica Refacerea semnalelor esantionate |
Refacerea semnalelor esantionate
Refacerea semnalelor esantionate
In general, componentele sistemelor de conducere sunt actionate de semnale continue. In consecinta, intre componentele numerice si cele anologice se introduce un dispozitiv de refacere a datelor. Cel mai obisnuit circuit de refacere a semnalelor analogice este dispozitivul de retinere.
Fie un dispozitiv de
esantionare ideal care esantioneaza cu o pulsatie ![]() , a carui caracteristica spectru
frecventa este cea din Figura
20. Din figura se vede ca semnalul terbuie
filtrate cu un filtru trece-jos ideal ca cel din Figura 21.
, a carui caracteristica spectru
frecventa este cea din Figura
20. Din figura se vede ca semnalul terbuie
filtrate cu un filtru trece-jos ideal ca cel din Figura 21.
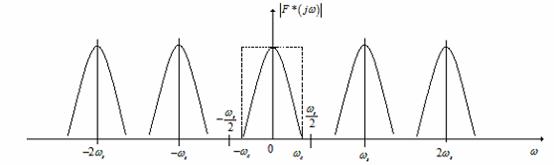
Figura 20 . Refacerea semnalelor analogice cu un filtru trece-jos.
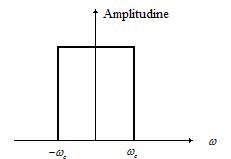
Figura 21 . Caracteristica amplitudine a unui filtru ideal.
Un filtru trece-jos ideal nu este fizic realizabil. Chiar daca s-ar putea realiza un asemenea filtru, presupunerea ca semnalul continuu este de banda limitata nu este totdeauna indeplinita. Pentru aplicatiile practice este deci imposibila o refacere exacta a semnalului continuu dupa ce a fost esantionat. Refacerea semnalului esantionat se face prin aproximarea functiei de timp originale.
La refacerea semnalului avem esantioanele f(0), f(T), ., f(kT). O metoda ce se poate utiliza pentru refacerea valorilor semnalului intre momentele de esantionare, kT si (k+1)T este aceea a dezvoltarii in serie. Fie
fk(t) = f(t) pentru kT <= t < (k+1)T
![]()
Pentru a evalua derivate din formula de mai sus avem disponibile doar valorile functiei f(t) in momentele de esantionare. Este posibil sa estimam derivatele prin diferente finite, de exemplu derivate de ordin intai
|
![]()
Deoarece aproximarea derivatelor de ordin superior duce la circuite complexe, de obicei se utilizeaza aproximarea
fk(t) = f(t) pentru kT <= t < (k+1)T
care se numeste extrapolator de ordin zero. El mentine valoarea esantionata pe timpul perioadei de esantionare, pana la urmatorul esantion. Pentru a deduce functia de transfer a extrapolatorului de ordin zero vom considera raspunsul sau la impuls din
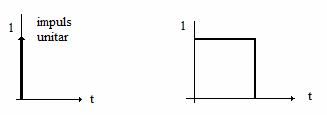
Figura 22. Impuls unitar si raspunsul la impuls unitar al extrapolatorului de ordin zero.
Notam cu 1(t) functia treapta unitara, si raspunsul la impuls al extrapolatorului este
y(t) = 1(t) - 1(t-T)
Functia de transfer a extrapolatorului de ordin zero va fi
![]()
Intrarea intr-un element de extrapolare este cel din Figura 23
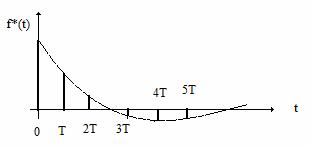
Figura 23 . Semnalul de intrare in extrapolator.
Iesirea extrapolatorului este cea din Figura 24.
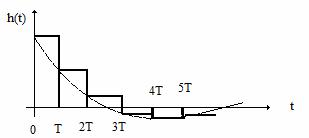
Figura 24 . Iesirea extrapolatorului.
Pentru a determina
caracteristicile de amplitudine si faza ale ale extrapolatorului, vom
inlocui in functia sa de transfer H0(s) pe s cu ![]() si obtinem
si obtinem
![]()
care se poate rescrie
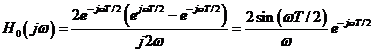
sau
![]()
Deoarece perioada de esantionare T este
![]()
putem scrie
![]()
Modulul lui H0(s) este

iar caracteristica amplitudine a extrapolatorului este cea din Figura 25.
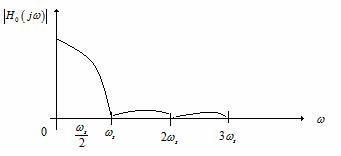
Figura 25 . Caracteristica amplitudine a extrapolatorului de ordin zero
Caracteristica de faza din Figura 26.

Figura 26 . Caracteristica de faza a extrapolatorului de ordin zero.
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2026 - Toate drepturile rezervate -| |
|
|
||||||||||||||||||||||||
|
||||||||||||||||||||||||
|
||||||||||||||||||||||||
Referate pe aceeasi tema | ||||||||||||||||||||||||
|
| ||||||||||||||||||||||||
|
||||||||||||||||||||||||
|
|
||||||||||||||||||||||||








