
| Aeronautica | Comunicatii | Drept | Informatica | Nutritie | Sociologie |
| Tehnica mecanica |
Informatica
|
|
Qdidactic » stiinta & tehnica » informatica Procesul de esantionare ideala |
Procesul de esantionare ideala
Procesul de esantionare ideala
Fie f(t) o functie de timp ce este esantionata cu un esantionator ideal. Fie T perioada de esantionare. Iesirea esantionatorului ideal, f*(t), este un tren de impulsuri cu amplitudinea egala cu cea a semnalului de intrare la momentele de esantionare. Notam cu
![]()
un tren de impulsuri unitare, unde
![]()
Esantionatorul ideal este un contact care se inchide la fiecare T secunde pentru o durata de timp 0. Iesirea esantionatorului ideal este
![]()
unde esantionarea a
inceput la momentul t = 0. Transformata Laplace a functiei ![]() este 1, iar
Tansformata Laplace a functiei
este 1, iar
Tansformata Laplace a functiei ![]() este e-kTs.
Transformata Laplace a functiei f*(t) este
este e-kTs.
Transformata Laplace a functiei f*(t) este
![]()
Semanlele de intrare, trenul de impulsuri unitare si de iesire ale esantionatorului ideal sunt cele din Figura 12, Figura 13 si Figura 14.

Figura 12 . Semnalul de intrare in esantionatorul ideal.
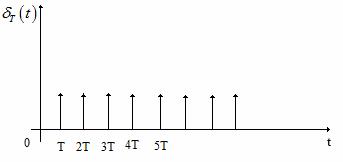
Figura 13 . Trenul de impulsuri unitare.

|
Figura 14 . Semnalul de iesire al esantionatorului ideal.
Fie F(s) transformata
Laplace a functiei f(t) si P(s) transformata Laplace a functiei ![]() .
.
![]()
pentru ![]() .
.
Deoarece f*(t) este produsul a doua functii de timp
![]()
transformata Laplace a functiei f*(t) se poate calcula ca

unde c este abscisa de
convergenta a integralei. Integrala se poate calcula cu teorema reziduurilor.
Pentru aceasta trebuie sa calculam polii functiilor ![]() si
si ![]() .
.
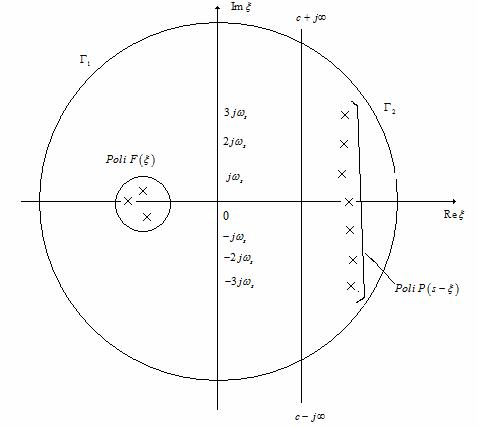
Figura 15 . Integralele de contur pentru calculul functiei F*(s).
Polii functiei ![]() sunt situati in
semiplanul stang. Polii functiei
sunt situati in
semiplanul stang. Polii functiei ![]() sunt simplii, in
numar infinit, si au valorile
sunt simplii, in
numar infinit, si au valorile
![]() ,
, ![]()
unde T este perioada de
esantionare, iar ![]() este pulsatia de
esantionare in rad/s. Distributiile tipice ale acestor poli sunt cele
din Figura 15.
este pulsatia de
esantionare in rad/s. Distributiile tipice ale acestor poli sunt cele
din Figura 15.
Vom calcula integrala
separat pe contururile ![]() si
si ![]() . Daca
. Daca
![]()
atunci integralele pe
semicercurile cu raze infinite din contururile ![]() si
si ![]() dispar. Integrala pe
conturul
dispar. Integrala pe
conturul ![]() se calculeaza
astfel.
se calculeaza
astfel.
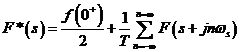
Termenul ![]() are urmatoarea
explicatie. Daca functia f(t) este discontinua,
transformata Laplace inversa are ca rezultat in punctele de
discontinuitate media valorilor laterale ale functiei in acele puncte. In
definitia functiei f*(t), daca functia f(t) este
discontinua in punctele de esantionare, functia f*(t) are ca
valoare limita din dreapta a functiei f(t) ce se esantioneaza.
In formula s-a pus in evidenta termenul
are urmatoarea
explicatie. Daca functia f(t) este discontinua,
transformata Laplace inversa are ca rezultat in punctele de
discontinuitate media valorilor laterale ale functiei in acele puncte. In
definitia functiei f*(t), daca functia f(t) este
discontinua in punctele de esantionare, functia f*(t) are ca
valoare limita din dreapta a functiei f(t) ce se esantioneaza.
In formula s-a pus in evidenta termenul ![]() deoarece sunt cazuri
cand functia f(t) este discontinua in origine.
deoarece sunt cazuri
cand functia f(t) este discontinua in origine.
Integrala pe conturul ![]() se calculeaza
astfel. Fie
se calculeaza
astfel. Fie
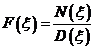
Presupunem pentru simplitate ca polii functiei sunt simpli. Fie
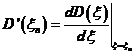
unde ![]() este un pol al
functiei
este un pol al
functiei ![]() , n = 1, 2, ., k.
, n = 1, 2, ., k.

Exemple. Fie functia treapta unitara f(t) = 1(t) esantionata la intervale egale cu T. Iesirea esantionatorului ideal este
![]()
Transformata Laplace a functiei, F*(s) este
![]() , pentru
, pentru ![]()
Sa calculam
F*(s) pe conturul ![]() .
. ![]() deci N(s) = 1, D'(s) =
1, deci
deci N(s) = 1, D'(s) =
1, deci
![]()
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
||||||||||||||||||||||||
|
||||||||||||||||||||||||
|
||||||||||||||||||||||||
Proiecte pe aceeasi tema | ||||||||||||||||||||||||
|
| ||||||||||||||||||||||||
|
||||||||||||||||||||||||
|
|
||||||||||||||||||||||||








