
| Aeronautica | Comunicatii | Drept | Informatica | Nutritie | Sociologie |
| Tehnica mecanica |
Informatica
|
|
Qdidactic » stiinta & tehnica » informatica Prelucrarea multirata a secventelor sau schimbarea ratei de esantionare - lucrarea de laborator |
Prelucrarea multirata a secventelor sau schimbarea ratei de esantionare - lucrarea de laborator
PRELUCRAREA MULTIRATA a SECVENTELOR sau SCHIMBAREA RATEI DE ESANTIONARE - lucrarea de laborator
Obiectivele lucrarii
1) Studiul operatiilor de baza specifice prelucrarii multirata a secventelor numerice;
2) Asimilarea functiilor MATLAB dedicate prelucrarii multirata a secventelor;
3) Studiul unor exemple care sa ilustreze utilizarea prelucrarii multirata in diverse aplicatii ale prelucrarii numerice.
Desfasurarea lucrarii
Comenzi MATLAB pentru prelucrarea multirata
decimate - realizeaza functia
de decimare a unei secvente ![]() cu
cu ![]() , astfel incat
rezulta secventa decimata
, astfel incat
rezulta secventa decimata ![]() cu
cu ![]() .
.
interp - realizeaza functii
de interpolare a unei secvente ![]() cu
cu ![]() , astfelincat
rezulta secventa interpolata
, astfelincat
rezulta secventa interpolata ![]() , cu
, cu ![]()
Decimarea si interpolarea secventelor
Generati cu ajutorul comenzilor MATLAB versiunile decimate si interpolate cu 4 ale unei secvente armonice. Verificati refacerea secventei dupa decimare si interpolare.
Fe=32000; T=1/Fe; t=0:T:1;
x=sin(2*pi*1000*t)+0.3*sin(2*pi*3000*t);
figure(1)
stem(x(1:33)) xlabel('nT, T=31.75 microsec'); grid
xd=decimate(x, 4); figure(2)
stem(xd(1:9)); xlabel('nTd, Td=4T=125 microsec'); grid
xr=interp(xd, 4); figure(3)
stem(xr(1:33)); xlabel('nT, T=31.75 microsec'); grid
Analizati transformatele Fourier ale secventelor: initiala, decimata, interpolata si refacuta.
Interpolatorul de ordinul zero
Un
interpolator de ordinul zero transforma o secventa ![]() aplicata la
intrarea sa repetand fiecare valoare a
secventei de
aplicata la
intrarea sa repetand fiecare valoare a
secventei de ![]() ori, astfel incat functia pondere a unui
astfel de interpolator este:
ori, astfel incat functia pondere a unui
astfel de interpolator este:
![]()
Semnalul
interpolat ![]() se obtine din
relatia
se obtine din
relatia ![]() .
.
Programul
MATLAB de mai jos ilustreaza interpolarea de ordinul zero cu ![]() pentru secventa
pentru secventa ![]() .
.
x=[2 1 0.5 0 0 0 0 0]; xe=expa(x, 3);
h0=[1 1 1 0 0 0 0 0]; y=conv(xe, h0);
subplot(311)
|
stem(x); title('Semnalul x[n]'); grid
subplot(312)
stem(xe); title('Semnalul xe[n]'); grid
subplot(313)
stem(y); title('Semnalul y[n]'); grid
In
secventa de mai sus s-a folosit o functie auxiliara expa.m,
care insereaza intre fiecare
doua esantioane succesive ale secventei ![]() un numar
un numar ![]() de zerouri.
de zerouri.
Iata codul MATLAB al acestei functii:
function xe=expa(x, L)
N=L*length(x); xe=zeros(1, N); xe(1:L:N)=x;
Transmultiplexorul numeric
Transmultiplexorul realizeaza in sens bidirectional legatura dintre formatele de linie numerice si analogice ale sistemelor de multiplexare a canalelor cu diviziune in timp (MDT) si a celor cu diviziune in frecventa (MDF).
In figura 9.1 este prezentat cazul simplu al unui multiplexor cu doua canale.
Semnalul
![]() este, in acest caz, rezultat din conversia A/N a unui semnal de
linie analogic, ce contine
spectrele de frecventa a doua cai multiplexate in
frecventa (vezi fig. 9.1 b)
este, in acest caz, rezultat din conversia A/N a unui semnal de
linie analogic, ce contine
spectrele de frecventa a doua cai multiplexate in
frecventa (vezi fig. 9.1 b)
Semnalele
![]() si
si ![]() sunt secventele
corespunzatoare celor doua cai in format numeric separate din
semnalul
sunt secventele
corespunzatoare celor doua cai in format numeric separate din
semnalul ![]() . Semnalele
. Semnalele ![]() si
si ![]() , pot fi utilizate
separat sau pot fi multiplexate in timp, intr-un format numeric specific echipamentelor
MDT.
, pot fi utilizate
separat sau pot fi multiplexate in timp, intr-un format numeric specific echipamentelor
MDT.
Prelucrarea
numerica a semnalului ![]() pentru obtinerea
semnalelor
pentru obtinerea
semnalelor ![]() si
si ![]() , precum si
prelucrarea lor inversa, pentru
refacerea semnalului
, precum si
prelucrarea lor inversa, pentru
refacerea semnalului ![]() pot fi urmarite
cu usurinta pe schema bloc a transmultiplexorului si pe
spectrele semnalelor notate de la 1 la 8.
pot fi urmarite
cu usurinta pe schema bloc a transmultiplexorului si pe
spectrele semnalelor notate de la 1 la 8.
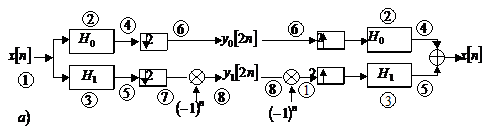

Figura 9.1
Urmatoarea secventa MATLAB simuleaza functionarea acestui transmultiplexor. Pentru simplitatea programului am considerat ca cele doua canale sunt caracterizate de catre o singura sinusoida de frecventa (joasa) de 200 Hz si una (inalta) de 5000Hz.
Fe=16000; t=0:1/Fe:0.01;
x=sin(2*pi*200*t)+sin(2*pi*5000*t);
X=abs(fftshift(fft(x, 512))); vf=((-255:256)/512)*Fe;
figure(1), subplot(211), plot(vf, X),
title('Spectrul semnalului x[n]')
b0=fir2(50, [0 .5 .5 1], [1 1 0 0]);
b1=fir2(50, [0 .5 .5 1], [0 0 1 1]);
[h0, w0]=freqz(b0, 1, 512); [h1, w1]=freqz(b1, 1, 512);
subplot(212), plot(w0/pi, abs(h0), w1/pi, abs(h1)),
title('Spectrele H0 si H1')
x0=filter(b0, 1, x); x1=filter(b1, 1, x);
x0d=x0(1:2:length(x0)); y0=x0d;
x1d=x1(1:2:length(x1));
td=(0:length(x0d)-1)/Fe;
X0=abs(fftshift(fft(x0, 512)));
X1=abs(fftshift(fft(x1, 512)));
figure(2); subplot(211), plot(vf, X0),
title('Spectrul semnalului x0 sau y0')
subplot(212), plot(vf, X1);
title('Spectrul semnalului x1')
vf=((-255:256)/512)*(Fe/2);
X0d=abs(fftshift(fft(x0d, 512)));
X1d=abs(fftshift(fft(x1d, 512)));
figure(3); subplot(211), plot(vf, X0d),
title('Spectrul semnalului x0d')
subplot(212), plot(vf, X1d);
title('Spectrul semnalului x1d')
N2=length(x1d);
for k=0:N2-1
y1(k+1)=((-1)^k)*x1d(k+1);
end
figure(4), subplot(211), plot(td, y1), title('Semnalul y1')
Y1=abs(fftshift(fft(y1, 512)));
subplot(212), plot(vf, Y1), title('Spectrul semnalului y1')
Proiectarea filtrelor de banda ingusta
Sa
proiectam un FTJ cu specificatiile date in figura 9.2 a). Fie ![]() gradul necesar pentru
acest filtru (cu banda de tranzitie
gradul necesar pentru
acest filtru (cu banda de tranzitie ![]() foarte mica!).
foarte mica!).
In
locul proiectarii acestui filtru, care are ![]() , sa
proiectam un FTJ mai simplu, care
are specificatiile prezentate in figura 9.2 b). Evident, in acest caz:
, sa
proiectam un FTJ mai simplu, care
are specificatiile prezentate in figura 9.2 b). Evident, in acest caz: ![]() si, in
consecinta, ordinul filtrului
va fi
si, in
consecinta, ordinul filtrului
va fi ![]() , care inseamna
ca in realizarea sa numarul de multiplicari si de
adunari se va reduce de doua ori. Daca cu
, care inseamna
ca in realizarea sa numarul de multiplicari si de
adunari se va reduce de doua ori. Daca cu ![]() este notata
functia de transfer a acestui filtru, atunci caracteristica de transfer a
functiei
este notata
functia de transfer a acestui filtru, atunci caracteristica de transfer a
functiei ![]() este cea din figura
9.2 c). Insa, acest filtru are
doua benzi de trecere. Prima este cea care intereseaza, iar cea centrata in jurul lui p
este nedorita. Aceasta banda poate fi suprimata cu ajutorul
unui filtru trece jos
este cea din figura
9.2 c). Insa, acest filtru are
doua benzi de trecere. Prima este cea care intereseaza, iar cea centrata in jurul lui p
este nedorita. Aceasta banda poate fi suprimata cu ajutorul
unui filtru trece jos ![]() , foarte simplu, a carui caracteristica de transfer
este ilustrata in figura 9.2 d).
, foarte simplu, a carui caracteristica de transfer
este ilustrata in figura 9.2 d).
Ansamblul
format din filtrele caracterizate de functiile de transfer ![]() si
si ![]() indeplineste
conditiile initial dorite.
indeplineste
conditiile initial dorite.

Figura 9.2
Sa
exemplificam procesul proiectarii ilustrat in figura 15.10 cu
urmatorul program MATLAB in care ![]() si
si ![]() .
.
Fe=8000; f=[600 800]; a=[1 0];
[n, f0, a0, w]=remezord(f, a, [0.01 0.001], Fe);
n
b=remez(n, f0, a0, w); [h, w]=freqz(b, 1, 1024);
figure(1),
plot(w/pi, 20*log10(abs(h))); title('H(z)'), grid
N=2*length(b); be=zeros(1, N); be(1:2:N)=b;
[h2, w2]=freqz(be, 1, 1024);
figure(2),
plot(w2/pi, 20*log10(abs(h2))); title('G(z2)'); grid
[n, f0, a0, w]=remezord([300 3600], [1 0], [0.01 0.001], Fe);
n
b3=remez(3, f0, a0, w); [h3, w3]=freqz(b3, 1, 1024);
figure(3),
plot(w3/pi, 20*log10(abs(h3))); title('I(z)'); grid
b4=[b3, zeros(1, length(be)-length(b3))];
b5=conv(be, b4); [h5, w5]=freqz(b5, 1, 1024);
figure(4),
plot(w5/pi, 20*log10(abs(h5))),
title('I(z)G(z2)'); grid
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2026 - Toate drepturile rezervate -| |








