
| Aeronautica | Comunicatii | Drept | Informatica | Nutritie | Sociologie |
| Tehnica mecanica |
Comunicatii
|
|
Qdidactic » stiinta & tehnica » comunicatii Orbitele satelitilor GPS |
Orbitele satelitilor GPS
Orbitele satelitilor GPS
1 Introducere
Aplicatiile G.P.S. depind substantial de cunoasterea orbitelor satelitilor. Pentru pozitionarea absoluta a unui singur punct, erorile orbitelor satelitilor influenteaza puternic precizia determinarii pozitiei. Informatia continand elementele orbitale este transmisa de satelit ca parte a unui semnal emis sau poate fi obtinuta (de obicei la multe saptamani dupa terminarea observatiilor) din cateva surse. Cuplarea dispozitivului de acces selectiv (S.A.), cu care sunt echipati satelitii blocului II, poate conduce la o degradare a orbitei emise in limita de la 30m la 50m. Este posibil ca din diverse motive, proprietarul sistemului sa nu furnizeze efemeride precise nici macar cu intarziere. Comunitatea civila si nu numai ea, trebuie sa-si genereze propriile efemeride precise ale satelitilor.
Acest capitol face o trecere in revista a teoriei orbitale, cu accentuarea orbitelor G.P.S. si pune bazele calculului parametrilor orbitali.
2 Descrierea orbitei
2.1 Miscarea kepleriana
Parametri orbitali
Presupunem doua puncte materiale m1 si m2 separate de distanta r. Considerand pentru moment doar forta de atractie intre mase si aplicand principiile mecanicii newtoniene, miscarea masei m2 relativ la m1 este definita de o ecuatie diferentiala de ordin II ,
![]() , (1) in care:
, (1) in care:
![]() vectorul de pozitie,
cu
vectorul de pozitie,
cu ![]() ;
;
![]() vectorul acceleratie relativa;
vectorul acceleratie relativa;
G constanta gravitatiei universale.
In cazul miscarii unui satelit artificial al Pamantului, intr-o prima aproximatie, ambele corpuri pot fi considerate ca mase punctiforme si masa satelitului poate fi neglijata. Produsul dintre G si masa Pamantului MP este notat cu si este cunoscut ca un parametru de definitie a sistemului de referinta WGS-8 Conform tabelului 3.1, = G.MP = 3986005.108 m3.s-2
Rezolvarea analitica a ecuatiei diferentiale (1) poate fi gasita in tratatele de mecanica cereasca si conduce la binecunoscuta miscare kepleriana definita de sase parametri orbitali, care corespund celor sase constante rezultate prin integrarea de doua ori a ecuatiei vectoriale (1).
Orbitele satelitilor pot fi restrictionate la miscarea eliptica, cei 6 parametri fiind enumerati in tabelul 1. Punctul cel mai apropiat in raport cu centrul de masa al Pamantului este numit perigeu iar pozitia cea mai departata este numita apogeu. Intersectiile dintre planele ecuatorial si orbital cu sfera sunt denumite noduri, nodul ascendent constituind punctul de traversare spre nord a ecuatorului. O reprezentare grafica a orbitei Kepleriene este data in figura 1.
Notand cu P perioada de rotatie a satelitului si cu a semiaxa mare a orbitei, viteza unghiulara medie a satelitului n (cunoscuta si sub numele de anomalie mijlocie) este data de cea de-a 3a lege a lui Kepler:
![]() (2)
(2)
Tabelul 1. Parametrii orbitei kepleriene.
|
Parametri |
Semnificatia |
|
W |
Ascensia dreapta a nodului ascendent |
|
i |
Inclinarea planului orbitei fata de ecuator |
|
w |
Argumentul perigeului |
|
a |
Semiaxa mare a orbitei |
|
e |
Excentricitatea numerica a orbitei |
|
T0 |
Epoca (momentul) trecerii la perigeu |
Pentru orbitele satelitilor GPS, semiaxa mare nominala este a=26.560km. Inlocuirea acestei valori in (2) conduce la o perioada orbitala de 12 ore siderale. Punctele terestre subsatelit se repeta asadar in fiecare zi siderala.
Pozitia instantanee a satelitului pe orbita proprie este descrisa de o marime unghiulara cunoscuta (din motive istorice) sub numele de anomalie. Tabelul 2 contine anomaliile uzual folosite. Anomalia mijlocie M(t) este o abstractizare matematica, in timp ce anomalia excentrica E(t) si cea adevarata v(t) pot fi reprezentate geometric.
Cele trei anomalii sunt date de relatiile
![]() (3)
(3)
![]() (4)
(4)
![]() , (5)
, (5)
unde e reprezinta excentricitatea numerica a orbitei.


Figura 1. Orbita kepleriana
Tabelul 2. Anomaliile orbitei kepleriene
|
Notatia |
Anomalia |
|
M(t) |
Anomalia medie (mijlocie) |
|
E(t) |
Anomalia excentrica |
|
v(t) |
Anomalia adevarata |
Ecuatia (3) are caracter de definitie si arata ca anomalia mijlocie poate fi folosita in locul lui T0 ca parametru al orbitei. Ecuatia (4) este cunoscuta ca ecuatia lui Kepler si este obtinuta prin integrarea analitica a ecuatiei (1). Ecuatia (5) are o interpretare geometrica, aratata mai jos.
Pentru a exemplifica diferentele dintre cele trei anomalii, presupunem o orbita cu o perioada semidiurna si o excentricitate e = 0,1. La epoca '3h dupa trecerea la perigeu', anomalia mijlocie este M = 90o,000. Calculul anomaliei excentrice necesita iteratii si da E=95o,7012. Anomalia adevarata este v=101o,3838.
Reprezentarea orbitei
Sistemele
de coordonate ![]() , i=1,2 care
definesc planele orbitale sunt reprezentate in figura 1. Vectorul de
pozitie
, i=1,2 care
definesc planele orbitale sunt reprezentate in figura 1. Vectorul de
pozitie ![]() si vectorul
vitezei satelitului
si vectorul
vitezei satelitului ![]() pot fi exprimati
prin intermediul anomaliei excentrice la fel de bine ca si prin intermediul anomaliei adevarate:
pot fi exprimati
prin intermediul anomaliei excentrice la fel de bine ca si prin intermediul anomaliei adevarate:
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
Componentele
vectorului ![]() sunt puse in
evidenta in figura 1, unde
semiaxa mica b este inlocuita cu
sunt puse in
evidenta in figura 1, unde
semiaxa mica b este inlocuita cu
![]() .
.
Distanta
geocentrica r=r(E) corespunde normei ![]() .
.
Reprezentarea r=r(v) este cunoscuta ca ecuatie polara a elipsei.
Ecuatia (5) poate fi verificata. Pentru aceasta se utilizeaza (6) si (7) precum si identitatea:
![]() .
.
Derivarea
vectorului viteza ![]() =
=![]() (E) necesita
cunoasterea derivatei in raport cu timpul a anomaliei excentrice dE/dt=n.a/r. Acest rezultat
este obtinut diferentiind ecuatia lui Kepler si inlocuind in
ecuatia (7).
(E) necesita
cunoasterea derivatei in raport cu timpul a anomaliei excentrice dE/dt=n.a/r. Acest rezultat
este obtinut diferentiind ecuatia lui Kepler si inlocuind in
ecuatia (7).
Derivarea
vectorului ![]() =
=![]() (v) este mult mai
laborioasa si rezultatul este dat fara demonstratie. Norma lui
(v) este mult mai
laborioasa si rezultatul este dat fara demonstratie. Norma lui ![]() (viteza radiala
(viteza radiala ![]() ) poate fi obtinuta din ambele reprezentari
) poate fi obtinuta din ambele reprezentari ![]() (E) sau
(E) sau ![]() (v). Calculul lui
(v). Calculul lui ![]() (E) este foarte
simplu, ca de altfel si deducerea expresiei lui
(E) este foarte
simplu, ca de altfel si deducerea expresiei lui ![]() (v). Ecuatia (9)
poate fi ridicata la patrat si impartita cu
relatia de legatura intre energia cinetica (in partea
stanga) si energia potentiala (in partea dreapta),
tinand cont ca a este prin
definitie o constanta. Prin urmare, ecuatia (9) poate fi
recunoscuta ca lege a conservarii energiei in sistemul
Pamant-satelit.
(v). Ecuatia (9)
poate fi ridicata la patrat si impartita cu
relatia de legatura intre energia cinetica (in partea
stanga) si energia potentiala (in partea dreapta),
tinand cont ca a este prin
definitie o constanta. Prin urmare, ecuatia (9) poate fi
recunoscuta ca lege a conservarii energiei in sistemul
Pamant-satelit.
Transformarea
lui ![]() sau
sau ![]() in sistemul ecuatorial
in sistemul ecuatorial
![]() este realizata
cu ajutorul unei matrice de rotatie
este realizata
cu ajutorul unei matrice de rotatie
![]() si rezulta
vectorii notati cu
si rezulta
vectorii notati cu ![]() si
si ![]() . Indicele superior 'S'
(satelit) nu s-a mai pus, pentru simplitatea scrierii. Vectorii exprimati
in sistemul orbital pot fi considerati ca vectori tridimensionali pentru
transformare. De aceea, axele
. Indicele superior 'S'
(satelit) nu s-a mai pus, pentru simplitatea scrierii. Vectorii exprimati
in sistemul orbital pot fi considerati ca vectori tridimensionali pentru
transformare. De aceea, axele ![]() ,
,![]() (continute in planul orbitei) sunt completate cu o
axa
(continute in planul orbitei) sunt completate cu o
axa ![]() care este
ortogonala pe planul orbitei. Pentru ca
care este
ortogonala pe planul orbitei. Pentru ca ![]() si
si ![]() sunt vectori in planul
orbitei (reprezentat de
sunt vectori in planul
orbitei (reprezentat de ![]() ,
,![]() ), componentele lor pe axa
), componentele lor pe axa ![]() sunt nule.
sunt nule.
Transformarea este definita de relatiile
![]() , (10)
, (10)
unde matricea R este compusa din trei matrice de rotatie aplicate succesiv, conform fig. 1, si este data de:
R=R3 R1 R3

![]() (11)
(11)
Coloanele
matricii ortogonale ![]() contin
componentele a 3 vectori care sunt chiar axele sistemului ecuatorial
contin
componentele a 3 vectori care sunt chiar axele sistemului ecuatorial ![]() in care sunt
reprezentate coordonatele orbitale. Pentru a transforma sistemul stelar
in care sunt
reprezentate coordonatele orbitale. Pentru a transforma sistemul stelar ![]() in sistemul terestru
in sistemul terestru ![]() este necesara o
rotatie aditionala cu unghiul q0 (timpul sideral Greenwich). Prin urmare,
matricea transformarii devine:
este necesara o
rotatie aditionala cu unghiul q0 (timpul sideral Greenwich). Prin urmare,
matricea transformarii devine:
R'=R3 R3 R1 R3 . (12)
Produsul R3 R3 poate fi exprimat de o matrice simpla R3 unde l=-0. Astfel, ecuatia (12) poate fi folosita sub forma:
R'=R3 R1 R3 (13)
Matricea R' corespunde matricei R daca in ecuatia (11) parametrul este inlocuit cu l.
Transformarea inversa ecuatiilor (10) urmareste obtinerea parametrilor keplerieni din vectorii pozitiei si vitezei (cunoscuti), amandoi exprimati in sistemul ecuatorial Xi. Din punct de vedere matematic, avem o problema cu valoare initiala pentru rezolvarea ecuatiei diferentiale (1). Pentru solutionare, se tine cont de faptul ca distantele si unghiurile sunt invariante in raport cu rotatiile. Se pot scrie deci urmatoarele ecuatii:
 (14)
(14)
Prin inlocuirea in ultimele doua relatii a ecuatiilor (6) si (8) se obtin:
produsul
scalar : ![]() ; (15)
; (15)
produsul
vectorial : ![]() . (16)
. (16)
Transformarea
inversa poate fi rezolvata dupa un algoritm prezentat in
continuare. Pentru inceput, cu ![]() si
si ![]() date, se
calculeaza distanta geocentrica r si viteza
date, se
calculeaza distanta geocentrica r si viteza ![]() . Cu aceste doua cantitati, semiaxa mare a se poate deduce din relatia (9).
Cu a si r determinate, se pot calcula e
cosE folosind ecuatia
(7) si e sinE cu relatia (15). Prin urmare, pot
fi calculate excentricitatea e,
anomalia excentrica E si
apoi anomaliile mijlocie si adevarata (M si v). Produsul
vectorial al vectorilor
. Cu aceste doua cantitati, semiaxa mare a se poate deduce din relatia (9).
Cu a si r determinate, se pot calcula e
cosE folosind ecuatia
(7) si e sinE cu relatia (15). Prin urmare, pot
fi calculate excentricitatea e,
anomalia excentrica E si
apoi anomaliile mijlocie si adevarata (M si v). Produsul
vectorial al vectorilor ![]() si
si ![]() este echivalent cu
vectorul c al momentului
unghiular si este directionat perpendicular pe planul orbitei. De
aceea, vectorul c, dupa
normalizare, este identic cu vectorul e3
din ecuatia (11); de aici pot fi dedusi parametrii i si l. Prin introducerea normei vectorului c in (16), pot fi verificati parametrii anterior calculati a si e. Pentru determinarea lui ,
este definit vectorul unitate
este echivalent cu
vectorul c al momentului
unghiular si este directionat perpendicular pe planul orbitei. De
aceea, vectorul c, dupa
normalizare, este identic cu vectorul e3
din ecuatia (11); de aici pot fi dedusi parametrii i si l. Prin introducerea normei vectorului c in (16), pot fi verificati parametrii anterior calculati a si e. Pentru determinarea lui ,
este definit vectorul unitate
k = ( cos l sin l 0 )T ,
directionat catre nodul ascendent (indicele superior T semnifica transpunerea).
Din figura 1 putem obtine relatiile:
![]() .k
= r cos(+v)
si
.k
= r cos(+v)
si ![]() .X3
= r sin i sin(+v) .
.X3
= r sin i sin(+v) .
Marimile r, v, i, fiind deja cunoscute, cele doua ecuatii pot fi rezolvate pentru obtinerea lui
Exemplu numeric. Consideram o orbita satelitara cu urmatorii parametri:
a = 26000 km; = -140 l = 110
e = 0,1; i = 60
Pentru calculul vectorilor de pozitie si viteza in sistemul ecuatorial terestru la o anumita epoca, la care anomalia excentrica a satelitului este E=45 , vectorii sunt mai intai calculati in planul orbital folosind relatiile (6) (9). Apoi este realizata transformarea in sistemul ecuatorial cu ajutorul relatiilor (10), folosind matricea de rotatie R'. Rezultatele finale sunt:
![]() = ( 11465 3818 -20923 )T Km
= ( 11465 3818 -20923 )T Km
![]() = ( -1,2651 3,9960 -0,3081 )T Km.s-1
= ( -1,2651 3,9960 -0,3081 )T Km.s-1
Este recomandabil sa realizati
dumneavoastra transformarea inversa, considerand ![]() si
si ![]() cunoscuti si
sa determinati parametrii orbitei kepleriene.
cunoscuti si
sa determinati parametrii orbitei kepleriene.
In afara
sistemului orbital fix ei
se poate defini un alt sistem ortonormal ![]() . Acest sistem se roteste in jurul axei e3 deoarece axa
. Acest sistem se roteste in jurul axei e3 deoarece axa ![]() trebuie sa
ramana permanent indreptata catre pozitia instantanee
a satelitului. De aceea, vectorii unitate
trebuie sa
ramana permanent indreptata catre pozitia instantanee
a satelitului. De aceea, vectorii unitate ![]() pot fi
obtinuti din vectorii de pozitie si viteza, cu
relatiile:
pot fi
obtinuti din vectorii de pozitie si viteza, cu
relatiile:
![]() ;
; ![]() ;
; ![]() . (17)
. (17)
Este de
remarcat faptul ca vectorii de baza ![]() corespund vectorilor
coloana ai matricei de rotatie modificata
corespund vectorilor
coloana ai matricei de rotatie modificata ![]() , obtinuta din (11) prin inlocuirea parametrului
cu (+v).
, obtinuta din (11) prin inlocuirea parametrului
cu (+v).
O
modificare d![]() a vectorului de pozitie se va transforma in sistemul
orbital
a vectorului de pozitie se va transforma in sistemul
orbital ![]() intr-un vector e = , componentele sale fiind calculate de-a lungul axelor
intr-un vector e = , componentele sale fiind calculate de-a lungul axelor ![]() :
:
e1 = ![]() .d
.d![]() componenta
radiala;
componenta
radiala;
e2 = ![]() .d
.d![]() componenta in
lungul traiectoriei; (18)
componenta in
lungul traiectoriei; (18)
e3 = ![]() .d
.d![]() componenta in
afara planului orbitei.
componenta in
afara planului orbitei.
Invers, d![]() poate fi calculat daca vectorul e este dat. Rezolvarea consta in inversarea ecuatiilor (18), care conduce la
poate fi calculat daca vectorul e este dat. Rezolvarea consta in inversarea ecuatiilor (18), care conduce la
![]() . (19)
. (19)
Exemplu numeric. Consideram o modificare
d![]() = ( 0,1 1,0 -0,5 )T
[km]
= ( 0,1 1,0 -0,5 )T
[km]
a pozitiei satelitului. Aplicand ecuatiile (17) si (18) rezulta:
e=( 0,638 0,914 0,128 )T [km].
Relatii diferentiale
Derivatele
lui ![]() si
si ![]() in raport cu cei
sase parametri keplerieni sunt necesare intr-un capitol ulterior.
Diferentierea poate fi separata in doua grupuri deoarece in
relatiile (10) vectorii
in raport cu cei
sase parametri keplerieni sunt necesare intr-un capitol ulterior.
Diferentierea poate fi separata in doua grupuri deoarece in
relatiile (10) vectorii ![]() si
si ![]() depind numai de
parametrii a, e, T0 , pe
cand matricea R este
functie doar de parametrii ramasi , i, .
depind numai de
parametrii a, e, T0 , pe
cand matricea R este
functie doar de parametrii ramasi , i, .
Pentru a
obtine derivatele lui ![]() si
si ![]() , este avantajos sa diferentiem vectorii
exprimati in functie de anomalia excentrica. Ca un prim pas,
sunt calculate derivatele marimilor n,
E,
r in raport cu parametrii a, e, T0.
, este avantajos sa diferentiem vectorii
exprimati in functie de anomalia excentrica. Ca un prim pas,
sunt calculate derivatele marimilor n,
E,
r in raport cu parametrii a, e, T0.
Prin diferentirea relatiei (2) obtinem:
![]() ;
; ![]() ;
; ![]() . (20)
. (20)
Diferentiind ecuatia lui Kepler (4) si inlocuind expresiile (20) obtinem:
![]() ;
; ![]() ;
; ![]() . (21)
. (21)
In final, diferentierea relatiei (7) permite obtinerea valorilor:
![]()
![]() (22)
(22)
![]() .
.
Din (6) si (8) si dupa o transformare algebrica in care se efectueaza substitutia dm = - n dT0 se obtin relatiile:
 (23)
(23)
 (24)
(24)
 (25)
(25)
 (26)
(26)
 (27)
(27)
![]() . (28)
. (28)
Considerand relatia (11), diferentierea matricei R in raport cu parametrii , i, este simpla si nu ridica probleme. Prin urmare, relatiile diferentiale sunt date de:
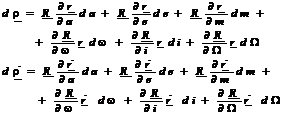 (29)
(29)
![]() Deoarece
anomalia medie si cea excentrica sunt continute in
ecuatiile (23) la (28), aceste derivate in raport cu parametrii a, e,
m, sunt dependente de timp.
Datorita aparitiei lui
Deoarece
anomalia medie si cea excentrica sunt continute in
ecuatiile (23) la (28), aceste derivate in raport cu parametrii a, e,
m, sunt dependente de timp.
Datorita aparitiei lui ![]() si
si ![]() , toti termenii ecuatiilor (29) sunt
dependenti de timp, chiar daca derivatele matricei R in raport cu , i, sunt constante.
, toti termenii ecuatiilor (29) sunt
dependenti de timp, chiar daca derivatele matricei R in raport cu , i, sunt constante.
2.2 Miscarea perturbata
Orbita
kepleriana este o orbita teoretica si nu include
perturbatiile care duc la modificarea parametrilor sai. In
consecinta, acceleratiile perturbatoare d![]() trebuie adaugate in ecuatia (1), care este
scrisa in sistem ecuatorial. Miscarea perturbata este
exprimata printr-o ecuatie diferentiala neomogena de
ordinul doi:
trebuie adaugate in ecuatia (1), care este
scrisa in sistem ecuatorial. Miscarea perturbata este
exprimata printr-o ecuatie diferentiala neomogena de
ordinul doi:
![]() . (30)
. (30)
Trebuie
tinut cont ca, pentru satelitii GPS, acceleratia ![]() corespunzatoare
fortei centrale de atractie /2 este cel
putin de 104 ori mai mare decat acceleratia perturbatoare.
Astfel, pentru solutionarea analitica a ecuatiei (30), teoria
perturbatiilor poate fi aplicata initial doar in partea
omogena a ecuatiei. Aceasta conduce la o orbita kepleriana
definita de sase parametri pi0,
i=1,,6 la epoca de
referinta t0.
Fiecare acceleratie perturbatoare d
corespunzatoare
fortei centrale de atractie /2 este cel
putin de 104 ori mai mare decat acceleratia perturbatoare.
Astfel, pentru solutionarea analitica a ecuatiei (30), teoria
perturbatiilor poate fi aplicata initial doar in partea
omogena a ecuatiei. Aceasta conduce la o orbita kepleriana
definita de sase parametri pi0,
i=1,,6 la epoca de
referinta t0.
Fiecare acceleratie perturbatoare d![]() cauzeaza variatii temporale
cauzeaza variatii temporale ![]() =dpi0/dt ale parametrilor orbitei. Prin
urmare, la o epoca arbitrara t,
parametrii pi descriind
asa numita elipsa osculatoare
sunt dati de:
=dpi0/dt ale parametrilor orbitei. Prin
urmare, la o epoca arbitrara t,
parametrii pi descriind
asa numita elipsa osculatoare
sunt dati de:
pi = pi0 + ![]() (t-t0) (31)
(t-t0) (31)
Pentru a
obtine derivatele in raport cu timpul ![]() , putem face o comparatie intre miscarea
kepleriana si miscarea perturbata. In primul caz,
parametrii pi sunt
constanti pe cand in al doilea caz ei sunt dependenti de timp.
Astfel, pentru vectorii de pozitie si viteza ai
miscarii perturbate putem scrie:
, putem face o comparatie intre miscarea
kepleriana si miscarea perturbata. In primul caz,
parametrii pi sunt
constanti pe cand in al doilea caz ei sunt dependenti de timp.
Astfel, pentru vectorii de pozitie si viteza ai
miscarii perturbate putem scrie:
![]() (32)
(32)
Diferentiind ambele ecuatii in raport cu timpul si tinand cont de (30) obtinem:
 (33)
(33)
![]() . (34)
. (34)
Incepand cu orice epoca t poate fi definita o elipsa (osculatoare), ecuatiile (33) si (34) tinand de miscarea kepleriana. Evident, o echivalenta este obtinuta din conditiile urmatoare:
 (35)
(35)
In cele ce urmeaza, pentru simplitate, este considerata doar acceleratia perturbatoare. Cele doua ecuatii vectoriale (35) corespund la sase ecuatii liniare, care in notatia vectoriala sunt date de:
![]() (36)
(36)
unde


![]()
![]()
Matricea
A (6x6) necesita derivatele lui ![]() si
si ![]() in raport cu
parametrii keplerieni, care au fost explicitati la punctul 2.1,
relatia (29). Vectorul l
(6x1) contine
acceleratia perturbatoare. Cele sase derivate in raport timpul ale
necunoscutelor apar in vectorul u (6x1) .
in raport cu
parametrii keplerieni, care au fost explicitati la punctul 2.1,
relatia (29). Vectorul l
(6x1) contine
acceleratia perturbatoare. Cele sase derivate in raport timpul ale
necunoscutelor apar in vectorul u (6x1) .
Inversarea sistemului (36) conduce la ecuatiile
Lagrange, in care intervine potentialul perturbator R, asociat cu acceleratia perturbatoare prin relatia ![]() =grad R:
=grad R:
![]()
![]()
![]() (37)
(37)

![]()
![]() .
.
Sistemul
(37) este nerezolvabil pentru e=0 sau
i=0. Singularitatea poate fi
evitata prin utilizarea parametrilor auxiliari. Ecuatiile Lagrange
presupun ca potentialul perturbator R este exprimat in functie de parametrii keplerieni. Cand
acceleratia ![]() este reprezentata
prin componentele Ki in
lungul axelor
este reprezentata
prin componentele Ki in
lungul axelor ![]() , sistemul (37) poate fi transformat folosind identitatea
, sistemul (37) poate fi transformat folosind identitatea
![]() . (38)
. (38)
Transformari simple dar laborioase conduc la ecuatiile lui Gauss, (39).
Se
observa ca in variatiile temporale ![]() si
si ![]() apare doar componenta
ortogonala pe planul orbitei K3,
iar variatiile
apare doar componenta
ortogonala pe planul orbitei K3,
iar variatiile ![]() ,
, ![]() ,
, ![]() sunt afectate de
ambele coponente in planul orbital, K1
si K2.
sunt afectate de
ambele coponente in planul orbital, K1
si K2.
![]()
![]()
![]() (39)
(39)
![]()
![]()
![]() .
.
2.3 Acceleratii perturbatoare
Fata de cele prezentate anterior, in realitate sunt mai multe acceleratii perturbatoare raspunzatoare de variatiile temporale ale elementelor Kepleriene. La prima vedere, ele pot fi impartite in doua categorii, dupa natura: gravitationale si negravitationale (vezi tabelul 3).
Tabelul 3. Surse de acceleratii perturbatoare
|
Gravitationale |
Nesfericitatea Pamantului Atractia mareica (directa si indirecta) |
|
Negravitationale |
Presiunea radiatiei solare (directa si indirecta) Rezistenta aerului Efecte relativiste Alte surse (vant solar, forte magnetice etc.) |
Deoarece orbitele satelitilor GPS sunt situate la o altitudine aproximativa de 20.000 Km, efectele indirecte ale contactului cu aerul pot fi neglijate. Pe de alta parte, forma (si deci sectiunea) satelitilor este neregulata si face mai dificila modelarea radiatiei solare. Varietatea materialelor folosite pentru sateliti, fiecare cu un coeficient de absorbtie a caldurii diferit, are ca rezultat acceleratii perturbatoare aditionale complicate. De asemenea, acceleratii pot apare din fisuri ale containerului cu gaz de propulsie.
Pentru a
avea o idee despre acceleratiile perturbatoare, consideram un exemplu
presupunand o perturbatie constanta ![]() , actionand asupra unui satelit GPS. Schimbarile pe
care le provoaca in pozitia satelitului rezulta din dubla
integrare in raport cu timpul t
si da dr =
, actionand asupra unui satelit GPS. Schimbarile pe
care le provoaca in pozitia satelitului rezulta din dubla
integrare in raport cu timpul t
si da dr =![]() (t2/2).
Inlocuind valoarea numerica t
12h, obtinem schimbarea dupa o
revolutie si anume dr 1m. Aceasta valoare este destul de apropiata de
realitate.
(t2/2).
Inlocuind valoarea numerica t
12h, obtinem schimbarea dupa o
revolutie si anume dr 1m. Aceasta valoare este destul de apropiata de
realitate.
Nesfericitatea Pamantului. Potentialul terestru V poate fi reprezentat printr-o dezvoltare in serie de armonici sferice:
 (40)
(40)
unde aP este semiaxa mare a Pamantului, r este distanta geocentrica a satelitului, iar , sunt latitudinea si longitudinea acestuia. Jn, Jnm, Knm sunt coeficientii zonali si cubici ai dezvoltarii armonice, cunoscuti din modelul terestru. In sfarsit, Pn sunt polinoamele Legendre si Pnm sunt functiile Legendre asociate.
Primul termen al partii drepte a ecuatiei (40), /r, reprezinta potentialul V0 pentru Pamantul considerat sferic; gradientul sau grad(/r) = (/r3) r este considerat forta centrala a miscarii kepleriene. Deci potentialul perturbator este dat de diferenta R = V - V0 . (41)
Mai jos se va arata ca acceleratia perturbatoare datorata lui J2, termenul reprezentand turtirea, este mai mica de 104 ori decat acceleratia datorata lui Vo. Pe de alta parte, termenul turtirii este aproximativ cu trei ordine de marime mai mare decat orice alt coeficient. In urma unor evaluari a rezultat ca o submultime completa a coeficientilor mai mari dacat rangul si ordinul opt este suficienta pentru arcele catorva revolutii.
O
estimare numerica a acceleratiei centrale a satelitilor GPS ne
da ![]() . Acceleratia corespunzand potentialului
perturbator R este data de
relatia
. Acceleratia corespunzand potentialului
perturbator R este data de
relatia![]() .
.
Latitudinea satelitului poate atinge doar =55o,
adica valoarea inclinarii propriei orbite. Maximul functiei P2(sin)=˝(3sin2-1)
este prin urmare 0,5. In final, cu J2 1,1.10-3, conform tabelului 3.1,
este obtinuta valoarea numerica ![]() .
.
Efecte mareice. Consideram un corp ceresc
cu masa punctuala mc
si definit de vectorul de pozitie geocentrica ![]() , conform figurii 2. Observam ca unghiul geocentric
z (dintre corpul ceresc si satelit)
poate fi exprimat ca o functie de
, conform figurii 2. Observam ca unghiul geocentric
z (dintre corpul ceresc si satelit)
poate fi exprimat ca o functie de ![]() si
si ![]() , vectorul de pozitie geocentrica a satelitului:
, vectorul de pozitie geocentrica a satelitului: ![]() (42)
(42)
Masa aditionala exercita atractie asupra Pamantului si asupra satelitului. Pentru evidentierea miscarii perturbate a satelitului in jurul Pamantului, este edificatoare diferenta celor doua acceleratii, deci acceleratia perturbatoare este data de relatia (43).

Figura 2. Problema celor trei corpuri
![]() (43)
(43)
Dintre toate corpurile ceresti din sistemul solar, doar Soarele si Luna trebuie considerate, efectul planetelor putand fi neglijat. Vectorii de pozitie geocentrica ai Soarelui si Lunii sunt obtinuti din evaluarea expresiilor analitice ale miscarilor lor.
Maximul acceleratiei perturbatoare este atins cand cele trei corpuri din figura 2 sunt situate in linie dreapta. In acest caz, ecuatia (43) se reduce la:
![]()
Pentru o evaluare a ordinului de marime, sunt inlocuite valorile numerice corespunzatoare Soarelui (Gmc 1,3.1020m3.s-2 ; c 1,5.1011m) si Lunii (Gmc 4,9.1012m3.s-2 ; c 3,8.108 m). Valorile numerice rezultate ale acceleratiei perturbatoare sunt 2.10-6 m.s-2 pentru Soare si 5.10-6 m.s-2 pentru Luna.
Separat de efectele directe ale corpurilor ceresti cu efect mareic, trebuie luate in considerare si efectele indirecte, corespunzatoare mareelor terestre (deformatii ale partii solide a Pamantului) si mareelor oceanice. Considerand doar potentialul mareic de gradul doi W2, potentialul perturbator R datorat deformatiilor legate de mareele terestre este dat de relatia
![]() , (44)
, (44)
in care k 0,3 este unul din numerele lui Love. Acceleratia imprimata satelitului este de ordinul 10-9
m.s-2. Efectul indirect corespunzator mareelor
oceanice este mult mai greu de modelat. Sunt necesare harti marine cu
distributia fluxurilor oceanice. In plus, sunt necesari coeficientii
calculati de Farell, care
descriu reactia Pamantului solid la deplasarea maselor de apa
oceanica. Acceleratia perturbatoare este tot de ordinul a 10-9 m.s-2.
Ca o consecinta a deformatiei mareice si a repartitiei
maselor oceanice, vectorul de pozitie geocentrica a receptorului (![]() ) variaza in timp. Aceste variatii trebuie luate in
considerare cand se determina erorile sistematice care depind de receptor.
) variaza in timp. Aceste variatii trebuie luate in
considerare cand se determina erorile sistematice care depind de receptor.
Presiunea
radiatiei solare
Acceleratia perturbatoare datorata presiunii radiatiei solare
are doua componente. O componenta principala ![]() , dirijata dinspre Soare si o componenta mai
mica
, dirijata dinspre Soare si o componenta mai
mica ![]() ce se manifesta de-a lungul axei y a satelitului. Aceasta este o axa ortogonala pe doi
vectori: cel care uneste satelitul cu Soarele si cel definit de
antena de emisie (care in mod normal este directionata catre
centrul Pamantului).
ce se manifesta de-a lungul axei y a satelitului. Aceasta este o axa ortogonala pe doi
vectori: cel care uneste satelitul cu Soarele si cel definit de
antena de emisie (care in mod normal este directionata catre
centrul Pamantului).
Componenta principala este modelata de relatia
![]() , (45)
, (45)
in care ![]() este vectorul de
pozitie geocentrica a Soarelui. Factorul K depinde liniar de radiatia solara constanta
este vectorul de
pozitie geocentrica a Soarelui. Factorul K depinde liniar de radiatia solara constanta ![]() , de un factor Cr
definind proprietatile de reflexie ale satelitului si de
raportul arie-masa al satelitului.
Cantitatea este un factor de
eclipsa, care este 0 (zero) cand satelitul este in umbra
Pamantului; aceasta se intampla de doua ori intr-un an, cand
Soarele este in sau langa planul orbital. O astfel de
eclipsa dureaza aproximativ o ora. Factorul de eclipsa este
unu cand satelitul este luminat de Soare si 0<<1 cand se
afla in regiunile de penumbra.
, de un factor Cr
definind proprietatile de reflexie ale satelitului si de
raportul arie-masa al satelitului.
Cantitatea este un factor de
eclipsa, care este 0 (zero) cand satelitul este in umbra
Pamantului; aceasta se intampla de doua ori intr-un an, cand
Soarele este in sau langa planul orbital. O astfel de
eclipsa dureaza aproximativ o ora. Factorul de eclipsa este
unu cand satelitul este luminat de Soare si 0<<1 cand se
afla in regiunile de penumbra.
Marimea
lui ![]() este de ordinul 10-7 m.s-2.
Valori precise pentru factorii K
si sunt necesare doar pentru arce mici. Modelarea lor este extrem
de dificila deoarece factorul
este de ordinul 10-7 m.s-2.
Valori precise pentru factorii K
si sunt necesare doar pentru arce mici. Modelarea lor este extrem
de dificila deoarece factorul ![]() variaza aleator
in timpul anului iar utilizarea pentru satelit a unui singur factor Cr (constant) nu este
adecvata. Desi masa pe orbita este bine cunoscuta, forma
neregulata a satelitului nu permite o determinare exacta a raportului
arie-masa. O problema suplimentara este modelarea penumbrei
Pamantului si definirea factorului de eclipsa, in particular
pentru zona de tranzitie dintre iluminare si umbra.
variaza aleator
in timpul anului iar utilizarea pentru satelit a unui singur factor Cr (constant) nu este
adecvata. Desi masa pe orbita este bine cunoscuta, forma
neregulata a satelitului nu permite o determinare exacta a raportului
arie-masa. O problema suplimentara este modelarea penumbrei
Pamantului si definirea factorului de eclipsa, in particular
pentru zona de tranzitie dintre iluminare si umbra.
Componenta
![]() , numita si y-deplasare,
se considera a fi cauzata de erorile de aliniere a panourilor solare
si de radiatia termica de-a lungul axei y. Deoarece marimea acestei erori poate ramane
constanta cateva saptamani, de obicei este introdusa ca
parametru necunoscut care este aflat in cursul determinarii orbitei. De
retinut ca aceasta eroare este cu doua ordine de
marime mai mica decat termenul principal.
, numita si y-deplasare,
se considera a fi cauzata de erorile de aliniere a panourilor solare
si de radiatia termica de-a lungul axei y. Deoarece marimea acestei erori poate ramane
constanta cateva saptamani, de obicei este introdusa ca
parametru necunoscut care este aflat in cursul determinarii orbitei. De
retinut ca aceasta eroare este cu doua ordine de
marime mai mica decat termenul principal.
Partea de presiune a radiatiei solare care este reflectata inapoi de suprafata Pamantului, creaza un efect numit albedo (in teledetectie acest termen defineste coeficientul de reflexie). In cazul GPS, acceleratiile perturbatoare asociate sunt mai mici decat y-deplasarea si prin urmare pot fi neglijate.
Efecte relativiste. Efectul relativist asupra orbitei satelitului este cauzat de campul gravitational terestru si da o crestere a acceleratiei perturbatoare exprimata aproximativ de ecuatia
![]() , (46)
, (46)
unde c este viteza luminii. O estimare numerica da un ordin de marime al acceleratiei perturbatoare de 3.10-10 m.s-2. Acest efect este mai mic decat cele indirecte cu un ordin de marime si este mentionat numai pentru a ne convinge ca este neglijabil.
3 Determinarea orbitei
Determinarea orbitei consta in esenta in determinarea parametrilor sai si a erorilor ceasului satelitar. In principiu, problema este inversa celei de navigatie sau determinarilor in scopuri geodezice.
Pentru o
statie R si un satelit GPS
notat S, se pot scrie doua ecuatii
fundamentale care dau distanta si respectiv viteza de
variatie a acesteia ![]() :
:
![]() (47)
(47)
![]() . (48)
. (48)
Vectorul de pozitie ![]() si vectorul
vitezei
si vectorul
vitezei ![]() ai satelitului sunt
considerati necunoscuti iar coordonatele locului de observatie
sunt presupuse cunoscute in sistemul geocentric.
ai satelitului sunt
considerati necunoscuti iar coordonatele locului de observatie
sunt presupuse cunoscute in sistemul geocentric.
In cele ce urmeaza erorile sistematice ale ceasului satelitar, dar si alti parametri, sunt neglijate. Este accentuata determinarea actuala a orbitelor, care se realizeaza in doi pasi. Mai intii se determina o orbita kepleriana, care este apoi imbunatatita prin luarea in considerare a acceleratiilor perturbatoare.
3.1 Orbita kepleriana
Pentru moment se considera ca ambii vectori ai satelitului, de pozitie si viteza, se obtin din observatii.
Vectorii de pozitie si viteza, cunoscuti la aceeasi epoca t, constituie datele unei probleme cu valori initiale, tratata in subcapitolul 2.1. Reamintim ca cei doi vectori contin cu totul sase componente, care permit calculul celor sase parametri keplerieni.
Vectorii
de pozitie sunt mult mai precis determinati si de aceea sunt
preferati pentru determinarile orbitale. Consideram ca la
epocile t1 si t2 s-au masurat doi
vectori de pozitie ![]() (t1)
si
(t1)
si ![]() (t2).
Aceste date sunt valorile la limita pentru solutia ecuatiei
diferentiale fundamentala de ordinul doi (1). O metoda
aproximativa pentru obtinerea parametrilor keplerieni foloseste
valori initiale definite pentru epoca mijlocie t=(t1+t2)/2:
(t2).
Aceste date sunt valorile la limita pentru solutia ecuatiei
diferentiale fundamentala de ordinul doi (1). O metoda
aproximativa pentru obtinerea parametrilor keplerieni foloseste
valori initiale definite pentru epoca mijlocie t=(t1+t2)/2:
 (49)
(49)
Rezolvarea riguroasa incepe cu calculul distantelor geocentrice:
 (50)
(50)
Versorul ![]() , perpendicular pe planul orbitei, este obtinut dintr-un
produs vectorial de forma
, perpendicular pe planul orbitei, este obtinut dintr-un
produs vectorial de forma
 (51)
(51)
si contine longitudinea l si unghiul de inclinare i, conform relatiilor (11) si (13). Asa cum a fost prezentat anterior, argumentul satelitului u=+v este definit ca unghiul dintre vectorul de pozitie al satelitului si vectorul nodului ascendent k = ( cos l sin l 0 )T . Prin urmare, relatia
![]() (52)
(52)
permite calculul valorilor ui, cu u2 > u1 intotdeauna. Conform (7), se pot scrie doua ecuatii
![]() (53)
(53)
in care parametrii a, e, sunt necunoscuti. Pentru ca acest sistem sa poata fi rezolvat, se atribuie parametrului (argumentul perigeului) valoarea 1. In urma rezolvarii sistemului, se obtin parametrii a si e ai orbitei. Cu considerat si ui sunt obtinute anomaliile adevarate vi=ui- si ulterior anomaliile mijlocii Mi. Acum, viteza unghiulara medie n poate fi calculata de doua ori, conform (2) si (3):
![]() . (54)
. (54)
Echivalenta se obtine variind . Aceasta procedura iterativa este tipica pentru problemele cu valori la limita. In final, epoca trecerii la perigeu T0 rezulta din relatia:
 . (55)
. (55)
Exemplu numeric.
Consideram doi vectori de pozitie ![]() si
si ![]() , amandoi reprezentati in sistemul ecuatorial terestru
, amandoi reprezentati in sistemul ecuatorial terestru ![]() si t=t2-t1=1h :
si t=t2-t1=1h :
![]() = (
11465 3818 -20923 ) km
= (
11465 3818 -20923 ) km ![]() = ( 5220 16754 -18421 ) km
= ( 5220 16754 -18421 ) km
Aplicarea relatiilor (50) la (55), omitand erorile de rotunjire, conduce la urmatorul set de parametri asociati elipsei kepleriene: a = 26000 km, e = 0.1, = - 140o, i = 60o, l = 110o si T0 = t1-1h,3183.
Daca
exista observatii cu caracter redundant, atunci parametrii orbitei
Kepleriene instantanee pot fi imbunatatiti. Pozitia
vectorului ![]() asociat elipsei de referinta se poate calcula,
pentru fiecare distanta fiind scrisa o ecuatie de forma:
asociat elipsei de referinta se poate calcula,
pentru fiecare distanta fiind scrisa o ecuatie de forma:
![]() . (56)
. (56)
Vectorul ![]() poate fi exprimat ca o
functie de parametrii keplerieni, conform (29). Deci (56)
contine incrementarile
diferentiale pentru cei sase parametri orbitali. O
imbunatatire a orbitei se poate obtine si in cursul
prelucrarii datelor GPS, daca in afara vectorilor de pozitie
geocentrica a punctelor de statie se considera necunoscute
si cantitatile diferentiale dpoi.
Aceasta metoda devine nesigura in cazul retelelor mici.
Uneori sunt considerate doar trei grade de libertate ale orbitei (se
considera necunoscut un vector al deplasarilor), procedura fiind
numita relaxarea orbitei.
poate fi exprimat ca o
functie de parametrii keplerieni, conform (29). Deci (56)
contine incrementarile
diferentiale pentru cei sase parametri orbitali. O
imbunatatire a orbitei se poate obtine si in cursul
prelucrarii datelor GPS, daca in afara vectorilor de pozitie
geocentrica a punctelor de statie se considera necunoscute
si cantitatile diferentiale dpoi.
Aceasta metoda devine nesigura in cazul retelelor mici.
Uneori sunt considerate doar trei grade de libertate ale orbitei (se
considera necunoscut un vector al deplasarilor), procedura fiind
numita relaxarea orbitei.
3.2 Orbita perturbata
Solutia analitica. Asa cum se stie din capitolele anterioare, miscarea perturbata este caracterizata de variatii temporale ale parametrilor orbitei. Expresiile analitice pentru aceste variatii sunt date de ecuatiile (37) sau (39).
Pentru a fi aplicabil in ecuatiile lui Lagrange, potentialul perturbator trebuie exprimat ca o functie de parametrii keplerieni. Pentru efectele nesfericitatii Pamantului, functiile Legendre din ecuatia (40) trebuie transformate. Relatia ce rezulta este:
![]() (57)
(57)
Reamintim ca n semnifica gradul iar m ordinul armonicelor sferice in dezvoltarea potentialului perturbator. Fiecare din functiile An, Fnmp, Gnpq contine doar un parametru al elipsei kepleriene. Numai functia Snmpq are in compunere mai multi parametri si poate fi exprimata prin una din relatiile:
![]() (58)
(58)
Considerand frecventa ![]() asociata
argumentului , avem
asociata
argumentului , avem
![]() , (59)
, (59)
relatie care ne ofera indicatii asupra spectrului perturbatiilor.
Conditiile
(n-2p) = (n-2p+q)
= m = 0 conduc la ![]() = 0, deci la variatii seculare; deoarece m=0, ele sunt cauzate de armonicele
zonale. Daca (n-2p) 0, variatiile depind de
= 0, deci la variatii seculare; deoarece m=0, ele sunt cauzate de armonicele
zonale. Daca (n-2p) 0, variatiile depind de ![]() si sunt de lunga perioda. In final,
conditiile (n-2p+q)
0 si/sau m 0 conduc la variatii de scurta perioada.
Valoarea intreaga (n-2p+q)
da frecventa in cicli pe revolutie iar m, frecventa in cicli pe zi.
si sunt de lunga perioda. In final,
conditiile (n-2p+q)
0 si/sau m 0 conduc la variatii de scurta perioada.
Valoarea intreaga (n-2p+q)
da frecventa in cicli pe revolutie iar m, frecventa in cicli pe zi.
O vedere aproximativa asupra spectrului perturbatiilor produse de campul gravific terestru asupra parametrilor keplerieni este prezentata in tabelul
Rezumand, coeficientii zonali de ordin par produc in primul rand variatii seculare iar coeficientii zonali de ordin impar sunt la originea perturbatiilor de lunga perioada. Coeficientii cubici sunt responsabili de termenii de scurta perioada.
In tabelul 4 putem observa ca variatiile de scurta perioada apar in fiecare parametru. Cu exceptia semiaxei mari, toti ceilalti parametri sunt afectati de perturbatiile de lunga perioada. Efectele seculare sunt continute doar in , , M. Un exemplu de expresii analitice pentru variatiile seculare, pentru influenta termenului turtirii J2, este urmatorul:
 (60)
(60)
Tabelul Perturbatiile datorate campului gravific terestru
|
Parametru |
Seculara |
Lunga perioada |
Scurta perioada |
|
a |
nu |
nu |
da |
|
e |
nu |
da |
da |
|
i |
nu |
da |
da |
|
|
da |
da |
da |
|
|
da |
da |
da |
|
M |
da |
da |
da |

Figura 3. Perturbatiile seculare cauzate de termenul de turtire J2
Prima ecuatie descrie regresia nodului in planul
ecuatorial, a doua ecuatie exprima rotatia perigeului iar a
treia ecuatie evidentiaza contributia la variatia
anomaliei mijlocii (![]() = n+
= n+![]() ). In cazul satelitilor GPS, sunt obtinute valorile
numerice
). In cazul satelitilor GPS, sunt obtinute valorile
numerice ![]() -0o,03 pe zi,
-0o,03 pe zi, ![]() 0o,01 pe zi si
0o,01 pe zi si ![]() 0. Rezultatul pentru
0. Rezultatul pentru ![]() se verifica
imediat deoarece, pentru inclinarea nominala i=55o, termenul 3cos2i-1 devine aproximativ zero. O reprezentare grafica a
perturbatiilor seculare este data in figura 3.
se verifica
imediat deoarece, pentru inclinarea nominala i=55o, termenul 3cos2i-1 devine aproximativ zero. O reprezentare grafica a
perturbatiilor seculare este data in figura 3.
O atentie speciala trebuie acordata efectelor de rezonanta care apar cand perioada de revolutie corespunde celei a potentialului gravific armonic. De aceea, satelitii GPS sunt plasati pe orbite de medie inaltime, pentru a exclude perioade foarte apropiate de jumatatea zilei siderale.
Potentialul mareic are o reprezentare armonica ce poate fi modelata analitic, analog efectului potentialului terestru. Se obtin expresii analitice pentru variatiile seculare ale ascensiei drepte a nodului si argumentului perigeului
Solutia
numerica. Daca acceleratia perturbatoare nu
poate fi exprimata in forma analitica, pentru rezolvarea
problemei se pot aplica metode numerice. In principiu, cu valorile initiale
cum sunt vectorii de pozitie si viteza ![]() si
si ![]() (t),
cunoscuti la o epoca de referinta t, poate fi realizata o integrare
numerica a ecuatiei (30). Acest concept simplu poate fi
imbunatatit prin considerarea elipsei kepleriene ca referinta. Prin aceste mijloace pot fi
integrate doar diferentele mici dintre acceleratia totala
si centrala. Rezultatul integrarii este determinarea cantitatii
diferentiale
(t),
cunoscuti la o epoca de referinta t, poate fi realizata o integrare
numerica a ecuatiei (30). Acest concept simplu poate fi
imbunatatit prin considerarea elipsei kepleriene ca referinta. Prin aceste mijloace pot fi
integrate doar diferentele mici dintre acceleratia totala
si centrala. Rezultatul integrarii este determinarea cantitatii
diferentiale ![]() care, adaugata vectorului de pozitie calculat
cu parametrii elipsei de referinta, da vectorul de pozitie exprimat
functie de elipsa perturbata.
care, adaugata vectorului de pozitie calculat
cu parametrii elipsei de referinta, da vectorul de pozitie exprimat
functie de elipsa perturbata.
In vederea integrarii numerice, ecuatia diferentiala de ordinul doi este de obicei transformata intr-un sistem de doua ecuatii de ordinul intai, al caror aspect este:
 (61)
(61)
Integrarea numerica a acestui sistem poate fi realizata prin aplicarea algoritmului Runge-Kutta care, pe scurt, consta in: Fie y(x) o functie definita in intervalul x1 x x2 ; notam y'=dy/dx, prima sa derivata in raport cu argumentul x. Solutia generala a ecuatiei diferentiale de primul ordin
![]() (62)
(62)
decurge din integrare si o solutie particulara este gasita dupa stabilirea valorii numerice initiale y1=y(x1) drept constanta de integrare. Pentru aplicarea integrarii numerice, in primul rand, intervalul de integrare este subdivizat in n subintervale egale x=(x2-x1)/n si suficient de mici, n fiind un intreg strict pozitiv. Diferenta dintre valorile succesive ale functiei este obtinuta prin mediere ponderata:
![]() , (63)
, (63)
unde :
![]()
![]()
![]()
![]() .
.
Prin urmare, incepand cu o valoare initiala y1 (cea corespunzatoare argumentului x1), functia poate fi calculata pentru argumentul urmator x1+x si asa mai departe.
Metodele numerice pot fi aplicate si pentru integrarea ecuatiilor Lagrange sau Gauss, care dau expresiile perturbatiilor. Acestea au avantajul de a fi ecuatii diferentiale de ordinul intai, deci necesita a fi integrate o singura data in raport cu timpul.
Exemplu de integrare numerica. Consideram o ecuatie diferentiala de ordinul intai y'=y-x+1, cu o valoare initiala y1=1 pentru x1=0. Ne propunem sa rezolvam ecuatia diferentiala pentru argumentul x2=1, cu incrementarea x=0,5. Incepand cu valori initiale pentru primul interval, sunt obtinute succesiv urmatoarele valori: y(1)=1.000, y(2)=1.125, y(3)=1.156 si y(4)=1.328. Media ponderata corespunzatoare va fi y=1,148. Inlocuind in al doilea interval valorile initiale cu x=x1+x=0,5 si y=y1+y=2,148 si procedand intr-o maniera asemanatoare, obtinem y=1,569 si deci rezultatul final va fi y2=y(1)=y+y=2,717. Amintim ca functia y=ex+x, care satisface ecuatia diferentiala initiala, da valoarea adevarata y(1)=2,718. Cu o incrementare x=0,1, integrarea numerica poate furniza o precizie de ordinul 10-6.
4 Precizia orbitelor
1 Retele de urmarire
Obiective si strategii. In prezent, efemeridele transmise au o precizie de pana la 5m pentru satelitii Block I (prevazuti cu ceasuri cu cesiu), pe baza a trei incarcari pe zi. Pentru satelitii Block II, precizia pentru utilizatorii neautorizati poate fi degradata cu o cantitate nespecificata (presupusa a fi intre 30 si 50m), cauzata de cuplarea dispozitivului SA (disponibilitate selectiva). Totusi, in viitorul apropiat, comunitatea geodezica va deveni independenta de politica DOD (Departamentul Apararii SUA), prin punerea la punct a unor retele globale de urmarire a satelitilor GPS.
Retelele globale permit o inalta precizie de determinare a orbitelor, superioara celei obtinuta de retelele regionale. Legatura intre sistemul orbital si sistemul terestru de referinta este realizata de colocatia receptoarelor GPS cu statiile interferometrice si laser. Distributia punctelor GPS este esentiala pentru a obtine cea mai inalta precizie. Pot fi luate in discutie doua situatii posibile:
- distributie uniforma in jurul globului;
- retele mici, dar inconjurate de cate o grupare de puncte aditionale, pentru a imbunatati precizia de determinare a ambiguitatilor, cu scopul declarat de crestere a preciziei parametrilor orbitali cu un factor cuprins intre 3 si 5. Pentru aceasta varianta secunda, sunt necesare aproximativ 20 de zone de urmarire, cu gruparile din jurul lor.
Exemple. Separat de segmentul de control al sistemului GPS, au fost realizate mai multe retele pentru determinarea orbitelor satelitilor. Nu vor fi mentionate aici numeroasele retele la scara regionala sau chiar continentala, fiind date numai cateva exemple de retele globale.
Reteaua GPS de Cooperare Internationala (CIGNET) este realizata de U.S. National Geodetic Survey (NGS), cu statii de urmarire situate in punctele retelei VLBI. In 1991 erau incluse in retea 20 de statii, conform tabelului 5. Douasprezece dintre aceste statii (marcate cu asterix) isi transmit datele de urmarire, in fiecare noapte, la centrul de prelucrare NGS aflat in Rockville, Maryland. NGS prelucreaza datele primite si in dimineata urmatoare transmite catre statii rezultatele, prin intermediul unui File Server Computer. Datele din celelalte statii sunt receptionate de NGS cu o intarziere de 2 la 7 zile si sunt prelucrate si facute disponibile pe parcursul unei zile.
CIGNET este diferita fata de alte retele de urmarire, prin cateva aspecte. In primul (si cel mai important) rand, aceste statii executa determinari atat din faza cat si din cod, pe baza datelor receptionate de la toti satelitii. Deci se determina pseudodistante din cod C/A si cod P pe frecventa L1, pseudodistante din cod P pe frecventa L2, precum si din faza purtatoare pentru ambele frecvente. Cand este cuplat dispozitivul de criptare A-S (anti-spoofing), nu se pot face determinari din codul P. O a doua particularitate a CIGNET este ca datele de urmarire sunt imediat disponibile utilizatorilor, spre deosebire de efemeridele precise oficiale care se distribuie cu cel putin doua saptamani intarziere.
Participantii la programul CIGNET (posibil si altii) pot accesa datele de urmarire si, daca dispun de programe de calcul adecvate, pot sa-si obtina propriile efemeride. O alta modalitate de folosire a datelor de urmarire consta in combinarea cu datele de pozitie culese direct pe teren (prin metode topogeodezice) si folosirea softului de relaxare a orbitei la calculul coordonatelor punctelor locale. NGS a testat aceasta metoda, folosind date de la statiile U.S. CIGNET, obtinand o precizie de cativa centimetri in punctele din mijlocul continentului.
Buletinul GPS realizat si distribuit bilunar de NGS furnizeaza date statistice de urmarire, informatii privind performantele noilor receptoare, perfectionari recente in retea precum si alte imformatii privind CIGNET.
Primul experiment de urmarire globala a orbitelor (GOTEX) a inceput in anul 1988 si a constat in amplasarea statiilor de urmarire GPS la un loc cu cele interferometrice si laser (retelele VLBI, respectiv SLR). Datele trebuia sa permita o conectare stransa intre WGS-84 si sistemele VLBI/SLR. Circa 25 de puncte, distribuite in intreaga lume, au fost stationate pe parcursul unei campanii de trei saptamani. Datele au fost transformate in sistem CIGNET si pot fi obtinute de la NGS.
In 1990, Asociatia Internationala de Geodezie (IAG) a decis sa creeze un Serviciu International Geodinamic (GPS). Dupa o perioada de testare in 1992, activitatile au demarat in 1993. Acest serviciu este dedicat aplicatiilor geodinamice, care necesita o precizie deosebit de ridicata. In paralel se desfasoara si activitati de determinare a orbitelor, similare CIGNET. Reteaua este proiectata sa contina o retea-nucleu permanenta (circa 25 de statii de control) si circa 100 de statii cu activitate intermitenta.
Tabelul 5. Reteaua CIGNET (1991)
|
Statia |
Tara |
|
Hartebeesthoek |
Africa de sud |
|
* Hobart |
Australia |
|
* Kokee Park |
Hawaii, SUA |
|
Madrid |
Spania |
|
* Mojave/Goldston |
California, SUA |
|
Natal |
Brazilia |
|
* Onsala |
Suedia |
|
Port Harcourt |
Nigeria |
|
* Richmond |
Florida, SUA |
|
Santiago |
Chile |
|
Tidbinbilla |
Australia |
|
* Townsville |
Australia |
|
* Tromso |
Norvegia |
|
* Tsukuba-Kashima |
Japonia |
|
Useda |
Japonia |
|
* Wellington |
Noua Zeelanda |
|
* Westford |
Massachusetts, SUA |
|
* Wettzell |
Germania |
|
Yaragadee |
Australia |
|
* Yellowknife |
Canada |
2 Efemeridele
Date de catalog. Scopul datelor de catalog este de a furniza utilizatorilor date mai putin precise, necesare pentru a facilita cautarea satelitilor sau pentru executia graficelor cu vizibilitatea satelitilor GPS. Datele de catalog sunt transmise prin mesaj satelitar (cum se va arata la punctul 5.1.2) si contin in esenta parametrii necesari pentru reprezentarea orbitei, coeficientii pentru evaluarea corectiei de ceas al satelitului si alte cateva informatii (tabelul 6.). Parametrul l da diferenta dintre ascensia dreapta a nodului la epoca ta si timpul sideral Greenwich la epoca t (inceputul saptamanii GPS curente). Reducerea parametrilor keplerieni la epoca observatiilor t se face cu relatiile
 (64)
(64)
in care P reprezinta viteza unghiulara terestra. Ceilalti trei parametri keplerieni a, e, raman neschimbati. Remarcam ca in formula pentru l, al doilea termen din partea dreapta exprima regresia nodului si al treilea termen semnifica modificarea uniforma in timp sideral, incepand cu epoca t. O estimare pentru influenta ceasului satelitului este data de:
![]() . (65)
. (65)
Tabelul 6. Date de catalog
|
Parametrul |
Semnificatia |
|
ID |
Numarul PRN al satelitului |
|
HEALTH |
Starea de functionare a satelitului |
|
WEEK |
Saptamana GPS curenta |
|
ta |
Epoca de referinta, in secunde, in interiorul saptamanii GPS curente |
|
|
Radacina patrata a semiaxei mari a orbitei |
|
e |
Excentricitatea numerica a orbitei |
|
M0 |
Anomalia mijlocie la epoca de referinta |
|
|
Argumentul perigeului |
|
i |
Abaterea de la inclinarea nominala de 55o |
|
l0 |
Longitudinea nodului la inceputul saptamanii |
|
|
Rata ascensiei drepte a nodului |
|
a0 |
Eroarea ceasului (avansul) |
|
a1 |
Eroarea de ceas datorata frecventei |
Efemeridele transmise. Efemeridele transmise de sateliti au la baza observatiile executate in cinci statii de monitorizare, care apartin segmentului de control. Cele mai recente dintre aceste date sunt folosite pentru calculul orbitelor satelitilor. Datele de urmarire aditionale sunt trecute printr-un proces de filtrare Kalman si sunt calculate cele mai probabile orbite pentru perioada urmatoare (prin extrapolare). Aceste date orbitale au o precizie de aproximativ 5 metri, daca se fac trei incarcari pe zi in memoria satelitilor; cu o singura incarcare ne putem astepta la o precizie de 10 metri. Statia principala de control este responsabila cu calculul efemeridelor si incarcarea satelitilor.
In esenta, efemeridele contin sase parametri ce descriu o elipsa kepleriana la o epoca de referinta si cativa termeni de corectie seculara si periodica. Cei mai recenti parametri, 'injectati' de la sol satelitilor, sunt transmisi la fiecare ora, ei trebuind utilizati de-a lungul unei perioade de aproximativ patru ore (pana la o noua 'injectare').
Efectele perturbatoare cauzate de nesfericitatea Pamantului, efectul mareic direct si presiunea radiatiei solare pot fi calculate pe baza ultimilor noua termeni din tabelul 7. Prin urmare, pentru a calcula pozitia satelitului la epoca observatiei, pe langa parametrii a si e sunt necesare urmatoarele cantitati:
 (66)
(66)
in care u=+v reprezinta argumentul satelitului. Distanta geocentrica r0 este calculata cu relatia (7), folosind a,e,E la epoca observatiei. Cu epoca de referinta te se calculeaza l, relatia fiind analoaga cu (64).
Efemeridele precise. Efemeridele precise sunt obtinute pe baza datelor culese in retelele de urmarire si sunt calculate de catre mai multe institutii. Rezultatele nu sunt disponibile pentru utilizatorii neautorizati decat cu cateva saptamani intarziere. Efemeridele precise contin pozitiile satelitului si vitezele la epoci echidistante. Ca un exemplu, se prezinta in continuare formatul NGS, cel mai raspandit in prezent.
Formatul NGS intreg este alcatuit dintr-un header ce contine informatii generale (intervalul epocilor, tipul orbitei etc.) urmat de o sectiune de date pentru
Tabelul 7. Efemeridele transmise
|
Parametru |
Semnificatie |
|
AODE |
Varsta datelor efemeridei |
|
te |
Epoca de referinta a efemeridei |
|
|
Parametrii orbitei Kepleriene la epoca te |
|
n |
Abaterea miscarii mijlocii |
|
i |
Rata unghiului de inclinare |
|
|
Rata ascensiei drepte a nodului ascendent |
|
Cuc,Cus |
Coeficienti de corectie (argumentul perigeului) |
|
Crc,Crs |
Coeficienti de corectie (distanta geocentrica) |
|
Cic,Cis |
Coeficienti de corectie (inclinare) |
epoci succesive. Aceste date sunt raportate pentru
fiecare satelit si reprezinta vectorul de pozitie
geocentrica ![]() [km] si vectorul viteza
[km] si vectorul viteza ![]() [km.s-1].
[km.s-1].
Formatul NGS redus contine doar pozitiile deoarece, in general, viteza este inutila. Viteza poate fi calculata din informatia referitoare la pozitie, cu precizie suficienta, prin diferentiere si interpolare polinomiala. Deci doar jumatate din cantitatea de informatie stocata in formatul intreg este absolut necesara.
Pana in anul 1991, rezultatele NGS se bazau pe distante deduse din cod P, pe ambele frecvente, obtinute din reteaua CIGNET. Ulterior, NGS a trecut la observatii bazate pe analiza fazei. Orbitele sunt calculate utilizand coordonatele statiilor IERS (Serviciul International pentru Rotatia Pamantului), pe care sistemul WGS-84 le aproximeaza. Precizia interna a orbitelor este de ordinul a catorva parti din 10-7. NGS transmite datele ca fisiere ASCII sau fisiere binare. Fisierele binare sunt destinate calculatoarelor personale compatibile IBM, pentru a economisi capacitatea de stocare si a facilita transferul electronic de date. Vectorii de pozitie si viteza intre epocile date sunt obtinuti prin interpolare, fiind preferata interpolarea Lagrange bazata pe functii polinomiale.
Este important faptul ca interpolarea Lagrange este aplicata pentru serii de epoci variabile iar coeficientii determinati pot fi aplicati unor serii de epoci considerabil mai lungi, fara a fi necesara recalcularea lor. Aceasta metoda de interpolare este foarte comoda si pentru faptul ca poate fi programata cu usurinta. Studiile realizate de catre Remondi stabilesc drept suficiente, pentru satelitii GPS, intervalul de 30 minute intre epoci si ordinul 9 de interpolare; se asigura astfel o precizie de aproape 10-8. Un studiu mai recent, realizat tot de Remondi, demonstreza ca utilizand o interpolare de ordinul 17, pentru o precizie de ordinul milimetrilor (10-10) sunt suficiente intervale de 40 minute intre epoci.
Pentru familiarizare cu interpolarea Lagrange, se prezinta in continuare principiul acestei metode si un exemplu numeric.
Se dau epocile tj , j = 0, , n cu valorile functionale asociate f(tj). Deci,
![]() (67)
(67)
este definitia functiilor de baza lj(t) corespunzand gradului n, raportate la o epoca arbitrara t. Valoarea functiei, interpolata la epoca t, rezulta din insumarea:
 . (68)
. (68)
Urmatorul exemplu numeric presupune valorile functiilor f(tj) date la epocile tj:
![]()
Functiile de baza sunt polinoame de gradul II: 
Conform relatiei (68), valoarea interpolata pentru t=4 este f(t)=62. Rezultatul este verificabil imediat, incepand cu generarea valorilor functionale de catre polinomul f(t)=2t2+5t+10.
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
||||||||||
|
||||||||||
Lucrari pe aceeasi tema
| ||||||||||
|
| ||||||||||
|
||||||||||
|
|
||||||||||









