
| Medicina | Medicina veterinara | Muzica | Psihologie | Retete | Sport |
Medicina
|
|
Qdidactic » sanatate & sport » medicina Prelucrarea matematica a datelor experimentale |
Prelucrarea matematica a datelor experimentale
Prelucrarea matematica a datelor experimentale
I. Notiuni teoretice
A. Indicatori de tendinta centrala
Indicatorii de tendinta centrala sunt valori ce localizeaza intr-un fel oarecare mijlocul setului de date. Dintre indicatorii de tendinta centrala mentionam:
Modul - valoarea care apare cel mai frecvent.
Un set de date poate fi non-modal (daca toate valorile posibile au aceeasi frecventa), mono-modal (o singura valoare maximala), multi-modal (cu mai multe valori ce apar cu aceeasi frcventa maximala).
Mijlocul - media aritmetica a valorilor extreme ale setului de date.
Mediana - valoarea ce imparte setul de date in doua grupe egal populate.
Pentru setul de date S=, ordonat crescator, cand n=2k+1 (numar impar de date), mediana este Me=Xk+1. In cazul aceluiasi set dar pentru n=2k (numar par de date), mediana este:
![]()
Media - cele mai folosite sunt: media aritmetica (Xma), geometrica (XG), armonica (XH) si cuadratica (XQ). Se poate arata usor ca aceste medii se afla in relatia:
![]()
B. Indicatori de pozitie
Indicatorii de pozitie sunt folositi pentru localizarea unui anumit subgrup de date in relatie cu restul esantionului. Se numesc a-cuantile acei indicatori ce impart esantionul in parti egal populate. Cele mai utilizate sunt: cvartila (qk), decila si percentila (pk), valori ce impart datele in parti continand o patrime, o zecime, sau o sutime din elemente.
Sa consideram un set de date ordonat crescator unde L este valoarea cea mai mica din set iar H valoarea cea mai mare.
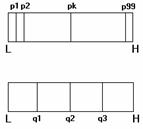
Percentila de ordinul pk este valoarea numerica pentru care k% din date sunt mai mici decat pk iar (100-k)% sunt mai mari. Se observa ca p50 = q2.
C. Indicatori de imprastiere (dispersie)
Indicatorii de imprastiere descriu variabilitatea datelor. Datele grupate strans au valori mici pentru indicatorii de dispersie, in timp ce datele imprastiate au valori mari.
Principalii indicatori de imprastiere sunt: domeniul, varianta, deviatia si momentele.
Domeniul - reprezinta intervalul de valori al datelor.
D=[Xmin, Xmax]
Uneori se indica largimea domeniului (amplitudinea imprastierii):
Dx= Xmax - Xmin
Toate deviatiile medii fata de un indicator de tendinta centrala (media aritmetica, geometrica, cuadratica, armonica sau modul, mediana, notate generic prin <x>) se definesc in acelasi fel, ca medii ale diferentei intre valoarea masurata si indicatorul respectiv.
Mai general este momentul centrat de ordin q, mq(x) fata de media x. In continuare vom analiza semnificatia si utilitatea unora dintre momentele centrate:
- m1(x)=0, momentul centrat de ordinul 1, nu aduce nici o informatie, intrucat ia valoarea zero oricare ar fi distributia datelor; din aceasta cauza nu este folosit.
- m2(x) se numeste varianta (V); radacina patrata a variantei se numeste deviatie patratica, notata cu s. Ambele marimi arata imprastierea datelor.
Orice rezultat experimental trebuie prezentat prin media aritmetica deviatia. Intervalul (<x>-s, <x>+s se numeste interval de incredere sau confidenta.
Intrucat in biologie si medicina sunt in general putine date de procesat, trebuie sa se inlocuiasca varianta V cu varianta standard SV si deviatia sn cu deviatie standard sn-1 sau SD (se utilizeaza indicatorii standard sn-1 si SV cand n<30, adica setul are mai putin de 30 de valori).
- m3(x) este numit inclinare sau oblicitate si se utilizeaza la definirea coeficientului de asimetrie, ac (numit in engleza skewness si notat SKEW)
|
![]()
Functie de valorile acestui coeficient exista trei tipuri de distributii: cu inclinare pozitiva, nula si negativa, asa cum reiese din cazurile prezentate mai jos, unde Mo=modul, Me=mediana, <x>=media.
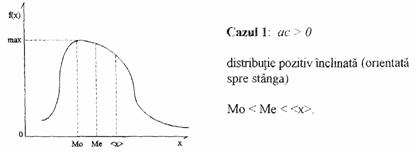

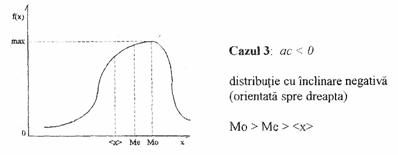
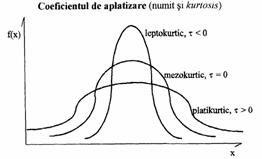
- m4(x) se numeste exces si arata cat de aplatizata este distributia. Se foloseste la definirea coeficientului de aplatizare sau boltire, t (numit in engleza kurtosis, notat prin KURT):
![]()
II. Parte experimentala
A. Determinarea intervalului de confidenta
Sa presupunem ca in urma unui experiment se obtin "n" date experimentale: x1, x2, ., xn. Pentru acest set de date putem defini urmatoarele valori:
- media
aritmetica: ![]()
-
eroarea absoluta: ![]()
-
deviatia standard: ![]()
Rezultatul determinarilor (R) in urma prelucrarilor statistice a datelor, se prezinta sub forma:
![]()
Dupa efectuarea acestor calcule, putem trage concluzia ca valoarea reala X a marimii catuate se afla in intervalul:
![]()
Acest interval se numeste interval de confidenta sau interval de incredere.
Problema: Pentru etalonarea unui colorimetru s-au realizat un numar de n = 5 determinari, iar valorile transmisiei au fost urmatoarele: 50.2, 49.1, 49.6, 50.3, 48.9. Sa se calculeze rezultatul determinarilor (R) si intervalul de confidenta (I).
B. Reprezentarea grafica a datelor
Procesele fizice, chimice, biologice, etc., procese ce depind de mai multi parametrii, pot fi reprezentate folosind un sistem de referinta format din doua drepte concurente in plan, sau trei drepte concurente in spatiu, numite axe. Daca axele sunt perpendiculare cate doua, atunci sistemul se numeste rectangular.
Coordonatele (xa, ya) ale unui punct A intr-un sitem rectangular avand originea O masoara proiectiile segmentului OA pe axa.
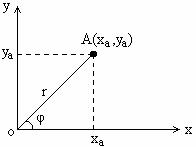
Figura 1.1. Legatura dintre sistemul de referinta rectangular si cel polar.
In practica se mai utilizeaza si sistemul de coordonate polare. In acest caz coordonatele punctului A se definesc prin marimile: r = OA (raza polara) si unghiul φ dintre OA si axa OX. Aceasta reprezentare se utilizeaza in momentul cand functia reprezentata depinde de unghi.
Legatura intre cele doua sisteme de coordonate este urmatoarea:
![]() ,
, ![]()
![]() ,
, ![]()
Pentru ca reprezentarea grafica a datelor in coordonate rectangulare sa fie cat mai clara, se recomanda sa se tina cont de urmatoatele indicatii:
-asigurarea unei reprezentari grafice cat mai intuitive consta in alegerea scarii corespunzatoare atat pe scara absciselor cat si pe scara ordonatelor (atunci cand valorile variabilelor x sau y incep de la un numar oarecare, acest numar se recomanda sa fie reprezentat cat mai aproape de originea axei respective).
-indicatiile de pe axele x si y trebuie sa fie cat mai simple, adica cu cat mai putine cifre (de regula indicatiile de pe axe nu trebuie sa contina numere cu mai mult de doua cifre; daca numerele sunt mai mari trebuie indicat un factor de multiplicare la sfarsitul axei alaturi de unitatile de masura).
-pe fiecare axa trebuie sa se indice denumirea sau simbolul marimii reprezentate pe axa respectiva si in mod obligatoriu unitatile de masura.
Sa urmarim in continuare un exemplu simplu: presupunem ca la anumite intervale de timp masuram temperatura unui bolnav (datele obtinute se regasesc in tabelul de mai jos) si dorim sa reprezentam grafic acest proces: temperatura = f (timp).
Tabelul 1
|
Timp (ore) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Temp. (C0) |
37,1 |
37,5 |
37,9 |
38 |
38,2 |
38,4 |
38,8 |
39 |
39,2 |
39,5 |
Tinand cont de precizarile de mai sus se traseaza graficul prin puncte (dar fara a le uni), avand grija sa reprezentam numai zona de interes (figura 1.2).
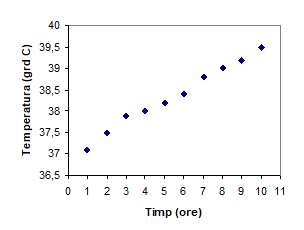
Figura 1.2. Reprezentarea grafica a datelor din tabelul 1.
Privind graficul de mai sus, ne putem pune urmatoarea intrebare: care este valoarea de temperatura a pacientului la un moment de timp la care nu a fost facuta masuratoarea efectiva?
In
aceasta situatie suntem nevoiti sa determinam, pornind
de la datele noastre, "curba ce se
potriveste" cel mai bine cu punctele experi-mentale. In cazul graficului
reprezentat in figura 1.2, putem presupune o dependenta de tip liniar:
![]() , unde coeficientii
, unde coeficientii ![]() sunt necunoscute.
sunt necunoscute.
Cea mai simpla varianta de determinare a coeficientilor, o ofera programul de calcul tabelar Microsoft Excel.
Dupa introducerea datelor in foaia de lucru si trasarea graficului se utilizeaza optiunea Insert Trendline. Din fereastra de dialog (figura 1.3) se alege de la grupul Type tipul de Trend dorit (in cazul nostru liniar), iar de la grupul Options se selecteaza Display Equation on Chart. Rezultatul este prezentat in figura 1.4.

Figura 1.3. Fereastra de dialog "Format Trendline" a programului Microsoft Excel.
Facem mentiunea ca utilizatorul este lasat sa aleaga, tinand cont de distributia punctelor, tipul functiei cu care urmeaza sa fie facuta fittarea: liniara, logaritmica, exponentiala, putere si polinomiala (pana la gradul 6).
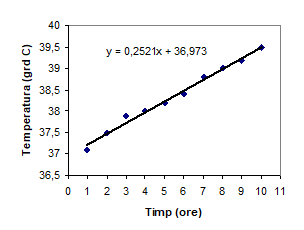
Figura 1.4. Determinarea coeficientilor a0 si a1 cu ajutorul programului Microsoft Excel.
Revenind la exemplul nostru, rezultatul este:
![]()
Asa cum se poate vedea din graficul prezentat in figura 1.4, punctele experimentale sunt apropiate de dreapa trasata. In cazul in care exista puncte departate de drepta, atunci in acea regiune putem avea o alta dependenta si este necesar reluarea procedeului cu alegerea unui trend adecvat.
Problema: Sa se reprezinte grafic datele din tabelul de mai jos y=f(x) si apoi utilizand programul Microsoft Excel sa se traseze "curba ce se potriveste" cel mai bine cu punctele experimentale.
|
x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
y |
37.1 |
37.5 |
37.9 |
38.33 |
38.4 |
38.4 |
38.2 |
37.85 |
37.43 |
36.93 |
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2026 - Toate drepturile rezervate -| |
|
|
|||
|
|||
|
|||
Esee pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








