
| Afaceri | Agricultura | Comunicare | Constructii | Contabilitate | Contracte |
| Economie | Finante | Management | Marketing | Transporturi |
Electrica
|
|
Qdidactic » bani & cariera » constructii » electrica Puteri in curent alternativ |
Puteri in curent alternativ
Puteri in curent alternativ
 i = Im sin
ωt
i = Im sin
ωt
u = Um sin (ωt + φ)
p = u i = Um Im sin (ωt + φ) sin ωt = 2 U I sin ωt sin (ωt + φ)
p = U I [cos φ – cos(2ωt + φ )]
In Fig. 3.9.2 am reprezentat variatia marimilor u, i si p defazajul curentului fata de tensiune fiind de 600.
Valoarea medie a puterii este :
Pmed = P = ![]()
Aceasta valoare se numeste putere activa:
P = U I cos φ, [W]
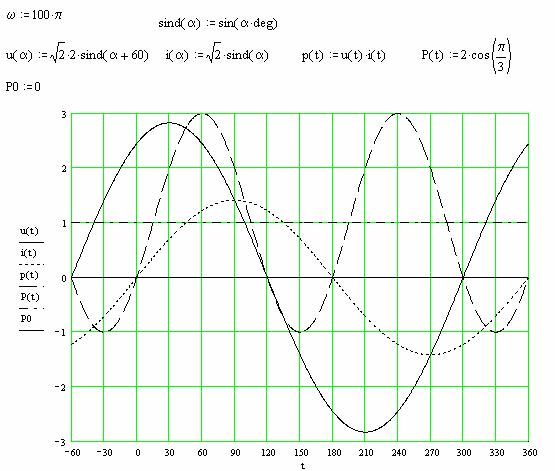 Fig. 3.9.2
Fig. 3.9.2
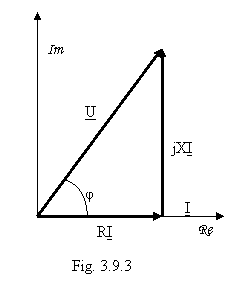 Diagrama fazoriala a consumatorului
considerat este aceea prezentata in figura 3.9.3
Diagrama fazoriala a consumatorului
considerat este aceea prezentata in figura 3.9.3
P = U I cos φ = R I2
rezistenta in curent alternativ prin formula:
![]()
Se numeste factor de putere raportul dintre puterea activa si produsul dintre U si I:
![]()
Produsul dintre valorile efective ale curentului si tensiunii se numeste putere aparenta si se noteaza cu S:
S = U I [VA]
Se numeste putere reactiva marimea:
Q = U I sin φ [VAr]
Puterea reactiva se mai poate calcula cu expresia: Q = X I2
Integrala in functie de timp a puterii active poarta numele de energie activa:
![]() [Ws, kWh]
[Ws, kWh]
Integrala in functie de timp a puterii reactive poarta numele de energie reactiva si se masoara in [VArh].
S2 = P2 + Q2
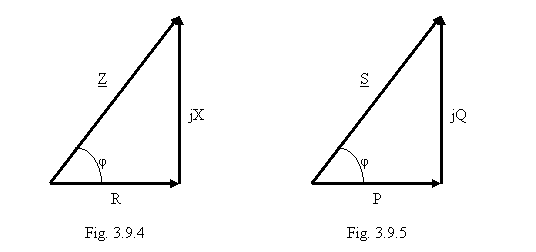
Prin imparttirea fazorilor din diagrama fazoriala din figura 3.9.3 la I se obtine diagrama din figura 3.9.4 care poarta numele de triunghiul impedantelor. In acest triunghi pentru un consumator inductiv fazorul impedantei Z este defazat cu unghiul φ inaintea lui R. Pentru consumatori capacitivi fazorul impedantei Z este defazat in urma axei reale cu unghiul φ.
Se defineste puterea complexa S prin relatia:
S = U I*
unde I* este complex conjugatul fazorului I. Pentru cazul consumatorului considerat avem:
S = U I* = U ejφ I = U I ejφ = S ejφ = U I cos φ + j U I sin φ = P + j Q = R I2 + j X I2
Daca se inmultesc fazorii din diagrama tensiunilor (Fig. 3.9.3) cu complex conjugatul curentului I* se
obtine triunghiul puterilor din figura 3.9.5.
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||||||
|
|||||||
|
|||||||
Documente online pe aceeasi tema | |||||||
|
| |||||||
|
|||||||
|
|
|||||||








