
| Aeronautica | Comunicatii | Drept | Informatica | Nutritie | Sociologie |
| Tehnica mecanica |
Informatica
|
|
Qdidactic » stiinta & tehnica » informatica Liniarizarea sistemelor neliniare |
Liniarizarea sistemelor neliniare
Liniarizarea sistemelor neliniare
Cele mai multe componente ale sistemelor fizice au caracteristici neliniare. In pratica anumite caracteristici neliniare pot fi aproximate cu modele liniare pe un domeniu larg de functionare. Exista si componente fizice cu caracteristici puternic neliniare pentru care un model liniar este valabil doar intr-un domeniu limitat de functionare, deseori doar in punctual de functionare in care este realizata liniarizarea. In multe cazuri, cand un sistem neliniar este liniarizat intr-un punct de functionare, modelul liniar poate contine elemente variabile in timp.
Fie un sistem neliniar reprezentat de urmatoarea ecuatie de stare
![]()
unde x(t) este vectorul de stare de dimensiune n, u(t) este vectorul intrarilor de dimensiune p, iar f este o functie vectoriala de dimensiune n.
Deoarece sistemele neliniare sunt de regula greu de analizat si proiectat, este de dorit sa se efectueze o liniarizare cand este posibil.
Liniarizarea se face prin dezvoltarea in serie Taylor in jurul unui punct nominal de functionare sau a unei traiectorii nominale. Sunt neglijati toti termenii de ordin mai mare ca unu si rezulta o aproximare liniara in punctual nominal de functionare.
Fie traiectoria nominala de functionare x0(t) ce corespunde intrarii nominale u0(t) si anumitor conditii initiale fixate. Dezvoltam ecuatia de stare neliniara in serie Taylor in jurul lui x0(t), neglijam termenii de ordin superior si obtinem
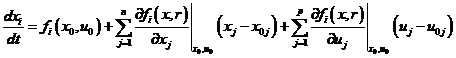
unde i = 1, 2, ., n. Fie
![]()
si
![]()
Atunci
![]()
Deoarece
![]()
ecuatia liniarizata se scrie

Ecuatia se poate scrie sub forma matricial-vectoriala
![]()
unde


Mentionam ca matricele A si B au fost evaluate in punctul nominal de functionare x0, u0. Matricele A si B pot contine elemente variabile in timp.
|
Exemplu. Fie sistemul neliniar cu neliniaritatea saturatie din Figura 45.

Figura 45 . Sistem neliniar.
Ecuatiile de stare ale partii liniare sunt
![]()
![]()
Saturatia este descrisa de ecuatia intrare - iesire
![]()
unde
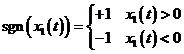
Ecuatiile liniarizate sunt
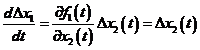
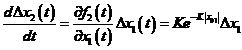
unde x01 este valoarea nominala a lui x1(t). Ecuatiile liniarizate sunt valabile doar pentru semnale mici. In forma matricial-vectoriala, ecuatiile de stare liniarizate se scriu
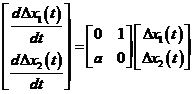
unde
![]()
Este interesant de vazut semnificatia liniarizarii. Daca x01 este ales in originea neliniaritatii, x01 = 0, atunci a = K si ecuatia liniarizata devine
![]()
In acest caz modelul
liniarizat este echivalent cu inmultirea cu constanta K. Pe de alta
parte, daca x01 este mare, punctual nominal de functionare
va fi pe portiunea saturata a neliniaritatii si a = 0.
Asta inseamna ca orice mica variatie a lui x1(t)
(si deci a lui ![]() ) nu va produce practic nicio schimbare in
) nu va produce practic nicio schimbare in ![]() .
.
Exemplu. Fie sistemul neliniar
![]()
![]()
Vom liniariza aceste ecuatii in jurul traiectoriei nominale [x01(t), x02(t)] care este solutia ecuatiilor diferentiale cu conditiile initiale x1(0) = x2(0) = 1 si intrarea u(t) = 0.
Solutia nominala a ecuatiilor este:
x02(t) = x2(0) = 1
x01(t) = -t + 1
Vom calcula elementele matricelor A si B de mai sus.
 ,
, 
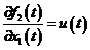 ,
, 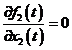
 ,
, 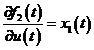
Ecuatiile liniarizate sunt
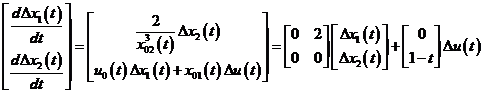
Aceasta ecuatie are un coeficient variabil in timp.
Exemplu. Fie sistemul de suspensie magnetica a unui bile din Figura 46. Sistemul trebuie sa mentina pozitia bilei prin modificarea curentului in electromagnet prin intermediul tensiunii de intrare e(t).
Ecuatiile ce descriu sistemul sunt:
![]()
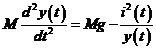
In ecuatiile de mai sus M este masa bilei, g acceleratia gravitationala, y(t) este pozitia bilei, L si R sunt inductanta si respective rezistenta infasurarii, i(t) este curentul prin infasurare, iar e(t) este tensiunea de intrare. Forta dezvoltata de electromagnet este indreptata in sensul descresterii distantei, adica este o forta de atractie.
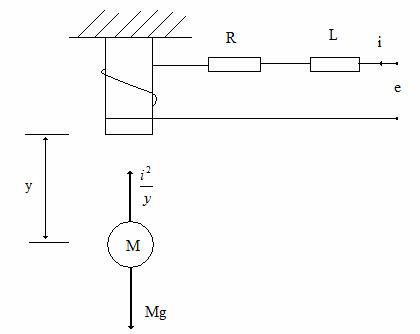
Figura 46 . Sistem de suspensie magnetica a unei bile.
Vom rescrie sistemul de
ecuatii sub forma unui sistem de ordinul intai cu notatiile ![]() ,
, ![]() ,
, ![]() . Ecuatiile de stare sunt
. Ecuatiile de stare sunt
![]()
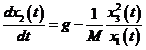
![]()
Vom liniariza sistemul de
ecuatii in jurul punctului de echilibru ![]() . Avem deci
. Avem deci
![]()
![]()
Valoarea nominala a curentului se determina din ecuatia de miscare a bilei
![]()
Ecuatiile de stare liniarizate au matricele A si B de mai jos:


| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2026 - Toate drepturile rezervate -| |
|
|
||||||||||||||||||||||||
|
||||||||||||||||||||||||
|
||||||||||||||||||||||||
Documente online pe aceeasi tema | ||||||||||||||||||||||||
|
| ||||||||||||||||||||||||
|
||||||||||||||||||||||||
|
|
||||||||||||||||||||||||








