
| Aeronautica | Comunicatii | Drept | Informatica | Nutritie | Sociologie |
| Tehnica mecanica |
Informatica
|
|
Qdidactic » stiinta & tehnica » informatica Ecuatiile sistemelor mecanice |
Ecuatiile sistemelor mecanice
Ecuatiile sistemelor mecanice
Ecuatiile sistemelor mecanice se scriu construind un model al sistemului cu elementele interconectate. Metoda de deducere a ecuatiilor este urmatoarea:
se presupun deplasari si directii de deplasare arbitrare pentru fiecare corp din sistem. Deplasarile sunt variabile dependente, (iesiri), iar fortele sunt marimile de actionare (intrari). Se persupune ca deplasarea, viteza si acceleratia au acelasi sens,
se aplica legea lui Newton si se scie cate o ecuatie pentru fiecare corp. Pentru a depista fortele ce actioneaza asupra fiecarui corp, se utilizeaza diagrama corpului liber,
se aplica transformata Laplace asupra ecuatiilor rezultate si se obtine un sistem de ecuatii algebrice care se rezolva.
Exemplu. Fie sistemul masa-resort-frecare din Figura 39.

Figura 39 . Sistem masa-resort-frecare.
Diagrama corpului liber este cea din Figura 40.

|
x"=x'+a', y"=y'+b'.
Trecerea de la M(x,y) la M"(x",y") se va exprima prin:
x"=x+(a+a'), y"=y+(b+b'),
adica produsul a doua translatii este tot o translatie.
In
concluzie, translatiile plane formeaza un grup G, cu doi parametri.
Vom observa ca nici-un produs al matricei generale ![]() nu ne permite sa
gasim relatiile (1.17). Pentru rezolvarea situatiei se va
introduce o a treia componenta a vectorilor (x y) si (x' y'),
obtinand (x y 1) si (x' y' 1). Matricea transformarilor
va fi obligatoriu de 3x2:
nu ne permite sa
gasim relatiile (1.17). Pentru rezolvarea situatiei se va
introduce o a treia componenta a vectorilor (x y) si (x' y'),
obtinand (x y 1) si (x' y' 1). Matricea transformarilor
va fi obligatoriu de 3x2:  . Vom arata ca ea furnizeaza bine o
translatie::
. Vom arata ca ea furnizeaza bine o
translatie::

sau : x'=x+a, y'=y+b, unde a produce o translatie pe axa Ox si b pe axa Oy.
Problema translatiei pare a fi rezolvata. Dar o matrice 3x2 nu poseda inversa. De aceea se mai adauga o coloana.
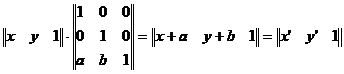
Spunem ca reprezentarea pozitiei unui punct printr-un vector cu trei componente este o reprezentare in coordonate omogene.
Figura 40 . Diagrama corpului liber.
Ecuatia ce descrie miscarea corpului este
![]()
Vom pune aceasta ecuatie sub forma ecuatiilor de stare cu substitutiile
y = x1
y' = x2
Ecuatiile de stare sunt
![]()
![]()
Functia de transfer intre Y(s) si F(s) este

| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
||||||||||||||||||||||||
|
||||||||||||||||||||||||
|
||||||||||||||||||||||||
Esee pe aceeasi tema | ||||||||||||||||||||||||
|
| ||||||||||||||||||||||||
|
||||||||||||||||||||||||
|
|
||||||||||||||||||||||||








