
| Biologie | Botanica | Chimie | Didactica | Fizica | Geografie |
| Gradinita | Literatura | Matematica |
Matematica
|
|
Qdidactic » didactica & scoala » matematica Interpolarea si aproximarea datelor |
Interpolarea si aproximarea datelor
INTERPOLAREA SI APROXIMAREA DATELOR
1. OBIECTIVELE LUCRARII
Studiul metodelor de aproximare a datelor prin regresie liniara si polinomiala;
Studiul metodelor de interpolare liniara prin metoda transformatei Fourier.
2. BREVIAR TEORETIC
Se propune urmatoarea strategie de aproximare: mai intai, aproximarea unui set de date printr-o linie dreapta (regresie liniara), apoi prin aproximarea printr-un polinom (regresie polinomiala).
Pentru ca aproximarea sa fie considerata foarte buna, suma patratelor distantelor de la fiecare punct la curba aproximata (linie sau polinom) trebuie sa fie minima. Cu aceasta conditie indeplinita, este posibil ca nici un punct al setului de date sa nu se gaseasca pe curba aproximanta,
ceea ce reprezinta diferenta fata de interpolare, la care toate punctele sunt situate pe curba.
2.1. Regresie liniara
Regresia liniara aproximeaza setul de date printr-o dependenta liniara care minimizeaza suma patratelor dintre dreapta de aproximare si punctele date.
Masura calitatii unei aproximari liniare, data de suma patratelor distantelor de la fiecare punct la estimatia liniara, este exprimata prin
sum p= sum ((y-y1). 2) (7.1)
Determinarea parametrilor m si n ai dreptei de aproximare y = mx+n se face folosind functia polyfit.
Exemplul 1
Sa se aproximeze in sensul CMMP cu o regresie liniara setul de date:
x=[0,1,2,3,4,5
y=[0,20,60,68,77,100
Secventa MATLAB care realizeaza aceasta aproximare este prezentata in continuare.
x=[0,1,2,3,4,5
y=[0,20,60,68,77,100
coef=polyfit(x,y,1);
m=coef(1);
n=coef(2);
y1=m*x n;
sump=sum((y-y1). 2)
axis([-1,6,-20,120
plot(x,y1,x,y, 0
grid on
Interpretati reprezentarea grafica obtinuta.
2.2. Regresie polinomiala
Regresia polinomiala realizeaza aproximarea setului de date printr-un polinom de forma
p(x)=![]() =a0xN+ a1xN - 1 +
+aN-1x+aN (7.2)
=a0xN+ a1xN - 1 +
+aN-1x+aN (7.2)
Coeficientii a0,a1,aN ai polinomului de regresie sunt calculati cu ajutorul metodei CMMP, ceea ce presupune minimizarea functiei obiectiv
![]() (7.3)
(7.3)
Algoritmul regresiei polinomiale cuprinde urmatoarele etape:
1. Calculul sumelor in xi si yi
 (7.4)
(7.4)
2. Calculul polinomului de regresie de grad n.
3. Generarea matricii sistemului de ecuatii, a termenului liber si rezolvarea sistemului de ecuatii liniare
|
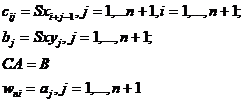 (7.5)
(7.5)
4. Calculul dispersiei si a abaterii standard
 (7.6)
(7.6)
5. Testarea gradului polinomului de regresie in vederea validarii lui
![]() n<nmax
n<nmax![]() n=n+1 si salt la 3;
n=n+1 si salt la 3;
n>nmax![]() salt la 6.
salt la 6.
6. Determinarea gradului optim j al polinomului de regresie
min (gradj, j=1,.,nmax)
j
Daca setul de date are N elemente, toate datele se afla pe curba de aproximare. Pentru un polinom avand gradul mai mic decat numarul de date, aproximarea este cu atat mai buna cu cat gradul polinomului este mai apropiat de numarul de date. Utilizarea unui polinom de aproximare de grad mai mare decat setul de date poate conduce la erori de aproximare considerabile.
Determinarea celei mai bune aproximari a unui set de date (x,y) cu un polinom de ordinul n se face folosind functia polyfit, cu sintaxa
p=polyfit(x,y,n)
care returneaza coeficientii ai ai polinomului p(x) caracterizat de proprietatea ca prezinta, in punctele precizate de vectorul x, valorile date de vectorul y (in sensul CMMP).
Exemplul 2
Fie polinomul p(x)=x3-6x2+11x-6, peste care este suprapus un zgomot cu distributie normala. Aproximati in sensul CMMP datele rezultate cu un polinom de grad 3. Reprezentati grafic datele cu zgomot si polinomul aproximant.
Secventa de program MATLAB este
p= 1,-6,11,-6
x=0:.25:4;
y=polyval(p,x)+rand n(size(x));
c=polyfit(x,y,3);
poli3=polyval(c,x);
plot(x,poli3,x,y, 0
grid on
Obs. Functia polyval(p,s) evalueaza polinomul definit de vectorul p, al coeficientilor polinomiali, in punctul s.
2.3.Interpolarea functiilor de o singura variabila
2.3.1. Interpolarea prin metoda transformatei Fourier
Functia interpft interpoleaza datele cu o singura variabila utilizand metoda FFT si se apeleaza cu sintaxa
y=interpft(x,n)
care returneaza un vector y de lungime n obtinut din vectorul x. Numarul n trebuie sa fie mai mare decat numarul de elemente al vectorului x, iar rezultatul are o periodicitate circulara data de utilizarea transformatei Fourier.
Exemplul 3
Fie datele obtinute dintr-un sinus esantionat cu 8 pasi pe perioada
y=![]() (7.7)
(7.7)
Interpolati datele cu un pas dublu si verificati valorile obtinute cu secventa MATLAB.
k=0:7;
x=sin(2*pi*k/8);
yi=interpft(x,16);
k1=0:15;
yr=sin(2*pi*k1/16);
d=max(yi-yr);
Rezultatul obtinut este
d=5.5511e-0,16
Diferenta maxima intre valorile interpolate si cele reale este egala cu ordinul de marime al celui mai mic numar reprezentabil in calculator (eroarea de trunchiere).
2.3.2.Interpolarea liniara
Daca se presupune ca functia dintre doua puncte de coordonate (x1, y1), respectiv (x2, y2), poate fi estimata printr-o linie dreapta, atunci
valoarea functiei in orice punct x dintre cele doua valori se deduce cu expresia
f(x)=![]() (7.8)
(7.8)
Interpolarea liniara a functiilor de o singura variabila se face cu functia tabel care se apeleaza cu sintaxa
y=tabel(nume_tabel,x)
Primul argument al functiei este numele tabelului care contine datele ce se refera la coordonatele (xi,yi). Daca acesta este un fisier pe disc, atunci nume_fisier trebuie sa fie mai intai incarcat cu functia load.
Al doilea argument se refera la valorile lui x pentru care se doreste determinarea valorilor interpolate y.
Datele din prima coloana a tabelului (valorile lui x) trebuie sa fie in ordine crescatoare, iar valorile x trebuie sa se gaseasca intre prima si ultima valoare a primei coloane; in caz contrar, se afiseaza un mesaj de eroare.
Daca tabelul din care se citesc datele contine mai mult de doua coloane, functia tabel returneaza un vector linie cu N-1 elemente, unde N este numarul de coloane ale tabelului. Fiecare valoare returnata este interpolata din coloana corespunzatoare a datelor.
Exemplul 4.
Estimati valorile temperaturii la momentele de timp 2.5 sec si 4.9 sec, cu datele urmatoare:
0.0 C .. 0.0 s
20.0 C .. 1.0 s
60.0 C .. 2.0 s
68.0 C .. 3.0 s
77.0 C .. 4.0 s
110.0 C ..5.0 s
Se introduc datele intr-o matrice care are in prima coloana valorile timpului si in a doua coloana temperaturile corespunzatoare:
temp1(:,1)= 0.0,1.0,2.0,3.0,4.0,5.0
temp1(:,2)= 0.0,20.0,60.0,68.0,77.0,110.0
Cu instructiunea
y=tabel(temp1,[2.5 4.9
se obtin rezultatele
y=[64.0 107.0
3. MODUL DE LUCRU. PROBLEME PROPUSE
Daca nu este deja creat, se creeaza un director/folder de lucru.
Se activeaza platforma MATLAB si se introduc secventele de program prezentate in exemplele din cuprinsul Breviarului teoretic, urmarindu-se indeplinirea cerintelor enuntate la fiecare dintre ele.
Se considera un traductor de debit cu diafragma. Setul de date experimentale obtinute pentru trasarea caracteristicii statice, si anume marimea de intrare - debitul volumic - si marimea de iesire - curentul generat de traductor - sunt urmatoarele:
10,14 m3/h..........10 mA
8,64 m3/h ..........8 mA
7,20 m3/h...........6 mA
4,5 m3/h..........3,5 mA
2 m3/h...........2,5 mA
1,5 m3/h...........2,2 mA
0,1 m3/h...........2 mA
Se cere aproximarea setului de date printr-un polinom de forma prezentata in relatia (7.2), pe baza algoritmului de la paragraful 2.2.
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||
|
|||
|
|||
Esee pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








